Научный журнал

Научное обозрение. Педагогические науки

ISSN 2500-3402

ПИ №ФС77-57475

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Медведев С.Ю. 1 Козинов Е.И. 1 Курносов В.Е. 1

---

1 Пензенский государственный технологический университет

Предложена дискретно-непрерывная модель, создан программный комплекс для исследования динамических характеристик узлов на печатных платах электронной аппаратуры и приборов. Математическая модель отличается дискретным представлением собственных форм и аналитическим представлением функции времени. Разработан способ описания конструкции и способ задания внешних механических воздействий. Приведены результаты решения задач вычисления собственных форм и частот колебаний методом итераций. Допускаются различные способы закрепления узла на печатной плате. Вычисляются функции прогиба, ускорения, механические напряжения. Для решения дифференциального уравнения используется метод конечных разностей. Получены конечно-разностные выражения для дифференциального оператора. Собственные формы имеют дискретное представление. Функция времени представлена в аналитической форме. Система уравнений формируется по исходным данным и по графическому представлению конструкции. Выполняется оценка сходимости решения при вычислении собственных форм и частот. Имеется возможность визуализации колебаний печатной платы при ударных и вибрационных воздействиях. На заключительном этапе выполняется развертка во времени функций, характеризующих реакцию печатного узла на заданные воздействия. Разработанная модель исследования динамики пластинчатых конструкций, позволяет учитывать установленное количество собственных форм и частот. Это дает возможность исследовать реакцию узлов на печатных платах в заданном частотном диапазоне.

Статья в формате PDF

648 KB

формы колебаний

собственные частоты

обеспечение виброустойчивости

дискретно-непрерывное моделирование

пластинчатые конструкции

узлы на печатных платах

1. Бидерман В.Л. Механика тонкостенных конструкций. Статика. – М.: Машиностроение, 1977. – 488 с.

2. Курносов В.Е. Информационное обеспечение проектирования узлов на печатных платах на основе дискретно-непрерывного моделирования / Т.В. Андреева // Обработка информации: методы и системы: Сборник научных статей. – М.: Горячая линия – Телеком, 2003. – С. 130 – 137.

3. Курносов В.Е. Программный комплекс исследования динамики пластинчатых конструкций электронной аппаратуры в широком частотном диапазоне на основе дискретно-непрерывной модели / Т.В. Андреева, В.Е. Курносов // ХХI век: итоги прошлого и проблемы настоящего плюс: Периодическое научное издание. – Пенза: Изд-во Пенз. гос. технол. ун-та, 2013. – № 10(14). – С 215 – 221.

4. Говоренко Г.С. Теоретические аспекты построения информационной технологии моделирования вибраций конструкций РЭА для оценки ее надежности/ Г.С. Говоренко, В.Е. Курносов, В.А. Ушаков, К.Ю. Парфенов // Надежность и качество 2002: Сб. докладов международного симпозиума. – Пенза: Изд-во Пенз гос ун-та, 2002. – C. 47-52.

5. Говоренко Г.С. Система моделирования динамики конструкций электронной аппаратуры / Г.С. Говоренко, В.Е. Курносов, В.А. Ушаков, К.Ю. Парфенов // Надежность и качество 2002: Сб. докладов международного симпозиума. – Пенза: Изд-во Пенз гос ун-та, 2002. – C. 53-58.

6. Курносов В.Е. Логико-математические модели в задачах проектирования электронной аппаратуры и приборов: Монография / В.Е. Курносов, В.И. Волчихин, В.Г. Покровский. – Пенза: Изд-во Пенз. гос. технол. ун-та, 2016. – 148 с.

Совершенствование математических моделей, расширение возможностей математического моделирования позволяет принимать обоснованные решения на этапе проектирования. К наиболее сложной проблеме проектирования относится проблема обеспечения надежности конструкций при механических воздействиях. Для обеспечения возможности исследования динамики узлов на печатных платах на основе моделирования необходимо решение следующих задач:

– построение математической модели, позволяющей получить адекватное решение;

– разработка способа описания конструкции и задания внешних воздействий для обеспечения возможности исследования реакции конструкции на заданные воздействия по результатам моделирования, их использование для обоснования проектных решений;

– интерпретация и обработка результатов решений, представленных результатами исследования колебаний. Процесс характеризуется значениями функций координат и времени: прогиба, ускорения, механических напряжений и других.

Предлагается дискретно-непрерывная математическая модель, позволяющая исследовать колебания узла на печатной плате в широком частотном диапазоне.

Печатный узел рассматривается как изотропная пластина постоянной толщины с неоднородным распределением плотности материала, что позволяет учесть массу установленных элементов, существенно влияющих на резонансные частоты, амплитуду колебаний и механические напряжения в элементах конструкции.

Прогиб W срединной поверхности пластины при статической распределенной нагрузке q дает решение уравнения 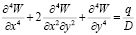[1]:

, (1)

где 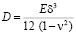– цилиндрическая жесткость пластины; E – модуль Юнга; δ – толщина пластины; ν – коэффициент Пуассона.

Функция перемещения креплений пластины 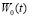задана. Тогда выражение для инерционных сил

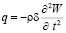. (2)

Плотность материала есть функция координат 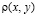, что позволяет учесть массу навесных элементов. С учетом потерь энергии на внутреннее трение уравнение (1) принимает вид:

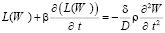. (3)

Здесь 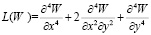– дифференциальный оператор; b – коэффициент вязкости материала платы.

На основе выражения (3) рассмотрим построение модели печатного узла [2, 3]. С учетом прогиба 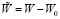относительно закрепленных областей платы получим:

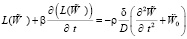(4)

Для получения решения уравнение (4) необходимо дополнить начальными и граничными условиями. Граничные условия зависят от способа закрепления печатного узла:

– для жестко защемленных областей пластины:

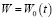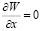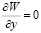; ; . (5)

– для шарнирного крепления:

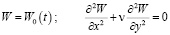. (6)

– для незакрепленных областей, по внешнему контуру пластины:

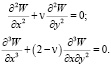(7)

Начальные условия зададим в виде:

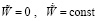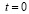при . (8)

Для дискретно-непрерывной модели выражение для прогиба имеет вид:

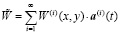. (9)

Здесь 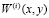– собственные формы колебаний:

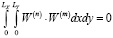при 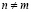. (10)

После подстановки выражения для прогиба (9) в уравнение (4), с учетом ортогональности собственных форм колебаний, получим:

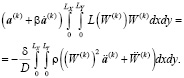(11)

Здесь 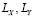– размеры узла на печатной плате. В случае, когда собственная форма 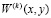определена, воздействие 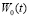задано, функцию времени 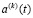дает решение дифференциального уравнения второго порядка (11), которое целесообразно для наглядности записать в виде

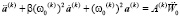. (12)

Здесь:

– собственная частота

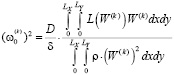; (13)

– масштабный коэффициент

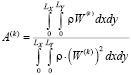(14)

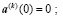
Для получения однозначного решения уравнения (12) необходимы начальные условия, которые в соответствии с выражениями (8) принимают вид 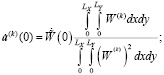(15)

(15)

Нахождение функций времени 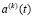позволяет, используя выражение для прогиба 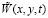, получить решение в виде пространственно-временного процесса колебаний при выбранном временном масштабе.

Для заданного воздействия 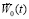на области крепления узла на печатной плате можно аппроксимировать функцию 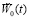значениями отсчетов через интервалы времени 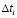[4, 5]. При аппроксимации функции с требуемой точностью e уравнение (12) для интервала 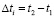будет иметь вид:

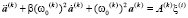. (16)

Здесь

.

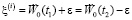В общем виде для каждого интервала 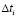решение уравнения (16) может иметь вид

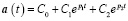при 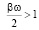; (17)

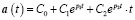при 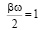; (18)

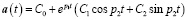при 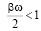. (19)

Здесь .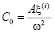

Для процесса затухающих колебаний при βw/2<1:

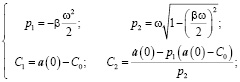(20)

При переходе к следующему интервалу необходимо изменение начальных условий и формирование нового временного интервала для решения задачи определения функции прогиба 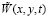. Уравнения (17) (18) (19) соответствуют затухающему процессу колебаний.

Решение задачи осуществляется на основе метода конечных разностей. Алгоритм моделирования колебаний сводится к формированию конечно-разностного аналога уравнения (4), решению с учетом граничных условий, обусловленных способом закрепления, видом функции плотности 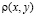в соответствии в соответствии с массой навесных элементов и массой материала платы печатного узла.

Задается начальное приближение собственной формы колебаний 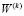, например, 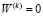для закрепленных областей и 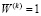в свободной от закрепления области. Вычисляется частотный параметр :

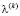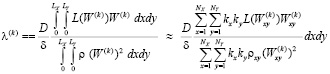. (21)

Здесь kx, ky – интегральные коэффициенты; Nx, Ny – количество узлов сеточной модели по направлениям осей координат.

Уточняется значения дискретного представления собственной формы 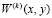, в соответствии со свободными узлами сеточной модели и значение частотного параметра 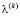. На заключительном этапе выполняется развертка во времени функций, характеризующих реакцию печатного узла на заданные воздействия.

Результаты определения собственных форм и частоты для пластины прямоугольной формы закрепленной в центре с однородным распределением массы показаны на рис. 1 [6]. Форма колебаний соответствует прогибу на 1-й, 6-й, 10-й и 13-й собственных частотах.

а б

в г

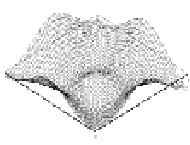
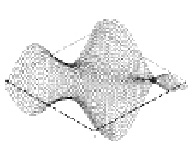
Рис. 1. Собственные формы колебаний закрепленной в центре прямоугольной пластины: первая (а), шестая (б), десятая (в), тринадцатая (г)

а б

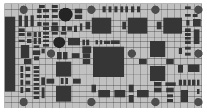
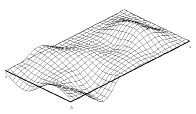
Рис. 2. а – графическое представление модели узла на печатной плате в программном комплексе моделирования динамики пластинчатых конструкций; б – прогиб узла на печатной плате при ударном воздействии

На рис. 2 показана модель узла на печатной плате и график прогиба при ударном воздействии. Узел имеет одиннадцать точек крепления. Показан прогиб платы с учетом первых семи форм колебаний в диапазоне частот от 100 до 2000 Гц.

При моделировании динамики узлов на печатных платах электронной аппаратуры необходимо исследовать колебания в широком частотном диапазоне. Это позволит выявить в конструкции локальные области механических напряжений и наиболее интенсивных виброперегрузок при эксплуатационных воздействиях.

Обоснованные конструктивные решения по повышению устойчивости изделий к механическим воздействиям могут быть приняты по результатам оценки динамических характеристик на этапе проектирования узлов электронной аппаратуры и приборов.

Библиографическая ссылка