Отметим сразу, что изучение действительных чисел в вузе должно достаточно сильно отличаться от изучения этой темы в школе [12]. Тема «Действительные числа» излагается» различными лекторами и авторами учебников по разному. Традиционно используются аксиоматический метод [2-5] и метод бесконечных десятичных дробей [9-11, 16-19]. Есть еще метод сечений Дедекинда [7, 8, 13]. Связь между указанными методами слабая, и настоящий обзор вместе с [14, 15] частично восполняет данный пробел.
Действительно, если множество не строится конкретно, а задается условиями, то нельзя быть уверенным в его существовании. Это показывает, например, парадокс Рассела [6], который приводится в первом пункте настоящего обзора.
В [9-11, 16-19] действительные числа определяются при помощи бесконечных десятичных дробей. Однако для обоснования свойств действительных чисел привлекаются понятия точных верхней и нижней граней [9, 10, 16] и предела последовательности [17-19]. С другой стороны, понятия точных верхней и нижней граней требуют определения действительного числа, обоснования свойств упорядоченности действительных чисел, а традиционное определение предела последовательности [2-5, 11] требует еще и обоснования арифметики действительных чисел.
Для определения точной верхней грани [16, 18, 19] должно быть определено действительное число и должны быть определены отношения порядка: больше, меньше, равно. В [16] определения точных верхней и нижней граней используются для обоснования арифметики действительных чисел.
В [17-19] вводится предел последовательности, который требует лишь определения и упорядоченности действительных чисел и для обоснования арифметики действительных чисел, чем обеспечивается меньшая, чем в [16], трудоемкость этого обоснования.
Итак, в [2-5] арифметика действительного числа содержится в его определении, а понятия точных граней и предела последовательности даются потом, в [17-19] одно из этих понятий обязательно привлекается для обоснования арифметики действительных чисел. В [15] показано, что, определив действительные числа бесконечными десятичными дробями, можно доказать аксиомы действительных чисел в качестве свойств, не привлекая понятия точных граней и предела последовательности.
В настоящем обзоре мы дадим аналогичный [15] подход изложения этой темы, но с некоторыми изменениями, связанными с удобством и компактностью.
1. Понятие множества, основные обозначения, парадокс Рассела
Множество в математике – понятие исходное, оно не определяется и означает набор или совокупность. Множество состоит из объектов, которые называются его элементами. Множества обычно обозначают большими буквами, а элементы множеств – малыми.
Основные обозначения:
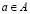 – элемент a принадлежит множеству A,
– элемент a принадлежит множеству A, 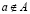 – элемент a не принадлежит множеству A,
– элемент a не принадлежит множеству A, 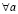 – для любого a,
– для любого a, 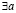 – существует a, a: – a, такой что,
– существует a, a: – a, такой что, 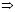 – следует,
– следует, 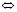 – равносильно.
– равносильно.
Запись 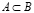 означает, что множество A является подмножеством множества B, т.е.
означает, что множество A является подмножеством множества B, т.е. 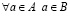 . Если
. Если 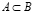 и
и 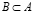 , то пишут
, то пишут 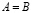 . Запись
. Запись 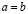 означает, что a и b – это один и тот же элемент, причем должны быть справедливы свойства рефлексивности:
означает, что a и b – это один и тот же элемент, причем должны быть справедливы свойства рефлексивности: 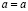 ; взаимности:
; взаимности: 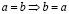 ; транзитивности:
; транзитивности: 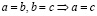 .
.
Объединением множеств A и B, т.е. 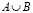 назовем множество, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из множеств A, B.
назовем множество, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из множеств A, B.
Пересечением множеств A и B, т.е. 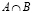 , назовем множество, состоящее из всех элементов, каждый из которых принадлежит как множеству A, так и множеству B.
, назовем множество, состоящее из всех элементов, каждый из которых принадлежит как множеству A, так и множеству B.
Разностью множеств A и B, т. е. 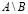 , назовем множество, состоящее из всех элементов A, не входящих во множество B.
, назовем множество, состоящее из всех элементов A, не входящих во множество B.
Вводится пустое множество ∅ – множество, не содержащее ни одного элемента.
Примеры множеств: 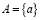 – множество из одного элемента,
– множество из одного элемента, 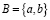 – множество из двух элементов, если эти элементы различны. Однако какое-нибудь множество может содержаться в другом множестве в качестве элемента, например:
– множество из двух элементов, если эти элементы различны. Однако какое-нибудь множество может содержаться в другом множестве в качестве элемента, например:
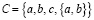 ;
;
здесь также предполагается, что a,b и c– различны.
Понятие множества противоречиво. Это показывают парадоксы Бертрана Рассела, один из которых мы приведем [17].
Парадокс Рассела. Множество должно быть определено так, чтобы для любого объекта существовал однозначный ответ на вопрос, принадлежит ли выбранный объект рассматриваемому множеству.
Пусть множество F содержит все те и только те множества, которые не являются элементами самих себя (не содержат себя в качестве элемента):
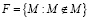 .
.
Парадокс состоит в том, что после такого способа задания множества F невозможно однозначно ответить на вопрос: само множество F как элемент принадлежит F или нет.
В самом деле, если предположить, что 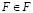 , то тогда F является элементом самого себя и не может, согласно определению, принадлежать F, т.е.
, то тогда F является элементом самого себя и не может, согласно определению, принадлежать F, т.е. 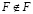 .
.
Если же предположить, что 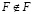 , то это означает, что F не является элементом самого себя и, поэтому, F как элемент должен принадлежать F, т. е. <<cher26.wmf>>.
, то это означает, что F не является элементом самого себя и, поэтому, F как элемент должен принадлежать F, т. е. <<cher26.wmf>>.
2. Аксиоматический метод введения действительных чисел
Непустое множество R называется множеством действительных (вещественных) чисел, а его элементы – действительными (вещественными) числами, если на R определены операции сложения и умножения и отношение порядка, удовлетворяющие следующим свойствам [2].
I. Свойства сложения:
1. 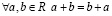 (коммутативность);
(коммутативность);
2. 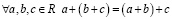 (ассоциативность);
(ассоциативность);
3. 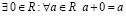 ;
;
4. 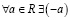 – число противоположное
– число противоположное 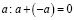 .
.
Число 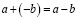 – называется разностью a и b.
– называется разностью a и b. 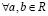 .
.
II. Свойства умножения:
1. 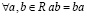 (коммутативность);
(коммутативность);
2. 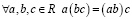 (ассоциативность);
(ассоциативность);
3. 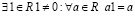 ;
;
4. 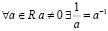 – число обратное
– число обратное 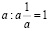 .
.
Число 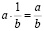 – называется частным от деления a на b.
– называется частным от деления a на b. 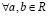 и
и 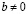 .
.
III. Свойство сложения и умножения:
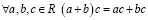 (дистрибутивность умножения относительно сложения).
(дистрибутивность умножения относительно сложения).
IV. Упорядоченность и ее связь со сложением и умножением. Для любых различных a и b из R справедливо отношение 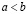 , или, что то же самое,
, или, что то же самое, 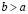 , либо
, либо 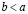 , или, что то же самое,
, или, что то же самое, 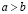 . При этом должны быть выполнены свойства:
. При этом должны быть выполнены свойства:
1. если 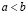 и
и 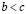 , то
, то 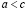 (транзитивность);
(транзитивность);
2. если 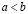 , то
, то 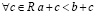 ;
;
3. если 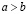 и
и 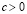 то
то 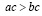 .
.
Множества, удовлетворяющие IV и IV 1 называются упорядоченными.
V. Непрерывность. Пусть X и Y – непустые множества R, такие что
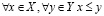 .
.
Тогда 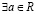 , такое что
, такое что
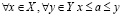 . (2.1)
. (2.1)
Замечание 1. Множество Q рациональных чисел удовлетворяет всем аксиомам, кроме V.
Действительно, пусть
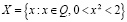 ,
,
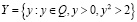 .
.
Тогда в Q не существует a со свойством (2.1).
Следствия из аксиом I – V.
1. Число 0 единственно.
Действительно, пусть существуют 0 и 0', удовлетворяющие I 3. Тогда, в силу I 1 и I 3
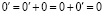 .
.
2. Число (–a) единственно.
Действительно, пусть существуют (–a) и 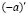 , удовлетворяющие I 4. Тогда, в силу I 1, I 2 и I 3
, удовлетворяющие I 4. Тогда, в силу I 1, I 2 и I 3
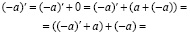
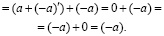
3. Аналогично 1 и 2 обосновывается единственность 1 и 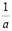 при
при 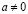 .
.
4. 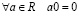 .
.
Это следует из того, что в силу II 3, II 1, III справедливы равенства, означающие, что 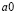 удовлетворяет I 3:
удовлетворяет I 3:
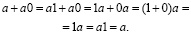
5. 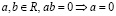 , или
, или 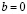 .
.
От противного, пусть 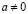 и
и 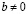 , тогда, умножив
, тогда, умножив 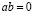 на
на 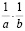 и используя II 1, II 2 и II 4, получим
и используя II 1, II 2 и II 4, получим 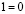 , что противоречит II 3.
, что противоречит II 3.
6. 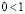 .
.
От противного, пусть 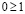 , тогда из II 3 следует, что
, тогда из II 3 следует, что 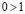 , или, что то же самое,
, или, что то же самое, 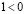 . Согласно I 4 существует
. Согласно I 4 существует 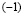 . Пользуясь IV 2, из последнего неравенства получаем
. Пользуясь IV 2, из последнего неравенства получаем 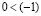 , или, что то же самое,
, или, что то же самое, 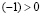 . Обратимся к IV 3 при
. Обратимся к IV 3 при 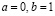 и
и 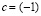 . Это возможно в силу того, что
. Это возможно в силу того, что 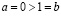 и, поскольку, мы только что доказали, что
и, поскольку, мы только что доказали, что 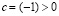 . В результате получаем
. В результате получаем 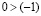 , что противоречит неравенству
, что противоречит неравенству 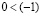 , полученному ранее.
, полученному ранее.
Замечание 2. Ввиду парадокса Рассела возникает вопрос: не получим ли мы во множестве R противоречивого следствия, как это произошло с множеством F предыдущего пункта. Для этого мы построим множество R с помощью бесконечных десятичных дробей.
3. Определение действительных чисел, их упорядоченность и непрерывность
В процессе счета возникают натуральные числа 1, 2, 3, …, n, …, . Множество натуральных чисел обозначим N, а множество целых – Z. Потребности практики приводят к необходимости введения рациональных чисел, т.е. чисел вида 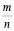 , где m – целое, а n – натуральное число. Множество рациональных чисел обозначим Q. Однако, как показывает теория измерений, этого недостаточно, возникает потребность дальнейшего расширения понятия числа.
, где m – целое, а n – натуральное число. Множество рациональных чисел обозначим Q. Однако, как показывает теория измерений, этого недостаточно, возникает потребность дальнейшего расширения понятия числа.
Всюду в дальнейшем предполагаются известными свойства рациональных чисел [18] (более точно, предполагаются известными свойства конечных десятичных дробей).
Бесконечными десятичными дробями называются символы вида 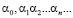 и
и 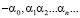 , где
, где 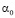 – любое целое неотрицательное число, а каждое
– любое целое неотрицательное число, а каждое 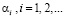 – одна из цифр
– одна из цифр 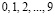 .
.
Определение 1. Действительным числом называется любая бесконечная десятичная дробь.
Если 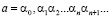 , то рациональное число
, то рациональное число 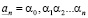 называется нижним n-значным приближением действительного числа, а число
называется нижним n-значным приближением действительного числа, а число 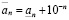 – верхним n-значным приближением.
– верхним n-значным приближением.
Если 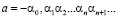 , то, соответственно,
, то, соответственно, 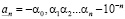 ,
, 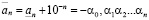 . Легко видеть, что
. Легко видеть, что
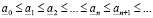 , (3.1)
, (3.1)
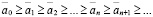 . (3.2)
. (3.2)
Множество действительных чисел обозначим R.
Определение 2. Если для двух действительных чисел a и b существует такое целое неотрицательное n0, что
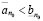 , (3.3)
, (3.3)
то 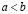 , или, что то же самое,
, или, что то же самое, 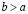 , если же существует такое целое неотрицательное
, если же существует такое целое неотрицательное 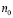 , такое что, то
, такое что, то
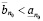 , (3.4)
, (3.4)
то 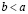 , или, что то же самое,
, или, что то же самое, 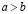 . Если же не выполняется ни первое условие ни второе, то
. Если же не выполняется ни первое условие ни второе, то 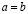 .
.
Следствие. Если выполнено (3.3), то
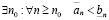 , (3.5)
, (3.5)
аналогично, если выполнено (3.4), то
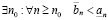 . (3.6)
. (3.6)
Действительно, обращаясь к (3.3) и (3.1), (3.2), получаем
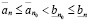 ,
,
откуда и следует (3.5). Аналогично, из (3.4), (3.1) и (3.2) будем иметь
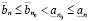 ,
,
откуда и следует (3.6).
Лемма о транзитивности. Если 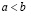 и
и 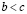 , то
, то 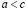 .
.
Действительно, т.к. 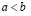 , то
, то
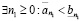 ,
,
а если 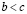 , то
, то
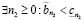 .
.
Положим 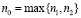 . Тогда, на основании (3.5) и (3.6)
. Тогда, на основании (3.5) и (3.6)
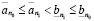 ,
, 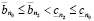 ,
,
откуда
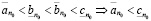 .
.
Из последнего равенства следует, что 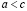 .
.
Если для некоторых действительных a и bсправедливо либо строгое неравенство 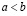 , либо равенство
, либо равенство 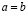 , то, объединяя их, пишут нестрогое неравенство
, то, объединяя их, пишут нестрогое неравенство 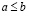 , или, что то же самое,
, или, что то же самое, 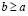 .
.
Критерий равенства. Для справедливости равенства 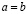 необходима и достаточна справедливость неравенства
необходима и достаточна справедливость неравенства
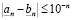 , (3.7)
, (3.7)
для любого целого неотрицательного n.
Доказательство. Пусть 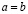 . На основании определения 2 для любого целого неотрицательного n справедливы неравенства
. На основании определения 2 для любого целого неотрицательного n справедливы неравенства
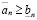 (3.3')
(3.3')
и
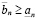 . (3.4')
. (3.4')
Из (3.3') имеем
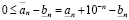 ,
,
т.е.
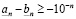 . (3.8)
. (3.8)
Из (3.4') получим
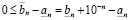 ,
,
значит
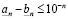 . (3.9)
. (3.9)
Из (3.8) и (3.9) следует (3.7).
Обратно, пусть справедливо (3.7), следовательно справедливы (3.8) и (3.9), из которых следуют (3.3') и (3.4') соответственно. Тогда, по определению 2, следует, что 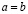 . Критерий доказан.
. Критерий доказан.
Если числа a и b имеют одно и то же представление бесконечной десятичной дробью, то они равны.
Действительно, если представление одно и то же, то для любого целого неотрицательного n 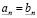 . Из критерия равенства, применяя (3.7), получаем искомое утверждение.
. Из критерия равенства, применяя (3.7), получаем искомое утверждение.
Числа вида
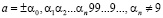 ,
,
и
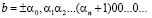 ,
,
также будут равными [14–15].
Принцип Архимеда. Для любого действительного числа a существует натуральное число, большее a.
Доказательство. Если 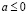 , то это натуральное число может быть равно 1. Если
, то это натуральное число может быть равно 1. Если 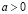 , то, т.к.
, то, т.к. 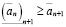
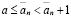 для любого целого неотрицательного n. Но, поскольку,
для любого целого неотрицательного n. Но, поскольку,
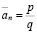 ,
,
где p и q – натуральны, то
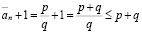 .
.
Поэтому, в качестве искомого натурального числа мы возьмем 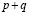 , где p и q – числитель и знаменатель
, где p и q – числитель и знаменатель 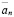 соответственно.
соответственно.
Принцип математической индукции. Пусть множество 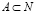 , N – множество натуральных чисел, которое обладает свойствами:
, N – множество натуральных чисел, которое обладает свойствами:
1˚. 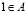 ;
;
2˚. 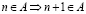 .
.
Тогда 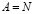 . [3, 4, 14].
. [3, 4, 14].
Этот принцип берется в качестве аксиомы натуральных чисел [3, 4, 14].
Плотность рациональных чисел во множестве действительных. Для любых действительных чисел a и b таких, что 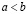 , существует рациональное число r, удовлетворяющее неравенству
, существует рациональное число r, удовлетворяющее неравенству 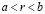 .
.
Доказательство. Если 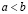 , то согласно следствию из определения 2, существует натуральное n0, такое что для любого натурального
, то согласно следствию из определения 2, существует натуральное n0, такое что для любого натурального 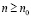 справедливо неравенство
справедливо неравенство
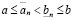 .
.
Положив 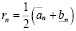 , поскольку
, поскольку 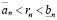 , получаем справедливость неравенства
, получаем справедливость неравенства 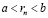 . Таким образом, в качестве r в требуемом неравенстве можно взять любое rn при
. Таким образом, в качестве r в требуемом неравенстве можно взять любое rn при 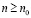 .
.
Замечание. Рациональных чисел r между a и b можно вставить бесконечно много.
Действительно, рациональных чисел между a и b можно вставить бесконечно много, поскольку в качестве рационального r между a и b можно взять любое rn при натуральных 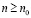 , а их бесконечно много.
, а их бесконечно много.
Лемма о равенстве. Если две разные десятичные дроби равны, то одна из них конечная, а другая периодическая с периодом 9.
Доказательство. Пусть даны две разные десятичные дроби:
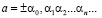 ,
,
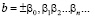 и
и 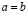 .
.
Пусть l – наименьшее число, для которого 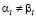 . По критерию равенства
. По критерию равенства 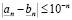 . Далее,
. Далее,
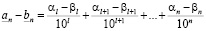 .
.
В силу оценки
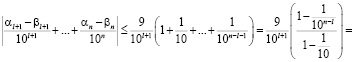
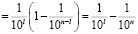 ,
,
имеем
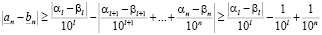 .
.
Таким образом,
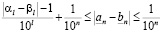 ,
,
откуда
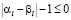 . (3.10)
. (3.10)
Пусть, для определенности 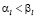 , тогда из (3.10) следует, что
, тогда из (3.10) следует, что
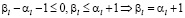 ,
,
и тогда
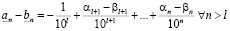 . (3.11)
. (3.11)
Положим в (3.11) 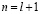 , отсюда
, отсюда
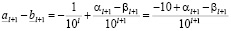 .
.
Из критерия равенства получаем 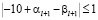 . Поскольку
. Поскольку
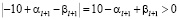 ,
,
то либо
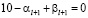 ,
,
либо
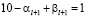 .
.
Если
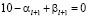 ,
,
то 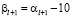 , что невозможно, поскольку
, что невозможно, поскольку 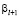 – цифра от 0 до 9. Если
– цифра от 0 до 9. Если
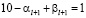 ,
,
то 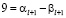 , а поскольку
, а поскольку 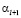 такая же цифра от 0 до 9, то
такая же цифра от 0 до 9, то 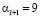 , а
, а 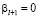 и, кроме того:
и, кроме того:
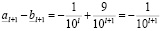 ,
,
и из (3.11)
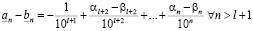 . (3.11')
. (3.11')
Повторяя те же рассуждения, получим 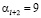 ,
, 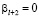 и т.д.
и т.д.
Из определения 2 следуют свойства равенств: рефлексивности и взаимности, а из леммы о равенстве следует свойство транзитивности [9, 10].
Итак, во множестве чисел введены отношения порядка: «меньше», «больше», «равно» и доказано, что для любых двух действительных чисел выполняется лишь одно из этих трех отношений порядка. Причем для этих отношений порядка выполнены условия транзитивности. Такие множества называются упорядоченными [10, 11].
Следствие из леммы о транзитивности. Если 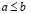 и
и 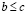 , то
, то 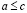 .
.
Доказательство следует из леммы о транзитивности и транзитивности равенства.
В дальнейшем, где это возможно, будем исключать из рассмотрения периодические десятичные дроби с периодом 9 [10, 11].
Достаточное условие равенства. Пусть для двух действительных чисел a и b и любого целого неотрицательного n существуют рациональные числа rn и Rn и целое неотрицательное N, удовлетворяющие неравенствам
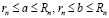 ; (3.12)
; (3.12)
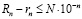 . (3.13)
. (3.13)
Тогда, 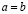 .
.
Доказательство. Предположим противное: 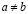 . Пусть для определенности
. Пусть для определенности 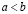 . Тогда, на основании (3.1), (3.2), (3.3) и (3.12) имеем
. Тогда, на основании (3.1), (3.2), (3.3) и (3.12) имеем
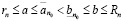 . (3.14)
. (3.14)
По лемме о транзитивности неравенство (3.14) упрощается до неравенства, содержащего лишь рациональные числа:
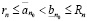 . (3.15)
. (3.15)
Из (3.15) [17] мы получим
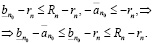
Из неравенства (3.13) и последнего следует, что
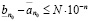 ,
,
или
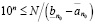 .
.
Последнее должно быть справедливо для любого целого неотрицательного n. Поскольку 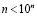 , то для любого целого неотрицательного n справедливо неравенство
, то для любого целого неотрицательного n справедливо неравенство
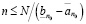 ,
,
а это противоречит принципу Архимеда.
Теорема непрерывности. Пусть X и Y– непустые множества из R, такие что
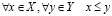 . (3.16)
. (3.16)
Тогда
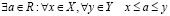 . (3.17)
. (3.17)
Доказательство. В силу (3.16) зафиксируем 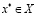 и
и 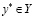 . Если
. Если 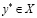 , то
, то 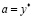 и (3.17) доказано. Пусть, далее
и (3.17) доказано. Пусть, далее 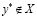 . Отметим, что определить действительное число означает указать правило, по которому с помощью конечного числа операций можно найти n-значное приближение
. Отметим, что определить действительное число означает указать правило, по которому с помощью конечного числа операций можно найти n-значное приближение 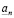 числа a для любого целого неотрицательного n, и при этом должно быть выполнено неравенство
числа a для любого целого неотрицательного n, и при этом должно быть выполнено неравенство
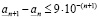 , (3.18)
, (3.18)
т.к. это неравенство вытекает из определения бесконечной десятичной дроби [6, 7, 8, 9, 10, 11]. Построим число a, указав способ вычисления его n – значного приближения 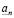 . Рассмотрим множество рациональных чисел
. Рассмотрим множество рациональных чисел 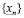 , каждое из которых является n-значным приближением
, каждое из которых является n-значным приближением 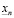 всех чисел
всех чисел 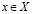 между
между 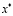 и
и 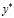 . Хотя X может быть бесконечным, тем не менее, множество
. Хотя X может быть бесконечным, тем не менее, множество 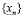 n-значных приближений – конечно. В самом деле, между
n-значных приближений – конечно. В самом деле, между 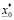 и
и 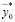 содержится конечное число рациональных чисел, имеющих n знаков после запятой. Количество таких дробей ограничено сверху числом
содержится конечное число рациональных чисел, имеющих n знаков после запятой. Количество таких дробей ограничено сверху числом 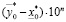 . В конечном множестве
. В конечном множестве 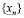 есть наибольший элемент, его мы и выберем в качестве n-значного приближения
есть наибольший элемент, его мы и выберем в качестве n-значного приближения 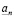 :
:
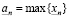 . (3.19)
. (3.19)
Построенные приближения удовлетворяют неравенству (3.18), т.к. нарушение этого неравенства означало бы, что 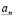 не есть наибольший элемент множества
не есть наибольший элемент множества 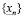 . Действительно, пусть
. Действительно, пусть
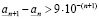 . (3.20)
. (3.20)
Существует 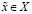 , такое что
, такое что
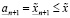 , (3.21)
, (3.21)
т.е. в X должно существовать число 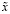 , такое что его (n+1)-значное приближение с недостатком совпадает с
, такое что его (n+1)-значное приближение с недостатком совпадает с 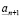 . Но тогда
. Но тогда
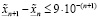 , (3.18′)
, (3.18′)
потому что 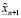 и
и 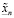 – суть
– суть 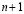 и n-значные приближения
и n-значные приближения 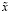 . Отсюда, получаем
. Отсюда, получаем
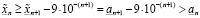 ,
,
а значит
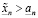 . (3.22)
. (3.22)
Здесь мы выразили 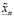 из (3.18′), воспользовались (3.21), а, затем, и (3.20). Неравенство (3.22) противоречит (3.19).
из (3.18′), воспользовались (3.21), а, затем, и (3.20). Неравенство (3.22) противоречит (3.19).
Итак, число a определено.
Докажем теперь, что построенное число a удовлетворяет (3.17).
Сначала, докажем, что
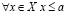
от противного. Пусть существует число 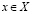 , такое что
, такое что 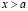 . Поэтому, что существует целое неотрицательное m, такое что
. Поэтому, что существует целое неотрицательное m, такое что 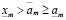 . Но последнее невозможно в силу (3.19).
. Но последнее невозможно в силу (3.19).
Теперь докажем, что
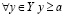
от противного. Пусть существует число 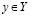 , такое что
, такое что 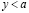 . Это значит, что существует целое неотрицательное p, такое что
. Это значит, что существует целое неотрицательное p, такое что 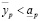 . Но тогда, существует
. Но тогда, существует 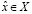 , такое что
, такое что 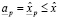 . С другой стороны,
. С другой стороны, 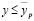 . Т.о.,
. Т.о.,
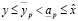 ,
,
или 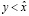 , что противоречит (3.16). Последнее завершает доказательство (3.17).
, что противоречит (3.16). Последнее завершает доказательство (3.17).
Лемма о числе. Для любого действительного числа a и любых целых неотрицательных m и n справедливо неравенство
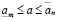 . (3.23)
. (3.23)
Доказательство. Существование a в (3.23) следует из теоремы непрерывности. Действительно, пусть множество 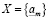 , а множество
, а множество 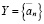 . Нужно доказать лишь справедливость (3.16), т.е.
. Нужно доказать лишь справедливость (3.16), т.е.
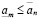 , (3.16′)
, (3.16′)
для любых целых неотрицательных m и n. Но из (3.1) и (3.2) можно заключить, что
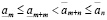 , (3.16″)
, (3.16″)
откуда следует неравенство более сильное, чем (3.16′):
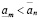 . (3.16′″)
. (3.16′″)
Единственность a из (3.23) докажем от противного. Пусть существуют a и b не обязательно равные между собой, удовлетворяющие (3.23). Поскольку b удовлетворяет (3.23), то
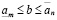 . (3.23')
. (3.23')
Положив, теперь, в (3.23) и (3.23') 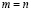 , получим
, получим
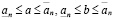 . (3.23″)
. (3.23″)
Поскольку,
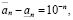
то на основании (3.23″), последнего равенства и достаточного условия равенства заключаем, что 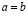 .
.
Лемма Дедекинда. Пусть множества X и Y, состоящие из рациональных чисел таковы, что:
а) любое рациональное число попадает либо в X, либо в Y;
б) множества X и Y непустые;
в) 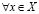 и
и 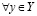
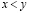 . (3.24)
. (3.24)
Тогда, существует единственное действительное число a такое, что
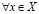 и
и 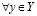
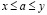 . (3.25)
. (3.25)
Доказательство. Из неравенства (3.24) следует справедливость (3.16), поэтому выполнено (3.17). Следовательно, существование a из (3.25) прямо следует из теоремы непрерывности.
Докажем единственность a из (3.25). Рассуждаем от противного, т.е. пусть существует 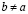 , удовлетворяющее (3.25), а именно:
, удовлетворяющее (3.25), а именно:
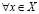 и
и 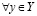
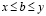 . (3.25')
. (3.25')
Пусть для определенности 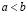 . Согласно плотности рациональных чисел во множестве действительных, существует рациональное r, удовлетворяющее неравенству
. Согласно плотности рациональных чисел во множестве действительных, существует рациональное r, удовлетворяющее неравенству 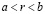 , и тогда
, и тогда 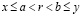 для любого
для любого 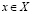 и любого
и любого 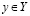 . Поскольку
. Поскольку 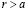 , то в силу (2.25) r не может принадлежать X. Поскольку
, то в силу (2.25) r не может принадлежать X. Поскольку 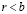 , то в силу (2.25′) r не может принадлежать Y. Т.о.,
, то в силу (2.25′) r не может принадлежать Y. Т.о., 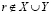 , что противоречит условию и лемма доказана.
, что противоречит условию и лемма доказана.
Теорема Дедекинда. Пусть множества X и Y, состоящие из действительных чисел таковы, что:
а) любое действительное число попадает либо в X, либо в Y;
б) множества X и Y непустые;
в) 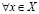 и
и 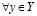
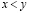 . (3.26)
. (3.26)
Тогда, существует единственное действительное число a такое, что
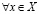 и
и 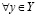
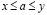 . (3.27)
. (3.27)
Доказательство. Из неравенства (3.26) следует справедливость (3.16), поэтому выполнено (3.17). Следовательно, существование a из (3.27) прямо следует из теоремы непрерывности.
Докажем единственность a из (3.27). Рассуждаем от противного, т.е. пусть существует 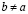 , удовлетворяющее (3.27), а именно:
, удовлетворяющее (3.27), а именно:
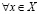 и
и 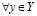
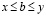 . (3.27')
. (3.27')
Пусть для определенности 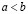 . Согласно плотности рациональных чисел во множестве действительных, существует рациональное r, удовлетворяющее неравенству
. Согласно плотности рациональных чисел во множестве действительных, существует рациональное r, удовлетворяющее неравенству 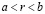 , и тогда
, и тогда 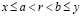 для любого
для любого 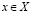 и любого
и любого 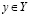 . Поскольку
. Поскольку 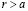 , то в силу (3.27) r не может принадлежать X. Поскольку
, то в силу (3.27) r не может принадлежать X. Поскольку 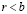 , то в силу (2.27′) r не может принадлежать Y. Таким образом,
, то в силу (2.27′) r не может принадлежать Y. Таким образом, 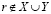 , что противоречит условию и теорема доказана.
, что противоречит условию и теорема доказана.
Замечание. Лемма Дедекинда, которой нет в [16], на наш взгляд, очень важна, т.к. она фактически устанавливает связь между подходами к определению действительного числа при помощи бесконечных десятичных дробей и определением действительного числа через сечения множества рациональных чисел по Дедекинду [14, 15].
4. Геометрическая интепретация действительных чисел
Геометрически множество действительных чисел изображается направленной (ориентированной) прямой, а отдельные числа – точками этой прямой. Поэтому, совокупность действительных чисел часто называют числовой прямой, а также числовой или действительной осью, а отдельные числа – ее точками. При такой интерпретации действительных чисел иногда вместо a меньше b (b больше a) говорят, что точка a лежит левее точки b (b лежит правее a).
Пусть a и b – действительные числа и 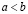 . Тогда интервал и отрезок определяются равенствами
. Тогда интервал и отрезок определяются равенствами 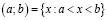 и
и 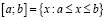 соответственно. В свою очередь, полуинтервалы аналогично определяются равенствами
соответственно. В свою очередь, полуинтервалы аналогично определяются равенствами
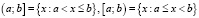 .
.
Интервал, отрезок и полуинтервалы называются конечными промежутками. Часто термин «конечные» опускается. Длину этих промежутков будем считать 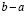 .
.
Бесконечные промежутки определяются равенствами:
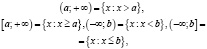
и 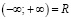 .
.
Замечание. Отметим, что в теореме Дедекинда в качестве множества действительных чисел, которое состоит из X и Y, не обязательно брать всю действительную прямую. В качестве этого множества можно взять любой промежуток действительной прямой, например 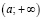 .
.
Библиографическая ссылка
Черняев А.П. МЕТОДИЧЕСКИЕ АСПЕКТЫ В ПРЕПОДАВАНИИ ТЕМЫ «ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА» В ВУЗАХ С УСИЛЕННОЙ МАТЕМАТИЧЕСКОЙ ПРОГРАММОЙ // Научное обозрение. Педагогические науки. 2016. № 3. С. 130-138;URL: https://science-pedagogy.ru/ru/article/view?id=1502 (дата обращения: 05.01.2026).


 science-review.ru
science-review.ru