science-review.ru
Уровень знаний, формирование умений и навыков, а также профессиональная готовность выпускников вуза, отставая от темпов развития мирового научно-технического прогресса, стали не соответствовать новым условиям и требованиям жизни. В связи с выдвинутыми условиями и требованиями общество нуждается в специалистах, которые были бы близки к примерно составленной обществом идеальной модели специалиста. Такая потребность привела к необходимости реформы и в системе образования Кыргызской Республики. В связи с чем и были разработаны новые Государственные образовательные стандарты.
В Государственном образовательном стандарте высшего профессионального образования Кыргызской Республики определены цели направления «550200 – Физико-математическое образование» в области обучения – подготовка педагога, способного решать профессиональные задачи непрерывного компетентностно-ориентированного образования в условиях быстро меняющегося мира; в области воспитания личности – развитие социально-личностных качеств студентов: целеустремленности, организованности, ответственности, гражданственности, коммуникативности, толерантности и т.д., повышение их общей культуры, стремления к самореализации и самосовершенствованию в профессии в рамках непрерывного образования и самообразования [1].
В последнее время будущая успешная профессиональная деятельность студента стала зависеть не только от его предметного знания, но и от способностей к творческому саморазвитию, самореализации, самообразованию и самовоспитанию, короче говоря, от «самости» студента, а также от уровня мышления.
В.И. Андреев определяет творческое саморазвитие личности как «особый вид творческой деятельности субъект-субъектной ориентации, направленной на интенсификацию и повышение эффективности процессов самости, среди которых системообразующими являются самоопределение, самоуправление, творческая самореализация и самосовершенствование личности» [2]. Отсюда следует, что в настоящее время саморазвитие студента является одной из приоритетных задач высшего образования. Для формирования «самости» студента самостоятельная форма работ является важной составляющей педагогического процесса и основным рычагом повышения качества образования. Поэтому в Государственном образовательном стандарте высшего профессионального образования выросла доля самостоятельной работы студента, являющаяся обязательным видом образовательной деятельности. В соответствии с этим коренным образом меняются формы и методы организации самостоятельной деятельности студентов.
Как известно, самостоятельная образовательная деятельность студентов предназначена не только для получения новых знаний, не приобретённых в аудитории по определенной дисциплине или при закреплении имеющихся знаний и умений, но и для формирования навыков самостоятельной работы в учебной, научной и профессиональной деятельностях, а также социально-личностных и профессиональных компетенций, мышлений, в том числе пространственного.
Таким образом, самостоятельная работа – форма организации образовательного процесса, стимулирующая активность, самостоятельность, познавательный интерес студентов [3].
В современном обществе, науке и технологии невозможно найти сферу деятельности человека, в которой бы не требовалось пространственного мышления.
Пространственное мышление – специфический вид мыслительной деятельности, которая необходима при решении задач, требующих ориентации в пространстве (как видимом, так и воображаемом), и основывается на анализе пространственных свойств и отношений реальных объектов или их графических изображений [4].
Пространственное мышление формируется и проявляется при создании определенных педагогических условий, одним из которых является самостоятельная работа студентов, используемая для решения задач, требующих создания геометрических образов и оперирования ими.
При профессиональной подготовке учителей математики по направлениям: психолого-педагогическое, методическое и предметное, не сформировав на должном уровне их пространственного мышления, нельзя ожидать высокого уровня пространственного мышления и у школьников. Всем известно, как высока роль геометрических задач при формировании упомянутого вида мышления. На этом этапе главной задачей для преподавателя является определение метода организации самостоятельной деятельности студента при решении таких задач. В настоящее время задания, составленные только на уровне знания и понимания, стали не актуальными. Если при традиционной технологии обучения на самостоятельную работу в основном выносились оставшиеся задачи номера, выполненного в аудитории, или же индивидуальные задания на вычисления, доказательства, построения, составления макетов и т.п., то теперь составляются задания с учетом применения новых технологий обучения, которые способствуют формированию профессиональных компетенций, а также направлены на формирование универсальных и социально-личностных компетенций и развитие мышлений (логического, пространственного, критического и т.д.), что отвечает требованиям общества. В зависимости от этого разрабатываются новые методы организации самостоятельной работы студентов.
Самостоятельная деятельность студента является одним из принципов «обучения в сотрудничестве», главной идеей которого является, как говорит Е.С. Полат, «учить и учиться вместе, а не просто выполнять вместе». Здесь происходит взаимодействие субъектами (студентами), а не студент-предмет.
Обучение в сотрудничестве (Cooperative Learning) – одна из технологий личностно ориентированного обучения, в котором есть малые группы обучающихся, объединенных общей целью, а именно оказать друг другу максимальную помощь в решении поставленных задач.
Групповая работа усиливает фактор мотивации и взаимной интеллектуальной активности, повышает эффективность познавательной деятельности студентов благодаря взаимному контролю [5]. При групповой самостоятельной работе происходит групповая самопроверка с последующей коррекцией преподавателя.
В работах [6–8] рассмотрены формы, методы и особенности организации самостоятельной работы студентов по дисциплине «Геометрия».
По проблеме развития пространственного мышления у будущих учителей математики в процессе изучения вузовских геометрических дисциплин занимаются В.А. Далингер, Е.А. Ермак, Р.Ф. Мамалыга, В.А. Василенко и др.
Однако организации самостоятельной работы при формировании пространственного мышления через геометрические задачи, в малых группах, посвящено немного работ.
Материалы и методы исследования
Предлагаем одну из методических разработок по организации самостоятельной деятельности студентов, на основе обучения в сотрудничестве при формировании пространственного мышления студентов в дисциплине «Геометрия».
Методическая разработка самостоятельной работы студента (решение задач с последующей мультимедийной презентацией)
I этап. Целеполагание
Раздел: «Плоскости и прямые в пространстве».
Цель: способствование развитию «самости» и формированию пространственного мышления студентов.
Задачи:
– закрепление и расширение аудиторных знаний, умений, полученных по разделу «Плоскости и прямые в пространстве»;
– формирование умения анализировать, решать и составлять задачи;
– формирование конструктивной способности;
– формирование навыков самоорганизации;
– формирование и развитие социальных качеств;
– формирование коммуникативных умений.
Вид деятельности: творческая.
Форма работы: групповая (5–6 человек).
Срок выполнения: среднесрочный (2 недели).
II этап. Составление заданий и разработка правил выполнения
Самостоятельная работа студентов по разделу «Плоскости и прямые в пространстве»
Этапы выполнения заданий
I этап.
1) Определить цели и задачи работы;
2) Составить план работы.
Задания (100 баллов).
II этап. Решение задач
1-вариант.
Решите задачи, полностью опишите решение, дайте соответствующее изображение
1. Найти ошибку в изображении (рисунок).
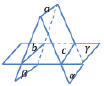
Даны взаимно пересекающиеся плоскости α,β и γ (5 баллов).
2. Даны прямые 
и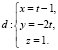 
а) найти геометрическое место точек середин отрезков данной длины δ, концы которых лежат на данных прямых (10 баллов);
б) найти фигуру, полученную при вращении прямой l вокруг d (10 баллов).
3. Даны точки M1 = (x1, y1, z1), M2 = (x2, y2, z2) и плоскость Ax + By + Cz + D = 0. Найти условия, необходимые и достаточные для того, чтобы данная плоскость пересекала а) прямую M1M2; б) отрезок M1M2 в его внутренней точке (20 баллов).
4. Составьте примеры и задачи, аналогичные предложенным (15 баллов).
III этап. Подготовка мультимедийной презентации по проделанной работе с помощью программы MS PowerPoint (30 баллов).
Литература. Указана в силлабусе.
IV этап. Защита выполненной работы. Устный доклад с мультимедийной презентацией (10 баллов)
Критерии оценивания
1. По результатам решенных задач.
1.1. Задача полностью решена правильно – 100 %.
1.2. При решении имеются незначительные недостатки – 90 %.
1.3. При решении имеются значительные недостатки – 70 %.
1.4. Задача решена частично: не рассмотрены все случаи – 50 %.
1.5. Задача решена частично: не рассмотрены все случаи, в рассмотренных случаях имеются недостатки – 30 %.
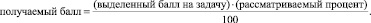
Например, если в третьей задаче не рассмотрен 2-й случай, то задача считается частично решенной, и при этом имеем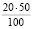 
= 10 баллов.
2. По подготовке мультимедийной презентации.
2.1. Презентация охватывает материал полностью, оформлена без замечаний – 30 баллов.
2.2. Презентация охватывает материал полностью, оформлена с 2–3 замечаниями – 25 баллов.
2.3. Презентация охватывает материал не полностью, оформлена с 2–3 замечаниями – 20 баллов.
2.4. Презентация охватывает материал не полностью, оформлена с 4 и более замечаниями – 15 баллов.
3. По изложению выполненной работы.
3.1. Доклад о выполненной работе сделан четко, понятно, без уточняющих вопросов – 10 баллов.
3.2. Доклад о выполненной работе сделан не очень четко и понятно, с уточняющими вопросами – 5–8 баллов.
Консультация (день недели ______, время____, место _____).
Защита работы 12–15 мин. Форма защиты произвольная (индивидуальная или групповая). Дата______
III этап. Оценивание
1. Групповое самооценивание работ малых групп по заданиям
|
1.1 |
1.2 |
1.3 |
1.4 |
2.1 |
2.2 |
2.3 |
2.4 |
3.1 |
3.2 |
Итого |
|
|
1 подгруппа |
|||||||||||
|
2 подгруппа |
|||||||||||
|
3 подгруппа |
|||||||||||
|
4 подгруппа |
|||||||||||
|
5 подгруппа |
2. Самооценивание в малых группах
|
Асанов А. |
Акматов Б. |
|||||
|
1 задача |
||||||
|
2 задача |
||||||
|
3 задача |
||||||
|
4 задача |
||||||
|
Подгот. презент. |
||||||
|
Доклад |
||||||
|
Итого |
3. Самооценивание студента
Что я смог сделать? ____________________________________
Что я не смог сделать? __________________________________
Что я не умею делать? __________________________________
Чему я должен научиться? _______________________________
Результаты исследования и их обсуждение
Здесь предложены задачи, по сложности соответствующие таксономии Блума, при этом ориентированы на «зону ближайшего развития» знаний студентов, а также на формирование их пространственного мышления. Так, например, при выполнении задачи 2б, несмотря на то что еще не пройдена тема «Поверхности второго порядка» и не ставилось условие определения взаимного расположения данных прямых, без которого невозможно найти ГМТ и фигуру вращения, студенты смогли определить вид поверхности (однополостный гиперболоид), полученной при вращении прямой l вокруг прямой d. В других вариантах было указано, что прямые либо пересекаются и перпендикулярны, либо параллельны, либо скрещиваются. В этих случаях соответственно ими были получены конус, цилиндр и внешняя область окружности, центр которой находится на прямой d, радиуса r, где r – расстояние между скрещивающимися прямыми. Все подгруппы с первым вопросом справились, смогли прочитать чертеж и нашли ошибку, опираясь на свойства взаимного расположения прямых и плоскостей, а также составили примеры и задачи, подобные данным.
На вопрос «Как была организована работа в малых группах?» студенты отвечали по-разному. Одна подгруппа сказала, что выбрали лидера, который распределил задания каждому, в другой подгруппе все решали задачи индивидуально, после чего все вместе обсудили полученные результаты, оформили решение, составили презентацию и провели групповую презентацию. Третья же подгруппа выбрала лидера, далее, разделившись по парам, участники распределили задания между собой, а затем сфокусировались и оформили сообща работу.
Выводы
Организация самостоятельной деятельности студента на уровне репродукции, от знания до понимания, не стала соответствовать внешним (общества) и внутренним (преподавателя и студента) требованиям к образовательному процессу. Всем хорошо известно, что одним из важнейших средств формирования пространственного мышления обучающихся и обучения их действиям по самостоятельному приобретению знаний являются математические задачи. При решении задач на уровне репродукции студенты используют только готовые формулы или свойства геометрических объектов, при этом для них важен правильный ответ. Все это указывает на то, что в этом случае у них на должном уровне не происходит формирования умений и навыков творческой деятельности, а также пространственного мышления, требующего создания пространственных образов и оперирования ими.
Если задания будут даны на продуктивном уровне, то при индивидуальном исследовании студент свою работу может считать качественно выполненной и завершенной, хотя такая самооценка может быть и ошибочной. При этом такие задания в случае групповой работы усиливают фактор взаимной интеллектуальной активности, благодаря взаимной помощи и контролю повышают эффективность познавательной деятельности, способствуют углублению и расширению знаний при взаимном обучении.
Результаты психологических исследований указывают на то, что студенты естественных факультетов отличаются некоммуникабельностью, застенчивостью, робостью, кроме того, на вышесказанную специальность в основном приходят выпускники сельских школ, с низким уровнем социабельности и интровертированностью. Однако будущая профессия требует от них не только знания предмета, но и способностей формирования социально-личностных компетенций учащихся, что должны быть сформировано у них за время обучения в вузе. Именно такая деятельность студентов и задания на продуктивном уровне усвоения знаний в сотрудническом взаимодействии являются основными педагогическими условиями при формировании как универсальных и профессиональных компетенций будущих специалистов, так и их пространственного мышления.
Библиографическая ссылка
Борбоева Г.М. ОРГАНИЗАЦИЯ САМОСТОЯТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ СТУДЕНТОВ В СОТРУДНИЧЕСТВЕ С ФОРМИРОВАНИЕМ ПРОСТРАНСТВЕННОГО МЫШЛЕНИЯ ПРИ ОБУЧЕНИИ ГЕОМЕТРИИ // Научное обозрение. Педагогические науки. – 2020. – № 1. – С. 59-63;URL: https://science-pedagogy.ru/ru/article/view?id=2275 (дата обращения: 23.11.2024).