Профессиональная деятельность значительной доли обучающихся и выпускников бакалавриата и магистратуры по направлениям «Химия» и «Химическая технология» связана с высокомолекулярными и элементоорганическими соединениями.
Согласно федеральным государственным образовательным стандартам, для студентов направлений подготовки бакалавриата и магистратуры «Химия» (04.03.01 и 04.04.01 соответственно) одними из объектов профессиональной деятельности являются молекулы и сложные соединения [1, 2]. Также выпускники бакалавриата должны уметь применять для решения профессиональных задач теоретические основы фундаментальных разделов химии (общепрофессиональная компетенция ОПК-1) и основные законы естественнонаучных дисциплин (ОПК-3), в том числе при анализе полученных результатов (профессиональная компетенция ПК-4) и при решении конкретных производственных задач (ПК-8) [1]. Магистры должны уметь применять основы как традиционных, так и новых областей химии (ОПК-1), владеть теорией в своей области химии (ПК-1) [2].
Для обучающихся на направлениях бакалавриата и магистратуры «Химическая технология» (18.03.01 и 18.04.01) объектами являются химические вещества [3, 4]. К компетенциям выпускников бакалавриата относят: использование естественнонаучных дисциплин в профессиональной деятельности (ОПК-1), использование знаний о строении вещества для понимания окружающего мира и явлений природы (ОПК-2), химических процессов в окружающем мире (ОПК-3) [3].
Для студентов профилей направлений «Химия» и «Химическая технология», которые связаны с высокомолекулярными и элементоорганическими соединениями, переработкой полимеров и эластомеров, технологиями волокон, лаков и красок, в перечисленные объекты и компетенции включают в том числе макромолекулы и комплексные соединения, которые используют в качестве катализаторов. При этом макромолекулы обладают рядом структурных особенностей относительно молекул низкомолекулярных соединений, связанных с длиной молекулы, их описывают рядом специфических моделей. Металлоорганические соединения, к примеру металлоценовые, также обладают необычной структурой, которую необходимо отдельно разъяснять при обучении.
О подходе к различным разделам химии, особенно структурной химии и химической динамики, с точки зрения начертательной геометрии писал А.А. Ищенко, он же обозначил необходимость преподавания начертательной геометрии и инженерной графики обучающимся на специальностях «Химия» и «Химическая технология» [5]. По причине наличия в учебных планах высших учебных заведений графических дисциплин, таких как начертательная геометрия, а также инженерная и компьютерная графика, которые значительно опираются на начертательно-геометрический базис, возможно связать их с химическими науками как дисциплины начальной и специальный профессиональной подготовки [6].
Подобный подход позволяет увеличить заинтересованность, более точно обозначить цель обучения и, как следствие, увеличить как уровень знаний по графическим дисциплинам, так и глубину понимания профильных химических дисциплин.
К примеру, существует ряд работ [7, 8], в которых показаны практические возможности преподавать графические дисциплины – начертательную геометрию и инженерную графику – студентам – химикам и химикам-технологам.
В статье [7] предложен профессионально ориентированный на студентов-химиков подход к преподаванию начертательной геометрии. В частности, разделы, посвящённые симметрии, предложено изучать на примере кристаллографии, в раздел о пересечении поверхностей предложено внести диаграммы состояния. Также это позволяет ознакомить студентов с базовыми понятиями физической химии, что облегчит её изучение в дальнейшем.
В работе [8] предложен способ преподавания студентам направления «Химическая технология» курса Инженерная графика, ориентированного на приобретение первичных профессиональных навыков. Предложено выполнение задания по разработке и построению принципиальной технологической схемы химической установки. Такая практика может подготовить к выполнению курсовых и дипломных работ, а также к изучению технологических регламентов в будущей профессиональной деятельности.
Однако кроме разделов физической химии и различных областей химической технологии методы начертательной геометрии возможно соотнести со строением молекул высокомолекулярных и элементоорганических соединений.
Цель исследования: представить сложные для понимания области наук о высокомолекулярных и элементоорганических соединениях, связанные со строением их молекул, в качестве заданий по начертательной геометрии, которые возможно использовать как при преподавании начертательной геометрии для установления междисциплинарных связей, так и при объяснении строения макромолекул, металлоценовых соединений и ареновых комплексов переходных металлов на основе уже пройденного курса.
Материалы и методы исследования
Объектом исследования являются принятые модели строения макромолекул и металлоценовых соединений. В работе использованы классические методы начертательной геометрии: вращение, задание геометрических мест точек, пересечение поверхностей и фигур [9].
Результаты исследования и их обсуждение
Подход со стороны начертательной геометрии возможно использовать при рассмотрении структуры макромолекул для ознакомления студентов с моделями строения полимерной цепи и её характеристиками. Существует несколько моделей идеальной полимерной цепи [10]. Во всех моделях пренебрегают взаимодействием между звеньями, кроме непосредственно связанных, и заместителями. Сами по себе модели изначально описаны геометрически, их характеризуют рядом геометрических параметров: длиной связи, углом связи (смежным с валентным углом), торсионным углом.
В самой общей модели, цепи из свободно сочленённых сегментов, постоянна только длина связи. Она не представляет большого интереса с точки зрения начертательной геометрии, поскольку каждый атом цепи расположен в пространстве независимо от предыдущего, и валентный, и торсионный углы меняются. В модели цепи с фиксированным валентным углом и свободным вращением постоянными являются не только длина связей, но и валентные углы. При этом торсионный угол может меняться независимо. В модели с фиксированным валентным углом и заторможенным вращением возможность поворота на торсионный угол зависит от фактора Больцмана. В модели ротационно-изомерного состояния торсионный угол принимает только три значения: 0 ° (транс-состояние), 120 ° и –120 ° (гош-состояния).
Таким образом, в моделях с фиксированным валентным углом и свободным вращением, с фиксированным валентным углом и заторможенным вращением и ротационно-изомерного состояния структура цепи представлена одинаково, и они различаются только способом изменения торсионного угла. Изображение макромолекулы в рамках этих моделей приведено на рис. 1.
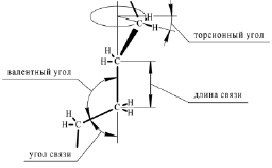
Рис. 1. Структура молекулы полиэтилена в рамках перечисленных идеальных моделей
Чтобы представить макромолекулу как задачу по начертательной геометрии, цепь необходимо показать как последовательность соединённых отрезков, в которых точки соответствуют атомам углерода, а длины всех отрезков в случае гомоцепных макромолекул равны и соответствуют длине связи между атомами в цепи. Поскольку в идеальных моделях взаимодействием между заместителями пренебрегают, то их изображение также не является обязательным в задаче. В моделях незначительно взаимодействие между звеньями в цепи, находящимися на большом расстоянии, поэтому построение более чем пяти звеньев не имеет смысла и, более того, излишне усложнит чертёж. При этом во всех трёх выбранных моделях валентный угол фиксирован, и поэтому отрезок, представляющий каждое последующее звено, будет двигаться по конической поверхности [11], на оси которой лежит предыдущий отрезок. Половина угла при вершине конуса будет смежной с валентным углом. Предложенный вид задачи и изображение такой структуры приведены на рис. 2.
Основным методом решения подобных задач будет вращение [9] сегментов цепи. Возможно создание подобных задач по теме «Модели строения макромолекул» по ряду направлений.
Направление 1: нахождение валентного угла или длины связи. В качестве исходных данных приведены 4–5 сегментов макромолекул в произвольном положении. Перед студентом стоит задача установить истинную длину связи или значение валентного угла, для чего необходимо повернуть сегменты таким образом, чтобы по крайней мере два из них лежали в горизонтальной или фронтальной плоскости уровня и их отображение стало истинным размером. Также возможно предложить студентам идентифицировать молекулу, приведя на том же чертеже изображения валентных углов или длин связей, соответствующих разным молекулам.
Направление 2: поворот на необходимый торсионный угол. Задачи направлены на поворот отрезков в заданное положение и хорошо сочетаются с моделями с заторможенным вращением или ротационно-изомерного состояния. Каждый из заданных сегментов макромолекул необходимо повернуть на определённый торсионный угол относительно предыдущего.
Направление 3: среднеквадратичное расстояние между концами цепи. Задачи позволяют наглядно познакомить студентов с понятием среднеквадратичного расстояния между концами цепи. Предложено повернуть сегменты таким образом, чтобы расстояние между концами цепи было минимальным или заданным. Также для простых случаев можно установить количество решений.
Соответственно, при использовании в профильно-ориентированном курсе начертательной геометрии на примере подобных задач можно закреплять тему «Вращение».
Для элементоорганических соединений с методами начертательной геометрии возможно соотнести строение ареновых комплексов переходных металлов и металлоценовых соединений – сандвичевых [12].
В этих комплексах связи многоэлектронные и многоцентровые, и длины связей между всеми атомами углерода в лигандах и металлом равны. Соответственно, как в ареновых ядрах, так и в пентадиениле длины С-С связей равны между собой. Структуры дибензолхрома как примера ареновых комплексов переходных металлов и ферроцена как металлоценового соединения приведены на рис. 3.
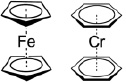
Рис. 3. Структуры дибензолхрома (справа) и ферроцена (слева)
Для представления сандвичевых соединений в качестве задач по начертательной геометрии атомы металлов и углерода в лигандах также можно представить как точки, заместителями следует пренебречь. Связи между точками-атомами представлены отрезками определённых длин. Поскольку длины связей между атомом металла и атомами углерода в лигандах равны, то атомы углерода будут лежать на сфере – геометрическом месте точек, удалённых на заданное расстояние от точки [13]. При этом центром сферы будет атом металла, радиус сферы равен длине связи между углеродом и металлом. Все атомы углерода в ароматическом кольце лиганда лежат в одной плоскости, также в случае шестичленного ароматического кольца положение атомов углерода удобно обозначить как точки на окружности, являющейся пересечением вышеупомянутой сферы и цилиндра [13], причём центр сферы лежит на оси цилиндра, радиус цилиндра равен длине С-С связи в арене. Предложенный вид задачи и изображение структуры приведены на рис. 4.
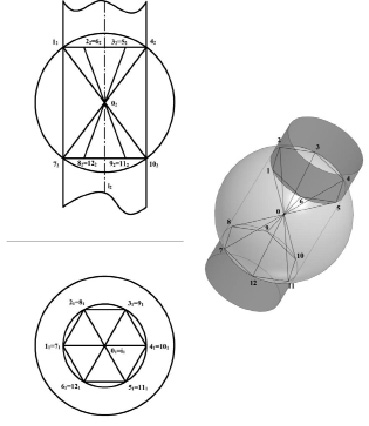
Рис. 4. Вид задачи (в проекциях на π1 и π2) и изображение геометрической структуры
Задачи возможно решить при знании геометрических мест точек и умении пересекать поверхности. Задачи по теме «Структура сандвичевых соединений» могут заключаться в достраивании молекул и определении длин связей С-С или С-Ме. В качестве исходных данных предложена группа точек. Алгоритм действия студентов следующий: во-первых, определить, какие из точек лежат в одной плоскости; во-вторых, определить форму ароматического кольца в этой плоскости (пятичленное, шестичленное) и достроить недостающие точки; в-третьих, найти точку, равноудалённую от всех точек – атом комплексообразователя.
В курсе начертательной геометрии эти задачи можно использовать для освоения темы «Геометрические места точек».
Заключение
Таким образом, предложены возможности междисциплинарной связи изучения структур высокомолекулярных и элементоорганических соединений с курсом начертательной геометрии. Предложены задачи, связанные со строением макромолекул, ареновых комплексов переходных металлов, металлоценовых соединений. Они могут быть использованы как в курсе начертательной геометрии для получения первичных профессиональных компетенций и знакомства с теоретическими основами этих разделов химии, так и в дисциплинах, связанных с высокомолекулярными и элементоорганическими соединениями, для освоения материала на основе уже пройденного курса.
В любом из вариантов использования такая междисциплинарная связь актуализирует полученные знания и повышает мотивацию и заинтересованность студентов.
Библиографическая ссылка
Киршанов К.А. ПОДХОД К ПРЕПОДАВАНИЮ СТРОЕНИЯ ВЫСОКОМОЛЕКУЛЯРНЫХ И ЭЛЕМЕНТООРГАНИЧЕСКИХ СОЕДИНЕНИЙ НА БАЗЕ КУРСА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ // Научное обозрение. Педагогические науки. 2019. № 6. С. 122-127;URL: https://science-pedagogy.ru/ru/article/view?id=2264 (дата обращения: 05.02.2026).
DOI: https://doi.org/10.17513/srps.2264


 science-review.ru
science-review.ru