science-review.ru
Формирование профессиональной компетенции обеспечивает развитие общих компетенций студентов. Организация обучения математическому моделированию процессов в компонентах природы предполагает учет потребностей, интересов и личностных особенностей обучаемого [1, 2]. Магистрант выступает как полноправный участник процесса обучения.
Цель исследования: изучение особенностей формирования профессиональных компетенций в процессе обучения математике на основе проектно-исследовательской деятельности.
Сельскохозяйственная мелиорация – это изменение природной среды с целью ее улучшения для ведения сельского хозяйства (Н.Ф. Реймерс, 1990). В образовательной программе магистратуры 20.04.02 «Природообустройство и водопользование», в КубГАУ по профилю подготовки «Мелиорация, рекультивация и охрана земель» предусмотрена дисциплина «Математическое моделирование процессов в компонентах природы». Дисциплина знакомит студентов с методами статистической обработки результатов почвенных исследований, полевых опытов.
Материалы и методы исследования
Рассматривая тему «Обработка материалов многолетних наблюдений», особое внимание уделяем модели парной линейной регрессии и методу наименьших квадратов (МНК) [3].
Пусть случайная величина Y (зависимая переменная, результативный признак) статистически зависит от случайной или неслучайной величины X (независимой, объясняющей переменной). Функция регрессии, как известно, определяется по формуле
φ(x) = M(Y/X = x).
Обозначение в правой части равенства подчеркивает, что речь идет о значении случайной величины Y, когда величина X приняла значение х [4]. Эти значения подчинены некоторому закону распределения, зависящему от х и с центром распределения M(yx) = φ(x). Таким образом, разность yx – φ(x) = ux есть случайная величина, для которой M(ux) = 0. Другими словами, случайную величину yx раскладываем на две составляющие: неслучайную φ(х) и случайный остаточный член ux, т.е.
yx = φ(x) + ux.
Последнее равенство выражает общую модель парной регрессии. Если известно, что φ(x) = a + βx, получим модель парной линейной регрессии
yx = α + βx1 + ux.
В рамках математической статистики законы распределений случайных величин нам неизвестны, но имеется ряд наблюдений, т.е. выборка объема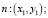 
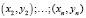, и тогда
yi = α + βx + ui.
В последней записи остаются неизвестными параметры а и β. По данным можно найти лишь оценки параметров а и β – соответственно a и b и получить выборочную оценку функции регрессии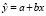 
, которую будем называть выборочной функцией регрессии
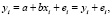
где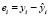 
называются остатками [5, 6].
Существует несколько методов получения оценок а и b. Метод наименьших квадратов (МНК) заключается в подборе таких a и b, чтобы сумма квадратов остатков была минимальной.
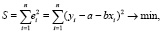
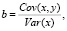
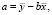
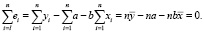
Далее рассматриваем условия Гаусса – Маркова.
Вернемся к исходной модели y = a + βx + u
Установим связь между оценкой b и параметром β
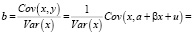
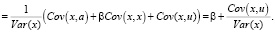
Здесь мы воспользовались свойством линейности ковариации по каждому аргументу и тем, что если один из аргументов ковариации есть постоянная величина, то ковариация равна нулю [7].
Действительно:
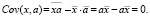
Оценка b – величина случайная, так как она состоит из двух слагаемых: β – величины неслучайной и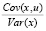 
– случайной величины (u – величина случайная по условиям модели).
Аналогично можно показать случайный характер оценки а. Чтобы получать достоверные результаты при использовании полученных оценок, последние должны удовлетворять ряду требований, например, несмещенности, состоятельности, эффективности (минимальности дисперсии).
Чтобы эти требования выполнить, при нахождении коэффициентов регрессии по МНК для модели yi = α + βxi + ui проверяют выполнение четырех условий Гаусса – Маркова [7–9]:
1-е условие: E(ui) = 0 для всех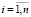 
. Это означает отсутствие систематического смещения у случайных членов во всех наблюдениях или, что 
.
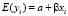2-е условие: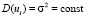 
. Дисперсия случайного фактора (ошибки) должна быть постоянна во всех наблюдениях. Это условие называется гомоскедастичностью. Случай, когда условие гомоскедастичности не выполняется, называется гетероскедастичностью. В условиях гетероскедастичности оценки, полученные по МНК, будут неэффективными.
3-е условие: cov(ui, uj) = 0 при i ≠ j. Это условие означает некоррелированность ошибок для разных наблюдений. Так как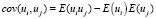 
, то при выполнения первого условия, третье можно записать в виде E(uiuj) = 0 при i ≠ j.
4-е условие: случайный член должен быть распределен независимо от объясняющих переменных, т.е.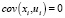 
. Так как E(ui) = 0, то
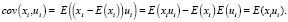
Следовательно, данное условие можно записать в виде E(xiui) = 0.
Четвёртое условие автоматически выполняется, если xi является детерминированной величиной, т.е. неслучайной.
При невыполнении данного условия оценки по МНК будут не только неэффективными, но и смещенными.
Докажем несмещенность оценок b и a в предположении, что х – детерминированная, т.е. неслучайная величина и, разумеется, выполнены остальные условия Гаусса – Маркова.
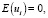то 
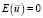и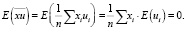 
Откуда
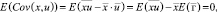
и
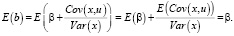
Несмещенность оценки b доказана.
Для оценки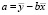 
заметим, что
,
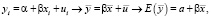
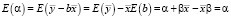что доказывает несмещенность оценки а.
Во втором условии утверждается, что дисперсия случайного члена в каждом наблюдении должна быть постоянной
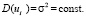
Это означает, что величина u примет какое-нибудь положительное или отрицательное значение с одинаковой для всех наблюдений вероятностью. Другими словами, величина u имеет одинаковый разброс, т.е. выполнено условие гомоскедастичности [10–12].
Если условие не выполняется, получим ситуацию гетероскедастичности, что означает неодинаковый разброс остатков. Гетероскедастичность приводит к тому, что оценки, найденные по МНК, хотя и останутся несмещенными, но будут неэффективными, т.е. существуют оценки с меньшей дисперсией, а применение t-статистики для определения значимости коэффициента регрессии может дать неверный результат.
Для модели yi = α + βxi + ui при выполнении условий Гаусса – Маркова оценки, полученные по методу наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
Заметим, что оценка называется линейной, если она линейно выражается через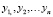 
. Оценки а и b, найденные по МНК, являются линейными.
Цель регрессионного анализа состоит в объяснении поведения зависимой переменной у. В результате построения выборочного уравнения регрессии каждое значение у разлагается на две составляющие
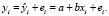
Величина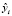 
– расчетное или спрогнозированное значение у в наблюдении i, а остаток ei есть расхождение между фактическим yi и спрогнозированным 
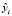. Это та часть, которая не объясняется с помощью уравнения регрессии. Разложим вариацию у на две составляющие: объясняемую уравнением регрессии и необъясняемую:
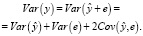
Используя ковариационные правила, найдём
.
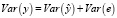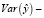часть вариации V(y), которая объясняется уравнением регрессии, Var(e) – необъясненная часть [13].
Коэффициент детерминации R2 определяет качество оценки и вычисляется по формуле
.
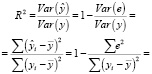
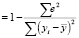И используется для оценки качества подбора линейной функции регрессии.
В линейной парной модели коэффициент детерминации R2 равен квадрату коэффициента корреляции между y и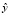 
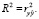
Коэффициент корреляции изменяется в пределах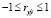 
и характеризует тесноту связи между y и 
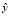. Коэффициент детерминации, следовательно, изменяется в пределах 0 ≤ R2 ≤ 1. Величина 1 – R2 характеризует долю дисперсии y, вызванную влиянием не учтенных в модели (случайных) факторов [14].
Результаты исследования и их обсуждение
Для проверки освоения материала магистрантам предлагаются типовые вопросы. Перед непосредственным выполнением заданий компьютерного тестирования необходимо внимательно изучить весь материал по данному блоку. Тестовые задания выполняются магистрантами самостоятельно без использования конспектов, учебников.
Типовые вопросы:
1. Что такое водопроницаемость почвы?
Ответ. Это способность почвы пропускать воду.
2. Что такое диффузия?
Ответ. Перенос растворенных веществ.
3. Чем вызвана диффузия?
Ответ. Градиентом концентрации раствора.
4. Почему закон распределения Пуассона называют законом редких событий?
Ответ. Так как закон распределения Пуассона описывает случайную величину (число наступлений события в n независимых опытах) при n достаточно большом и при вероятности наступления в каждом опыте p достаточно малом.
5. Статистические гипотезы делятся на:
Ответ. Параметрические и непара- метрические.
6. Что называют статистическим до- казательством?
Ответ. Процесс использования выборки для проверки гипотезы.
7. Какая гипотеза называется простой?
Ответ. Которая содержит только одно предположение.
8. В чем состоит ошибка второго рода при рассмотрении гипотез?
Ответ. Ошибка второго рода возникает тогда, когда нуль-гипотеза принимается, хотя на самом деле верна альтернативная гипотеза.
9. Какой используют критерий при проверке гипотезы о принадлежности двух выборок одной генеральной совокупности только на основании их средних?
Ответ.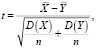 
n – объем выборки X, m – объем выборки Y.
10. В чем состоит различие графиков интегральной функции распределения дискретной и непрерывной случайных величин?
Ответ. График интегральной функции распределения дискретной случайной величины – разрывная (ступенчатая) кривая, для непрерывной случайной величины – непрерывная.
Изучение дисциплины «Математическое моделирование процессов в компонентах природы» завершается сдачей семестрового зачета. Зачет является формой итогового контроля сформированности компетенций, знаний и умений, полученных на практических занятиях и в процессе самостоятельной работы студентов.
Преподаватель имеет право принять у студента зачет и/или экзамен только при наличии первичных документов по учету результатов текущей и промежуточной аттестации. Первичными документами являются электронные журналы посещаемости и успеваемости по дисциплине, результаты тестирования. Все первичные документы должны передаваться в деканат преподавателем лично не позднее следующего дня после проведения испытания промежуточной аттестации.
Выводы
Преподавание дисциплины «Математическое моделирование процессов в компонентах природы» магистрантам, обучающимся по специальностям сельскохозяйственного профиля не только дает интеллектуальное развитие, но и несет пропедевтическую функцию для дальнейшего обучения и формирования профессиональных компетенций.
Таким образом, исследование показало, что пропедевтика формирования профессиональных компетенций в процессе обучения математике на основе проектно-исследовательской деятельности способствует повышению качества обучения. Внесение в образовательный процесс профессионально ориентированных задач по математике позволяет повысить уровень математической подготовки и осуществлять пропедевтику формирования профессиональных компетенций при подготовке специалистов-мелиораторов.
Представленные в данной статье методы формирования компетенций направлены на повышение качества высшего образования и эффективности образовательного процесса и могут быть использованы в образовательном процессе других дисциплин естественно-математического цикла.
Библиографическая ссылка
Сафронова Т.И., Степанов В.И. ФОРМИРОВАНИЕ ПРОФЕССИОНАЛЬНЫХ КОМПЕТЕНЦИЙ ПРИ ИЗЛОЖЕНИИ ДИСЦИПЛИНЫ «МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В КОМПОНЕНТАХ ПРИРОДЫ» // Научное обозрение. Педагогические науки. – 2019. – № 6. – С. 48-52;URL: https://science-pedagogy.ru/ru/article/view?id=2248 (дата обращения: 19.04.2024).