Современное строительство уже нельзя представить без внешней архитектурной отделки здания, а также изысканных и весьма лаконичных интерьеров. Элементы архитектурной отделки зданий, некоторые принципы внутренней отделки жилища, а также предметы интерьера могут использовать деление угла на три равные части. Задача о делении угла берёт своё начало в 5 веке до нашей эры, когда необходимо было разделить угол на три равные части для сооружений архитектуры и строительной техники. Эта задача прошла долгий путь и в 1837 году французский математик Ванцель П.Л. доказал её классическую неразрешимость, то есть при помощи циркуля и линейки. Однако при помощи некоторых механизмов, основанных на геометрическом равенстве трёх углов, можно разделить произвольный угол на три равные части. Такие механизмы, называемые трисекторами, могут быть весьма полезными, а иногда необходимыми для решения задач планирования и сооружения отдельных элементов интерьера или необычных форм здания. Рассмотрим основные трисекторы и их принципы действия.
Трисекция угла при помощи линейки Невиса
Имеется угол Ðα = ÐPOM. Необходимо построить угол ∠β, величина которого втрое меньше данного: ∠α = ∠3β (рис. 1).
Продолжим сторону OM исходного угла α и построим на ней окружность произвольного радиуса a, и центром в точке O. Стороны угла пересекаются с окружностью в точках P и M. Возьмём линейку Невиса, отложив на ней длину радиуса a, и построим отрезок AB. Получим угол ∠PAM равный одной трети исходного угла ∠α [1] Этот способ является одним из самых известных, однако далеко не самым удобным.
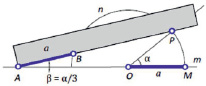
Рис. 1. Деление угла при помощи линейки Невиса
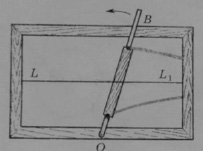
Рис. 2. Конхоидограф
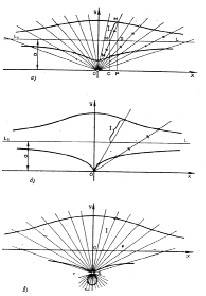
Рис. 3. Конхоиды Никомеда
Конхоида Никомеда
В 3 веке до н.э. древнегреческий математик Никомед придумал любопытную кривую. Рассказав об этой кривой, Прокл Диадох назвал её Конхоидой (от греч. «конхе» – раковина). С помощью этой кривой Никомед разделил острый угол на три равные части (рис. 3). Для построения конхоиды Никомед сконструировал прибор – «Конхоидограф» (рис. 2). Конхоидограф представляет собой рамку, в которой натянута проволока (LL1), и рейка (OB), закреплённая с одной стороны, по которой перемещается втулка с закреплёнными карандашами. Втулка так же ходит по проволоке (LL1) [2, 3].
Механизм Декарта
Французский математик Рене Декарт сконструировал механическое приспособление, позволяющее производить трисекцию угла (рис. 4). В этом механизме шарниры O, A, B, C и D закреплены и не могут передвигаться по рейкам, а шарниры E и F свободно передвигаются вдоль реек OE и OF. Необходимые условия: OA=OB=OC=OD и AE=CE=BF=DF [2]. Данный механизм достаточно прост в изготовлении, использовании и имеет довольно большой интервал деления угла. Минимальное и максимальное значение угла напрямую зависит от размеров инструмента и соотношения его основных сторон элементов между собой.
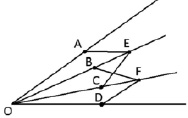
Рис. 4. Схема механизма Декарта
Шарнирный трисектор
Представляет собой антипараллелограмм ABCD (рис. 5), к которому прикреплены ещё два подобных антипараллелограмма AFHB и AMLF (рис. 6, 7) [4]. Этот механизм интересен тем, что, используя такой алгоритм построения, можно разделить угол не только на 3 части, но и на 4,5 и более частей (рис. 8).
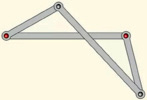
Рис. 5. Антипараллелограмм
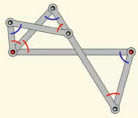
Рис. 6. Прикрепление подобного антипараллелограмма
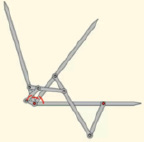
Рис. 7. Шарнирный трисектор
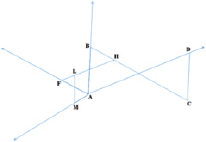
Рис. 8. Схема шарнирного трисектора
Простейший трисектор из картона
Данный трисектор состоит из нескольких геометрических фигур, расположенных так, что некоторые их элементы находятся в прямой зависимости друг между другом. Рассмотрим его подробнее (рис. 9): AB = BO (BO – радиус окружности O). BD – имеет неограниченную длину. Помещать трисектор следует так, чтобы вершина угла S находилась на линии BD, одна сторона угла прошла через точку A, а другая сторона коснулась полукруга [5].
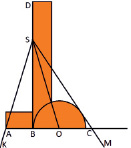
Рис. 9. Картонный трисектор и принцип его действия
Собственный трисектор
В процессе исследовательской работы были рассмотрены различные способы и виды трисекторов и, поняв принципы действия существующих трисекторов, был сконструирован собственный трисектор. Его конструкция схожа с механизмом Декарта, однако этот трисектор имеет конструктивные отличия (рис. 10). В этом механизме шарниры O, A, B, C, D закреплены не подвижно, а шарниры E и F передвигаются вдоль реек OB и OC. Также как в механизме Декарта и шарнирном трисекторе минимальное и максимальное значение исходного угла, который требуется разделить, зависит от размеров и соотношения сторон инструмента.
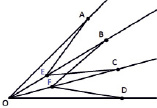
Рис. 10. Схема собственного трисектора
Программа для трисекции угла
Так как мы живём в эпоху электронно-вычислительной техники, то для удобства и увеличения точности трисекции угла была написана программа, которая позволяет разделить произвольный угол на три равные части и вывести графическое изображение разделённого угла на экран монитора, с которого впоследствии уже можно распечатать данное изображение на принтере, и тем самым выполнить деление угла (рис. 11, 12). Программа написана на языке программирования Pascal с использованием графического модуля GraphABC.
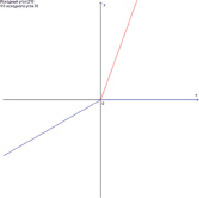
Рис. 11. Пример 1 деления угла в программе
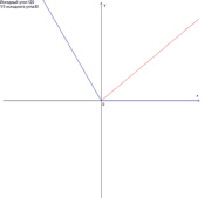
Рис. 12. Пример 2 деления угла в программе
Применение трисекции угла
Проведя теоретическое исследование и освоив принцип действия выше представленных приспособлений, их дальнейшее практическое применение возможно в следующих областях (рис. 13).

Рис. 13. Примеры применения трисекции угла в строительстве
– Планирование и сооружение эркеров в зданиях;
– Планирование и сооружение сложных геометрических форм зданий;
– Проектирование и возведение винтовых лестниц, в которых ступенькой является треугольник. Однако число ступеней должно быть равно следующим числам: 3, 6, 9, 12, 18, 24, 27, 36 и далее, однако на большее число ступеней делить лестницу не целесообразно;
– Проектирование и производство фигурного паркета или нанесение на паркет рисунка.
Библиографическая ссылка
Храмовских М.А. ТРИСЕКЦИЯ УГЛА КАК ХОРОШО ЗАБЫТЫЙ ИНСТРУМЕНТ В СТРОИТЕЛЬСТВЕ И БЛАГОУСТРОЙСТВЕ ЗДАНИЙ // Научное обозрение. Педагогические науки. 2019. № 4-3. С. 79-83;URL: https://science-pedagogy.ru/ru/article/view?id=2125 (дата обращения: 11.03.2026).


 science-review.ru
science-review.ru