science-review.ru
Для создания экономически развитого общества, активного продвижения научно-технического прогресса особая роль отводится высшей математике. Современные ученые используют для исследования экономических процессов методы математического анализа, регрессионного анализа, теории игр, линейного программирования, матричного и векторного исчислений и т.п., которые в свою очередь являются составляющими математического моделирования. Одним из важнейших разделов математики, который имеет большое прикладное значение, является раздел «Обыкновенные дифференциальные уравнения». Кроме общематематического и теоретического интереса, дифференциальные уравнения находят широкое практическое применение. Например, при решении задач, связанных с оптимальным управлением, экономической деятельностью фирмы или предприятия, организацией производственного процесса и т.д. В виде дифференциальных уравнений записываются соотношения между экономическими переменными, такими как цены, заработная плата, капитал, процентная ставка и др.
Основу экономической теории составляют экономические законы, выраженные в виде количественных соотношений между величинами, характеризующими экономическую систему, или процесс. Такие законы дают возможность исследовать реальные экономические системы на основе математических моделей. Построение и изучение этих моделей составляет предмет математической экономики, которая рассматривает экономику как сложную динамическую систему.
В исследовании метод моделирования является важнейшим универсальным методом. Модель – «это объект или явление, аналогичные, т.е. в достаточной степени повторяющие свойства моделируемого объекта или явления (прототипа), существенные для целей конкретного моделирования, и опускающие несущественные свойства, в которых они могут отличаться от прототипа» [1]. Модель какой-либо сложной системы тоже представляет собой систему (и нередко весьма сложную), имеющую физическое воплощение либо записанную с помощью слов, цифр, математических обозначений, графических изображений и т. д. Таким образом, можно сказать, что модель – это физическая или знаковая система, имеющая объективное подобие с исследуемой системой в отношении функциональных, а часто и структурных характеристик, являющихся предметом исследования.
Математическая модель представляет собой совокупность уравнений, неравенств, функционалов, логических условий и других соотношений, отражающих взаимосвязи и зависимости основных характеристик моделируемой системы. Однако важное преимущество модели состоит в том, что необъятная с точки зрения полного описания реальная социально-экономическая система заменяется пусть даже непростой, но вполне доступной для анализа и расчетов моделью, которая вместе с тем сохраняет в себе все существенное, что интересует исследователя. Это существенное выступает в модели даже более четко и рельефно, не будучи затемнено всевозможными незначащими частностями и деталями, посторонними и случайными факторами. Модель, возникшая в результате построения, позволяет исследователю экспериментировать с различными параметрами, переменными величинами, условиями и ограничениями и выяснять, к каким возможным результатам это приводит [2].
Для изучения математических моделей экономики, помимо экономической науки, необходимо владеть математическими методами, среди которых аппарат дифференциальных уравнений играет важную роль. Экономические закономерности, как правило, представляют собой сложные нелинейные соотношения между экономическими величинами, явный вид которых непосредственно установить затруднительно. При наличии устойчивой закономерности малые изменения величин можно приближенно заменить дифференциалами. Тогда нелинейные соотношения между величинами, соответственно, заменяются более простыми линейными соотношениями между величинами и их производными. Эти соотношения представляют собой дифференциальные уравнения, с помощью которых строится математическая модель экономической системы или процесса.
Примеры моделей экономических процессов, основу которых составляют дифференциальные уравнения, приведем по сложности используемых уравнений (от простых к сложным). Рассмотрим модели процессов, в которых возникает необходимость использования теории дифференциальных уравнений с разделяющимися и разделёнными переменными. К задачам такого типа относятся, например, задачи об эффективности рекламы, изменении численности населения, зависимость спроса или предложения от цены товара, зависимость функции спроса от эластичности, истощение ресурсов Земли или рост населения, рост денежного вклада в банке и другие.
Пример 1. (Эффективность рекламы). Фирма подготовила для реализации новый продукт. Для его продвижения была проведена рекламная компания, в результате которой о новинке из 10000 потенциальных покупателей узнали 2500 человек. После этого сведения о новом товаре распространяются с помощью передачи информации от одного человека к другому. Обозначим через x(t) число покупателей, знающих о новинке в момент времени t. Изменение этой величины будет пропорционально как числу покупателей, знающих о новинке, так и не знающих о ней, а также промежутку времени dt, за который это изменение происходит, то есть dx = kx(n – x)dt, где п – общее число потенциальных покупателей новинки (в нашем случае п = 10000), k – коэффициент пропорциональности (будем считать, что k = 2?10-6 чел./день), n – x – число покупателей, не знающих о новинке (n – x = 10000 – 2500 = 7500) Используя уравнение логистической кривой [3], получим зависимость x(t) с учетом данных нашей задачи:
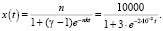
Предположим, что t = 20 дней, тогда x(20) = 3321, т.е. за 20 дней о новинке будут знать приблизительно 3321 покупатель.
Допустим теперь, что t = 30, тогда о новинке будут знать приблизительно x(20) = 3778 покупателей. Таким образом, за 30 дней о новинке будут знать 6278 человек.
Пример 2. (Спрос и предложение). Спрос и предложение – экономические категории товарного производства, возникающие и функционирующие на рынке, в сфере товарного обмена. Рассмотрим какой-нибудь товар. Обозначим через p цену на товар, а через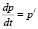 
– так называемую тенденцию формирования цены (производную цены во времени). Рассмотрим случай, когда спрос и предложение зависят от скорости изменения цены [3, с. 10]. В зависимости от разных факторов спрос и предложение могут быть различными функциями цены и тенденции формирования цены. Одним из экономических законов товарного производства является закон спроса и предложения, который заключается во взаимозависимости спроса и предложения и их объективном стремлении к соответствию. Для экономики представляет интерес условие, при котором спрос равен предложению, т.е. s(p, p/) = q(p, p/). При этом цена p = p0 называется равновесной. Обе функции s и q являются линейными относительно переменных р и р/. Следовательно, решение задач на спрос и предложение приводит к необходимости использования теории линейных дифференциальных уравнений первого порядка. Описание методов решения таких уравнений можно найти в [4].
Например, функции спроса и предложения имеют вид:
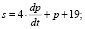
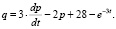
Равновесие между спросом и предложением сохраняются при условии при условии
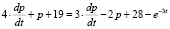
или, когда выполняется равенство
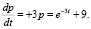(1)
В результате получено линейное неоднородное дифференциальное уравнение первого порядка с постоянными коэффициентами. Для его решения применим метод И. Бернулли: общее решение ищем в ви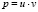де 
, где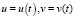 
. Тогда 
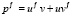. Подставляя р и р/ в (1), приходим к уравнению
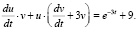(2)
Ищем v:
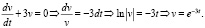
Подставляя найденное значение v в уравнение (2), найдем и:
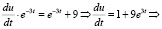
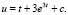
Общее решение уравнения (1) запишется в виде
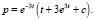
Найдем зависимость равновесной цены от времени, если в начальный момент p = 23:
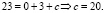
Таким образом, искомая зависимость имеет вид
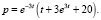
Чтобы узнать является ли данная равновесная цена устойчивой, найдем limt→∞ p при этом получающуюся в ходе вычислений неопределённость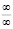 
будем раскрывать по правилу Лопиталя.
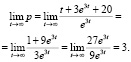
Следовательно, равновесная цена является устойчивой.
Пример 3. (Модель рынка с прогнозируемыми ценами). В данной модели используется теория линейных дифференциальных уравнений второго порядка. Обычно в простых моделях рыночной экономики спрос и предложение зависят от текущей цены на товар. Однако в реальных ситуациях существует зависимость от тенденции ценообразования и темпов изменения цены. В моделях с непрерывными и дифференцируемыми по времени t функциями эти характеристики описываются соответственно первой и второй производными функции цены p(t). Например, пусть функции спроса s(t) и предложения q(t) имеют следующие зависимости от цены р:
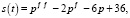
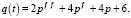
Принятые зависимости реалистичны, так как если темп цены растет (р// > 0), то интерес к товару на рынке то же растет и наоборот, если темп цены падает, то и интерес к товару падает. Причем быстрый рост цены отпугивает покупателя, поэтому слагаемое с первой производной функции цены входит со знаком минус. В то же время темп изменения цены влияет на усиление предложения (рост цены увеличивает предложение), поэтому слагаемое, содержащее р/, входит в q(t) со знаком плюс. Установим зависимость цены от времени. Воспользуемся, как и в предыдущем примере, условием равновесного состояния рынка s(t) = q(t). Исходя из этого условия, получаем уравнение
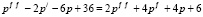
или
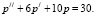(3)
Получено линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его общее решение складывается из общего решения соответствующего однородного уравнения и частного решения данного неоднородного уравнения [5, с.73-81].
Общее решение однородного уравнения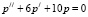 
найдем исходя из вида корней характеристического уравнения
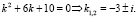
Так как корни характеристического уравнения являются комплексными, то общее решение однородного уравнения имеет вид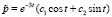 
, где c1 и c2 – произвольные постоянные.
В качестве частного решения возьмем постоянную установившуюся цену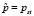 
. Подставляя это значение в формулу (3), найдем, что 
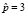. Таким образом общее решение уравнения (3) имеет вид: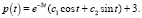 
Учитывая, что
,
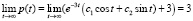делаем заключение: все интегральные кривые имеют горизонтальную асимптоту p = 3. Это означает, что все цены стремятся к устоявшейся цене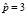 
с колебаниями около неё, причем амплитуда колебаний затухает со временем.
Из рассмотренных задач можно сделать вывод, что методы моделирования с помощью дифференциальных уравнений широко применяются для решения экономических задач. Анализ полученных общих и частных решений позволяет выявить резервы повышения эффективности производства, установить зависимости между спросом и предложением.
Библиографическая ссылка
Кукленкова А.А. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В МОДЕЛИРОВАНИИ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ // Научное обозрение. Педагогические науки. – 2019. – № 4-3. – С. 60-63;URL: https://science-pedagogy.ru/ru/article/view?id=2120 (дата обращения: 20.04.2024).