Математические исследования в сфере экономики прямо определяют возможности построения экономических моделей, концепций и вообще движение экономической мысли. Использование математических методов и их приложений в экономических исследованиях помогает экономистам разных категорий анализировать различные факты экономической жизни общества, как на макроэкономическом уровне, так и на микроэкономическом. Анализ экономической действительности по средствам математических методов позволяет строить более эффективные экономические модели, чтобы впоследствии применять их на практике, избегая множества проб и ошибок. Одним из наиболее часто использующихся математических методов является корреляционный анализ, появившийся в результате потребности экономической теории в определении связи между двумя событиями, и в определении степени взаимовлияния этих событий друг на друга [1, 2].
Корреляционный анализ – широко известный и эффективный метод математической статистики, позволяющий по совокупности значений показателей выявлять и описывать связи между показателями.
Так, если изменение одной из переменных сопровождается изменениями условного среднего значения другой переменной величины, то такая зависимость является корреляционной [3].
Корреляционный анализ рассматривает две основные задачи:
1) Первая задача корреляции – выявление на основе наблюдений за большим количеством факторов того, как изменяется в среднем результативный признак в связи с изменением факториального признака.
2) Вторая задача корреляции – состоит в определении степени тесноты связи коэффициента корреляции.
Корреляционной зависимостью У от X называют функциональную зависимость условной средней ух от x: ух = f (x). Это уравнение называют уравнением регрессии У на X; функцию f (x) называют регрессией У на X, а ее график – линией регрессии У на X.
При выявлении влияния одних признаков на другие выделяют два признака: факториальный и результативный [4, 5].
Например, уровень заработной платы – факториальный признак, а производительность труда – результативный.
Коэффициент корреляции: это математический показатель, использующийся для определения тесноты связи между двумя величинами при прямолинейной зависимости.
Коэффициент корреляции обозначается буквой r и определяется по формуле:
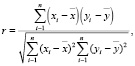
где 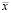 ,
, 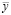 – выборочные средние.
– выборочные средние.
После выявления коэффициента корреляции необходимо его проанализировать и сделать выводы о тесноте связи. В этом помогут свойства коэффициента корреляции [6].
Свойства коэффициента корреляции r
– r изменяется в интервале от –1 до +1.
– Знак r означает, увеличивается ли одна переменная по мере того, как увеличивается другая (положительный r), или уменьшается ли одна переменная по мере того, как увеличивается другая (отрицательный r).
– Величина r указывает, как близко расположены точки к прямой линии. В частности, если r = +1 или r = –1, то имеется абсолютная (функциональная) корреляция по всем точкам, лежащим на линии (практически это маловероятно); если r ≅ 0, то линейной корреляции нет (хотя может быть не линейное соотношение). Чем ближе r к крайним точкам (±1), тем больше степень линейной связи [7].
– Коэффициент корреляции r безразмерен, т.е. не имеет единиц измерения.
– Величина r обоснована только в диапазоне значений x и y в выборке. Нельзя заключить, что он будет иметь ту же величину при рассмотрении значений x или y, которые значительно больше, чем их значения в выборке.
– x и y могут взаимозаменяться, не влияя на величину r (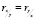 )
)
– Корреляция между x и у не обязательно означает соотношение причины и следствия.
– r2 представляет собой долю вариабельности у, которая обусловлена линейным соотношением с x.
Регрессия – одно из основных понятий в теории вероятности и математической статистике, выражающее зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин. Данную зависимость можно, наглядно, увидеть построив прямую регрессии.
Прямая регрессии – это та линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию связи [8].
Прямая регрессии должна отображать изменение средних величин результативного признака (y) по мере изменения величин факторного признака (x) при условии полного взаимопогашения всех прочих – случайных по отношению к фактору (x) – причин. Для построения прямой регрессии необходимо составить уравнение регрессии.
Уравнение регрессии – это уравнение, представляющее отношение между значениями одной переменной (х) и наблюдаемыми значениями другой (у).
При построении уравнения регрессии нам должен быть известен такой показатель как коэффициент регрессии [9].
Этот коэффициент показывают интенсивность влияния факторов на результативный показатель.
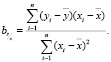
Рассмотрим одну из наиболее часто встречающихся практических задач, использующих в решении регрессионный анализ.
Таблица 1
|
Фабрики по производству игрушек |
||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
X |
10 |
14 |
21 |
23 |
27 |
32 |
39 |
45 |
55 |
61 |
62 |
68 |
|
Y |
3,8 |
4,8 |
5,9 |
6,1 |
6,2 |
6,3 |
6,6 |
7,4 |
8,5 |
9,7 |
10,5 |
12,4 |
Пусть имеются данные средней производительности труда на одного рабочего y (тыс. руб.) и объема выпуска товара x (тыс. руб.) на 12 фабриках, производящих мягкие игрушки (табл. 1). На основании данных планового отдела предприятий требуется:
1) Определить зависимость (коэффициент корреляции) средней производительности труда на одного рабочего от объема выпуска товара.
2) Составить уравнение прямой регрессии этой зависимости.
При решении данной задачи мы можем увидеть, что связь между изучаемыми признаками может быть выражена уравнением прямой линии регрессии Y на X: 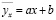 . Для вычисления параметров a, b и коэффициента корреляции составим расчетную таблицу (табл. 2).
. Для вычисления параметров a, b и коэффициента корреляции составим расчетную таблицу (табл. 2).
Таблица 2
|
Фабрики по производству игркушек |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||
|
X |
10 |
14 |
21 |
23 |
27 |
32 |
39 |
45 |
55 |
61 |
62 |
68 |
457 |
|
Y |
3,8 |
4,8 |
5,9 |
6,1 |
6,2 |
6,3 |
6,6 |
7,4 |
8,5 |
9,7 |
10,5 |
12,4 |
88,2 |
|
X^2 |
100 |
196 |
441 |
529 |
729 |
1024 |
1521 |
2025 |
3025 |
3721 |
3844 |
4624 |
21779 |
|
Y^2 |
14,44 |
23,04 |
34,81 |
37,21 |
38,44 |
39,69 |
43,56 |
54,76 |
72,25 |
94,09 |
110,3 |
153,8 |
716,3 |
|
XY |
38 |
67,2 |
123,9 |
140,3 |
167,4 |
201,6 |
257,4 |
333 |
467,5 |
591,7 |
651 |
843.2 |
3882,2 |
Параметры a, b найдем из системы уравнений
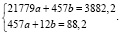
Получаем a = 0,12, b = 2,8, тогда уравнение регрессии принимает окончательный вид: 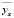 = 0,12x + 2,8.
= 0,12x + 2,8.
Данному уравнению можно дать геометрическую иллюстрацию (рисунок).
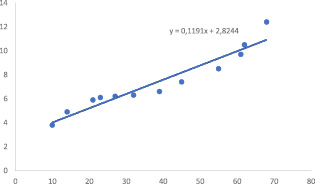
Графическое построение уравнения регрессии
Найдем выборочный коэффициент корреляции:
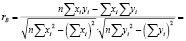
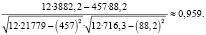
Итак, после проведенных исследований можно увидеть что, между объемом выпуска товаров x и производительностью труда y на фабриках по производству игрушек существует сильная положительная корреляционная связь. И это значит что, производительность труда полностью влияет на объем выпуска товаров. И если будут прослеживаться изменения в производительности труда, то они повлекут за собой изменения объема выпуска.
На основании вышеизложенного можно сказать, что методы корреляционного анализа находят широкое применение во всех разделах экономики. Это может быть и оценка взаимосвязи между международными фондовыми рынками, и определение влияния различных производственных отраслей на общую конъюнктуру рынка, и выявление связи между производительностью труда и объемом выпуска товаров.
Библиографическая ссылка
Долгополова А.Ф., Проказин А.А. ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ В ЭКОНОМИЧЕСКИХ РАСЧЕТАХ // Научное обозрение. Педагогические науки. 2019. № 4-3. С. 56-59;URL: https://science-pedagogy.ru/ru/article/view?id=2119 (дата обращения: 11.03.2026).


 science-review.ru
science-review.ru