Постановка задачи. Определим форму свободной поверхности магнитной жидкости, располагающейся вокруг вертикального полого цилиндра с бесконечно большой магнитной проницаемостью. Будем считать цилиндр безмерно длинным. Магнитное поле в удалении от цилиндра однородное. Вектор приложенного внешнего неизменного магнитного поля 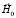 ориентирован перпендикулярно оси цилиндра и вектору силы тяжести.
ориентирован перпендикулярно оси цилиндра и вектору силы тяжести.
Уравнения данной задачи [1–3] в приближении феррогидродинамики- это уравнение (1) магнитного поля Н для областей пространства, занятых непосредственно магнитной жидкостью и уравнения равновесия магнитной жидкости.
Уравнение равновесия:
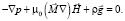 (1)
(1)
В данном случае m = m(Н) – относительная магнитная проницаемость магнитной жидкости, р – давление в магнитной жидкости, 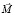 – вектор намагниченности магнитной жидкости.
– вектор намагниченности магнитной жидкости.
Раздел магнитная жидкость – воздух, на свободной поверхности, приводит к соответствию:
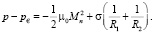 (2)
(2)
Тут ра – давление в воздухе, р – давление в магнитной жидкости вблизи границы раздела магнитная жидкость - воздух, Mn - нормальная компонента намагниченности на свободной плоскости магнитной жидкости, s – поверхностное натяжение, R1 и R2 – главные радиусы кривизны поверхности магнитной жидкости.
Из этого следует уравнение свободной поверхности магнитной жидкости:
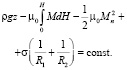 (3)
(3)
Здесь z – вертикальная координата.
При намагниченности магнитной жидкости, имеющей порядок величины Ms ≈ 104 A/м, поверхностном натяжении магнитной жидкости s ≈ 10-2 Н/м, специфических радиусах кривизны R1 и R2 ≈ 10-3 м, имеют соответственно порядки величин 102: 10 : 1. [4, 5].
Учитывая данную характеристику, уравнение (3) для свободной поверхности магнитной жидкости представится в следующем виде:
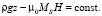 (4)
(4)
Подставляя в уравнение (4) поле (5) полого цилиндра:
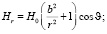
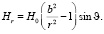 (5)
(5)
Найдем выражение для формы свободной поверхности магнитной жидкости, охватывающую наружную часть полого цилиндра:
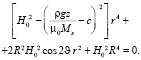 (6)
(6)
Задавая в (6) z меняющиеся от 0 до L (L - длина цилиндра), получим биквадратное уравнение для r от J, окружающее форму сечения объема магнитной жидкости плоскостью z = const.
Графики указанных сечений, когда размер внешнего магнитного поля равен H0 = 105 кА/м, при разных значениях z и с показаны на рис. 1, а–в. Направление магнитного поля 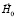 представлено на фигурах стрелкой. На рисунках продемонстрированы картины размещения свободной поверхности магнитной жидкости для первого квадранта плоскости сечения z = const. Кривые на рис. 1, а– в – геометрические места точек, описываемых уравнением (6) при значениях
представлено на фигурах стрелкой. На рисунках продемонстрированы картины размещения свободной поверхности магнитной жидкости для первого квадранта плоскости сечения z = const. Кривые на рис. 1, а– в – геометрические места точек, описываемых уравнением (6) при значениях 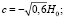
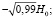
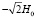 соответственно. Линии 1, 2, 3 на данных фигурах построены для значений параметра z = 0, z = 0,01 м, z = 0,02 м соответственно.
соответственно. Линии 1, 2, 3 на данных фигурах построены для значений параметра z = 0, z = 0,01 м, z = 0,02 м соответственно.
а) б)
в)
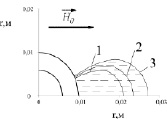
Рис. 1. а. Фигура равновесия свободной поверхности магнитной жидкости, в однородном внешнем магнитном поле 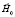 , полученные из уравнения (6) при
, полученные из уравнения (6) при 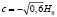 . Линии 1, 2, 3 – границы свободной поверхности жидкости вблизи верхнего торца, среднего сечения и нижнего торца цилиндра. б. Фигура равновесия свободной поверхности магнитной жидкости, в однородном внешнем магнитном поле
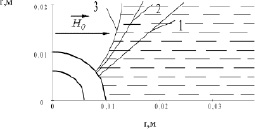
. Линии 1, 2, 3 – границы свободной поверхности жидкости вблизи верхнего торца, среднего сечения и нижнего торца цилиндра. б. Фигура равновесия свободной поверхности магнитной жидкости, в однородном внешнем магнитном поле 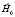 , полученная путем расчета по уравнению (6) при
, полученная путем расчета по уравнению (6) при 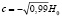 . Линии 1, 2, 3 соответствуют границе жидкости вблизи верхнего торца, среднего сечения и нижнего торца цилиндра. в. Фигура равновесия свободной поверхности магнитной жидкости, в однородном внешнем магнитном поле
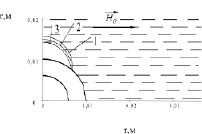
. Линии 1, 2, 3 соответствуют границе жидкости вблизи верхнего торца, среднего сечения и нижнего торца цилиндра. в. Фигура равновесия свободной поверхности магнитной жидкости, в однородном внешнем магнитном поле 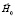 , полученная путем расчета по уравнению (6) при
, полученная путем расчета по уравнению (6) при 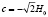 . Линии 1, 2, 3 соответствуют границе жидкости вблизи верхнего торца, среднего сечения и нижнего торца цилиндра
. Линии 1, 2, 3 соответствуют границе жидкости вблизи верхнего торца, среднего сечения и нижнего торца цилиндра
На рис. 1, а изображено расположение свободной поверхности магнитной жидкости, когда цилиндр охватывал малый объем магнитной жидкости.
Штриховкой на рис. 1, а, представлена зона, занятая магнитной жидкостью. Примечательно, что сечение объема магнитной жидкости плоскостью z = const возрастает в направлении силы тяжести (от линии 1 к линии 3).
На рис. 1, б, наибольшему объему магнитной жидкости в кювете соответствует, объем магнитной жидкости в сечении плоскостью z = const. Линии 1, 2 являются границей раздела магнитная жидкость -воздух в плоскости верхнего торца цилиндра в сечении z = 0 и в среднем сечении цилиндра z = 0,01 м. Указанные штриховкой области, заняты магнитной жидкостью. За пределами - воздух. Границей раздела магнитная жидкость- воздух является линия 3.
С увеличением объема магнитной жидкости, в магнитной жидкости, охватывающий цилиндр, образуются две сужающиеся книзу воронки – воздушные полости, что и показано на рис. 1, в.
Не заштрихованная зона, ограниченная линиями 1, 2, 3, не занята магнитной жидкостью.
Заштрихованная область занята жидкостью. Сформировавшаяся воронка, сужается в направлении силы тяжести.
Таким образом, расчеты демонстрируют, что с сокращением параметра с область свободная от магнитной жидкости на дне кюветы, уменьшается до вырождения. Вершина воронки поднимается в направлении верхнего торца цилиндра [6, 7].
В процессе данной работы, проводился эксперимент, в котором рассматривалось, распределение свободной поверхности магнитной жидкости в окрестности наружной и внутренней поверхностей полого ферромагнитного.
Полый ферромагнитный цилиндр с высотой, равной наружному диаметру, располагался на дне немагнитной цилиндрической кюветы. Состав масштаба полого цилиндра, используемого в описываемом эксперименте: наружный диаметр и высота 20 мм, внутренний диаметр 12 мм. Размеры кюветы: диаметр 100 мм, высота 70 мм. Дном кюветы являлось матовое стекло. Используемая система кюветы позволяла совершать подсветку снизу, что обеспечивало более контрастное выделение границы растекшейся по дну кюветы магнитной жидкости.
Фотография образца при виде сверху, показана на рис. 2. Для более удобной характеристики областей, в окрестности которых жидкость по-разному прилегает к верхней части цилиндра, введем угол J – угол между направлением внешнего приложенного магнитного поля 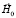 и направлением радиус-вектора r, проведенного из точки, расположенной на оси цилиндра в плоскости поперечного сечения, до определенной точки внешней поверхности цилиндра. Далее будем называть области поверхности цилиндра, для которых угол J равен 0 ° или 180 ° – полюсами цилиндра, а участки поверхности цилиндра, для которых угол J составлял ±90 ° – боковыми участками поверхности цилиндра.
и направлением радиус-вектора r, проведенного из точки, расположенной на оси цилиндра в плоскости поперечного сечения, до определенной точки внешней поверхности цилиндра. Далее будем называть области поверхности цилиндра, для которых угол J равен 0 ° или 180 ° – полюсами цилиндра, а участки поверхности цилиндра, для которых угол J составлял ±90 ° – боковыми участками поверхности цилиндра.
Округлый просвет полости цилиндра, виден в центре рис. 2. В поперечном сечении столбики магнитной жидкости приобретают форму, близкую к эллиптической. Боковые поверхности цилиндра полностью свободны от магнитной жидкости.

Рис. 2. Фотография полого цилиндрического образца, окруженного магнитной жидкостью суммарным объемом 2,6 см3

Рис. 3. Фотография полого цилиндрического образца, окруженного магнитной жидкостью суммарным объемом 54 см3
При последующем увеличении объема магнитной жидкости в кювете (рис. 3) лужицы в придонной части столбиков магнитной жидкости в окрестности полюсов цилиндра растекаются непосредственно по дну кюветы в направлении полюсов электромагнита. Высота столба жидкости на удалении от цилиндра более, чем на величину его диаметра, в направлении полюсов электромагнита увеличивается. Но, боковые части поверхности цилиндра остаются свободными от магнитной жидкости. Сохраняется неизменной и ширина раскрытия полосок боковой поверхности цилиндра, свободной от магнитной жидкости. Описываемые области боковой поверхности цилиндра, свободные от магнитной жидкости.

Рис. 4. Фотография полого цилиндрического образца, окруженного магнитной жидкостью суммарным объемом 159 см3
При достижении суммарного объема магнитной жидкости в кювете 159 см3, на фотографиях рис. 4, наблюдается, что на месте образования шеек-перетяжек, в окрестности боковых участков плоскости цилиндра левая и правая области магнитной жидкости в кювете соединяются, и в объеме магнитной жидкости формируются воздушные полости.
Эксперименты продемонстрировали, что при увеличении интенсивности наружного приложенного магнитного поля в окрестности боковых участков поверхности цилиндра воздушные полости возрождались в противоположном порядке. Появились конические выемки. Вслед за этим, по образующей цилиндра, вершина конических выемок спускалась вниз. Затем, на дне кюветы, возле нижнего торца цилиндра, на дне кюветы сформировался просвет полости. После этого, полость снова обретала вид усеченного конуса, уменьшающегося в направлении силы тяжести.
Осуществлялось численное сопоставление формы свободной поверхности магнитной жидкости, находящейся вокруг цилиндр, полученной в эксперименте и описываемой уравнением (6). Из эксперимента определялся радиус – вектор точки свободной поверхности магнитной жидкости в и нижнего торца цилиндра (z = 0,02 м) при значении угла J = 0 °. Найденное значение радиуса – вектора позволило определить параметр с из уравнения (6) определялся параметр с. Это значение величины с использовалось при построении границы раздела магнитная жидкость воздух для значений 0 < J < 90 °. Результаты представлены в таблице. Исходя из таблицы, можно увидеть, что различие экспериментальных и теоретических значений радиуса растет с увеличением угла J. Хотя это различие не превышает 8 %.
Значения радиус-векторов точек свободной поверхности магнитной жидкости, окружающей цилиндр во внешнем магнитном поле H0 = 105 кА/м, полученные экспериментально (rэкс) и по решению уравнения (6) (rтеор)
|
J |
rэкс * 10-3, м |
rтеор * 10-3, м |
Относительная погрешность, % |
|
0 |
22,1 |
22,1 |
0,0 |
|
5 |
21,7 |
21,9 |
0,9 |
|
10 |
21,7 |
21,5 |
0,9 |
|
15 |
20,1 |
20,8 |
3,4 |
|
20 |
19,1 |
19,9 |
4,0 |
|
25 |
17,9 |
18,6 |
3,8 |
|
30 |
16,6 |
17,2 |
3,5 |
|
35 |
15,4 |
15,5 |
0,6 |
|
40 |
14,3 |
13,8 |
3,6 |
|
45 |
13,1 |
12,2 |
7,4 |
Заключение
Найденное теоретически распределение магнитного поля, дает объяснение тому, что силами магнитного поля из полости цилиндра жидкость выталкивается. В полости цилиндра магнитное поле близко к нулю. Используемый в опыте цилиндр имел ограниченную длину, вблизи его торцов поле было неравным нулю. В неоднородном магнитном поле на магнитную жидкость действует сила, направленная в сторону большего поля. Магнитная жидкость из полости цилиндра и выталкивалась указанной силой.
Работа выполнялась при финансовой поддержки РФФИ (проект № 17-01-00037).
Библиографическая ссылка
Алексеева И.И., Симоновский А.Я. МАТЕМАТИЧЕСКОЕ И ЭКСПЕРИМЕНТАЛЬНОЕ МОДЕЛИРОВАНИЕ СВОБОДНОЙ ПОВЕРХНОСТИ МАГНИТНОЙ ЖИДКОСТИ В ОКРЕСТНОСТИ ПОЛОГО ЦИЛИНДРА // Научное обозрение. Педагогические науки. 2019. № 4-3. С. 25-29;URL: https://science-pedagogy.ru/ru/article/view?id=2112 (дата обращения: 11.03.2026).


 science-review.ru
science-review.ru