Научный журнал

Научное обозрение. Педагогические науки

ISSN 2500-3402

ПИ №ФС77-57475

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Губанова А.А. 1 Кустиков Д.А. 1

---

1 Донской государственный технический университет

Целью данной работы является повышение качества формируемой поверхности за счет установления стационарными траекториями при фрезеровании винтовыми фрезами. Статья посвящена динамике процесса попутного фрезерования боковыми режущими лезвиями концевых фрез, а конкретно, винтовым. В работе подробно рассмотрены принципы формирования распределенных силовых нагрузок для различных режимов резания винтовых фрез, получены модели деформаций траекторий фрезы в процессе резания, изложены алгоритмы и результаты численного анализа полученных моделей. Также в данной работе рассмотрен процесс попутного фрезерования винтовыми фрезами, который показывает все особенности нелинейной динамики. Рассмотрены принципы формирования распределенных силовых нагрузок для винтовых фрез, получены модели деформаций траекторий фрезы в процессе резания, изложены аналитический и на основе компьютерного моделирования анализы преобразования траекторий и установления стационарной траектории периодических движений инструмента относительно обрабатываемой детали. Предложен и показан способ, учитывающий представление сил, действующих на инструмент в координатах состояния системы. При этом учитываются влияние на силы изменения сформированной поверхности предыдущим зубом, нелинейная зависимость сил, формируемых в области контакта задней грани инструмента.

Статья в формате PDF

803 KB

фрезерование

винтовые фрезы

стационарное состояние

площадь срезаемого слоя

деформационные смещения

1. Заковоротный В.Л. Динамика процесса резания. Синергетический подход / В.Л. Заковоротный, М.Б. Флек. – Ростов н/Д: Терра, 2006. – 880 с.

2. Заковоротный В.Л., Фам Д.- Т., Нгуен С.- Т. Математическое моделирование и параметрическая идентификация динамических свойств подсистемы инструмента и заготовки // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Технические науки. – 2011. – № 2. – С. 38 – 46.

3. Gubanova A. Investigation of stationary trajectories with associated milling by spur gears // XIV International Scientific-Technical Conference «Dynamic of Technical Systems» (DTS-2018). Journal MATEC Web of Conferences. – 2018ю – Vol. 226. – https: //doi.org /10.1051/ matecconf/ 201822 0 DTS-2018 6 6 2004 (дата обращения 14.12.2018).

4. Zakovorotnyi V.L., Lukyanov A.D. Parametric phenomena in processing control in machine-tools // 6th International Scientific Conference «Applied Sciences and technologies in the United States and Europe: common challenges and scientific findings», 2014. – PP. 113–118.

5. Заковоротный В.Л., Губанова А.А., Христофорова В.В. Бифуркации стационарных многообразий, формируемых в окрестности равновесия в динамической системе резания // Вестник Донского государственного технического университета. – 2015. – Т. 15; № 1 (80). – С. 11–22.

Сложность изучения динамики процесса фрезерования заключается в том, что при математическом описании этого процесса приходится рассматривать нелинейные уравнения с периодически изменяющимися коэффициентами, которые обусловлены прерывистостью процесса резания каждым зубом фрезы [1]. В настоящее время огромный выбор фрез предполагает выбирать тип материала, в результате чего заготовке придается необходимая форма и она превращается в деталь самой разной формы. В данном случае рассматривается фрезерование винтовыми фрезами. Такие фрезы получили наибольшее распространение в промышленности, так как обработка сопровождается меньшими вариациями сил.

В этом случае фреза имеет лезвия, расположенные под некоторым углом θ по отношению к оси инструмента. В этом случае точка встречи вершины режущего лезвия с заготовкой смещается в зависимости от углов φ и θ. Здесь точка встречи остается неизменной по длине фрезы. Кроме этого длина контакта режущего лезвия с заготовкой изменяется в функции угла поворота фрезы. Таким образом, при врезании каждого зуба в заготовку длина поверхности резания монотонно возрастает. На выходе после обработки каждой строки поверхности заготовки длина контакта инструмента также монотонно уменьшается. Таким образом, при рассмотрении динамики фрезерования винтовыми фрезами процесс обработки можно интерпретировать как точение с переменным припуском и длиной контакта режущего лезвия [2]. Так как величина подачи на зуб более чем на порядок превышает длину контакта, то некоторым смещением при обработке каждой строки поверхности заготовки можно пренебречь.

Теперь проанализируем изменения сил и деформаций в процессе установления стационарного состояния. Для этого воспользуемся аппроксимациями площади срезаемого слоя в виде трапеции (рис. 1).

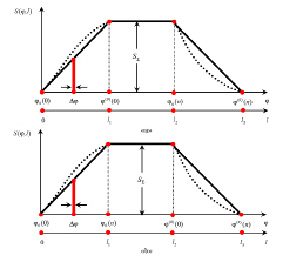
Рис. 1. Аппроксимация изменения площади срезаемого слоя в зависимости от угла поворота фрезы

Участки «φ₀(0), φ₀⁽⁰⁾⁽0)» и «φ₀(n), φ₀⁽⁰⁾ (n)» соответствуют врезанию и выходу инструмента. На участке «φ₀⁽⁰⁾ (n), φ₀(n)» мы имеем стационарное резание. Рассмотрим примеры изменения площади срезаемого слоя при фрезеровании и соответствующие им траектории сил в плоскости в предположении, что деформационные смещения инструмента отсутствуют.

Пусть исходной является кинематическая траектория. Для этого случая вычислим эволюционную траекторию установления стационарного состояния. Рассмотрим первый случай. Для определения параметров аппроксимирующей трапеции вариаций площади срезаемого слоя достаточно знать ее высоту S_∑ и углы φ₀(0), φ₀(n), φ₀⁽⁰⁾ (0), φ₀⁽⁰⁾ (n). Здесь главное значение имеет площадь, соответствующая стационарному состоянию. В этом случае сечением срезаемого слоя аппроксимируется треугольником. В данном случае основанием треугольника является установившееся значение линии контакта вершины зуба с обрабатываемой заготовкой (на рис. 2. это линия «2–3»). Для определения основания треугольника необходимо вычислить отрезок «1–4» на рис. 2. Он определяется на основе определения точки пересечения прямой

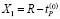
и окружности

.

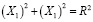Очевидно площадь

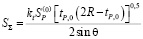, (1)

где R – радиус фрезы. Заметим, что все выполненные рассуждения относятся к случаю, когда 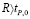Обычно 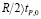. Выражение (1) удобно представить в следующем виде

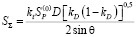, (2)

где D – диаметр фрезы; 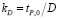. Вычисления показывают: выражение 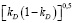при малых 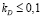можно аппроксимировать прямой. При этом точность аппроксимации возрастает при 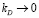. Например, при kD=0,05 погрешность линейной аппроксимации не превышает 2 %.

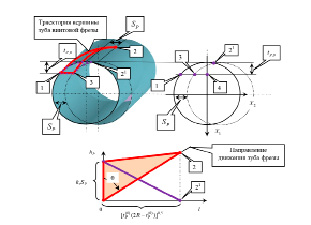
Рис. 2. Иллюстрация связи площади срезаемого слоя с технологическими режимами (область φi ∈(φ₀(0), φ₀⁽⁰⁾ (0)) )

Для точного вычисления необходимо воспользоваться приведенными ранее зависимостями. Однако при малых значениях kD точные значения длины контакта и вычисленные по зависимости (2) практически совпадают. В зависимость (1) входят технологические режимы. Поэтому при определении изменений сил и деформаций выражениями (2) пользоваться удобнее. Здесь рассматривается случай, когда перекрытия контакта отдельными зубьями нет. Поэтому после каждого акта взаимодействия силы, действующие на инструмент, обнуляются. Следовательно, величина технологического припуска и подачи на зуб остаются неизменными. Тогда неизменными остаются и углы встречи режущего лезвия с заготовкой. Для определения остальных базовых углов достаточно знать высоту трапеции. Анализу подлежит значение площади . Если в (2) воспользоваться линейной аппроксимацией влияния технологического припуска на площадь срезаемого слоя, то для определения модуля силы резания справедливо

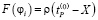, φ_i ∈(φ₀(0), φ₀⁽⁰⁾ (n)), (3)

где X – деформация инструмента в направлении угла φ₀(0); Значение

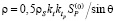
вытекает из [3] при определении изменений сил и деформаций при фрезеровании фрезами имеет смысл жесткости процесса резания; 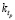– коэффициент линейной аппроксимации. Мы имеем полную аналогию со случаем фрезерования прямозубыми фрезами. Тогда деформационные смещения и силы определяем, как и ранее, последовательно после обработки поверхности первым, вторым и так далее зубьями. Для этого необходимо воспользоваться уравнением статического равновесия сил упругости и сил резания, то есть

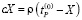. (4)

Поэтому для вычисления деформационных смещений из (4) можно воспользоваться ранее полученными выражениями (2) и (3). Однако, в отличие от ранее рассмотренного случая необходимо использовать угловые коэффициенты ориентации сил; зависимость справедлива для соотношений диаметра фрезы и технологического припуска 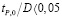[4]. В противном случае необходимо пользоваться непосредственно зависимостью (1).

Рассмотрим характерные примеры изменения сил и деформаций в процессе установления стационарного состояния (рис. 3 – 7). Параметры процесса: жесткость резания ρ=200 кг/мм, жесткость инструмента с=400 кг/мм, глубина tP,0 = 10 мм, величина подачи на зуб 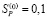мм, скорость резания – 80,0 м/мин, ширина фрезеруемой поверхности H0=5,0 мм, угол наклона зуба фрезы – 35°, угловые коэффициенты – χ _1,Э =0,722, χ_2,Э = 0,691. Переходные процессы при установлении стационарного режима принципиально зависят от соотношения жесткости процесса резания и жесткости инструмента. Поэтому приведем также кривые для других соотношений (ρ=600 кг/мм, с=200 кг/мм). Данные, аналогичные рис. 3 – 5, приведены на рис. 6, 7. Здесь наблюдаются существенные вариации сил и деформационных смещений. Их можно уменьшить в случае, если уменьшить угол наклона зуба.

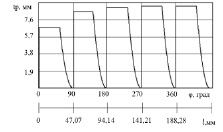
Рис. 3. Изменение глубины резания в зависимости от угла поворота фрезы и пути резания

Рис. 4. Изменение сил по мере становления стационарной траектории

Рис. 5. Изменение деформационных смещений инструмента в плоскости по мере становления стационарной траектории

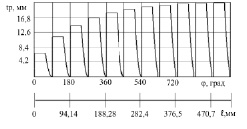
Рис. 6. Изменение глубины резания в зависимости от угла поворота фрезы и пути резания

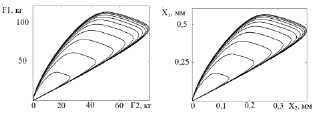
Рис. 7. Изменение сил «а» и деформационных смещений «b» инструмента в плоскости по мере становления стационарной траектории

При фрезеровании в установившемся состоянии, в отличие, например, от точения, существуют периодические упругие деформационные смещения инструмента относительно заготовки вдоль траектории обработки. Вместо точки равновесия рассматривается некоторая замкнутая траектория упругих деформаций [5]. Это траектория, к которой асимптотически приближаются все траектории, при этом перераспределяются силы и деформации, взаимно влияющие друг на друга через механизм изменения площади срезаемого слоя.

Библиографическая ссылка