На протяжении многих десятилетий ученые и инженеры используют новые технологии трехмерного (3D) зондирования и визуализации реальных объектов. В отличие от традиционных методов двумерной (2D) визуализации, технологии 3D-визуализации могут существенно захватывать 3D-структуру, диапазон и текстурную информацию объектов. Существует множество технологий 3D-визуализации, таких как голография и связанные с ней методы интерферометрии, стереоскопия, методы подсветки рисунков и методы времени полета.
Мультиперспективная 3D-визуализация получатся когда в 3D-сцены встраивают обычные 2D некогерентные изображения нескольких ракурсов, для формирования которых может быть использован один недорогой фотоаппарат.
В 1908 году Липпман [1] предложил новую технику, названную интегральной съемкой (ИС), формирования истинного 3D-изображения, которое можно наблюдать с параллаксом и квази-непрерывными углами обзора. Этот метод, который основан на принципе обратимости световых лучей, производит автостереоскопические изображения. При этом для восприятия 3D-изображений не требуется никаких специальных устройств просмотра. Помимо раннего наблюдения за ИС Липпмана [1], на протяжении большей части 20–го века не было никакой существенной деятельности в этой области. Это получилось в основном из-за отсутствия отработанных технологий для экономически эффективных устройств такого высокого разрешения как дисплеи и микролинзовые матрицы.
Тем не менее, благодаря прогрессу в области оптико-электронных датчиков, таких как КMOП и ПЗС, а также устройств отображения, таких как ЖК-дисплеи, принципы ИС в настоящее время получили дальнейшее развитие. В своей нынешней форме ИС относится к более широкому классу многозональных систем визуализации и стала перспективным подходом к 3D-зондированию и визуализации. Методы ИС были развиты для восприятия, захвата и визуализации 3D-изображений с использованием современных оптических и цифровых приборов обработки изображений [2]. Положительные результаты исследований были достигнуты в том числе для 3D-дисплеев в телевидении [3], для автоматического распознавания целей [4], для разделения объектов по цвету [5], для формирования 3D-подводного изображения [6], для медицинской визуализации [7] и другие [8].
Профилометрическая 3D-реконструкция. При получении плоских 2D-изображений может быть восстановлен трехмерный профиль зарегистрированной сцены. Для этого может быть использована спектральная картина излучения (Spectral picture of a radiation – SRP) для захвата интенсивности излучения определенной длины волны, которая определяет цвет объектов в направлении нахождения поверхности объектов. В [5, 9] описан метод вывода глубины Ламбертовых поверхностей из статистики SRP в многоцветовой системе визуализации с использованием цветовой фильтрации отдельных объектов. Излучателем Ламберта в физике называют диффузно-излучающую поверхность, которая характеризуется диаграммой направленности рассеянного излучения, имеющая форму окружности с максимумом перпендикулярным к поверхности объекта.
Для каждой точки в трехмерном пространстве (x;y;z), SRP, L (θ;φ;λ), описывает интенсивность излучения в зависимости от направления (θ;φ) и длины волны (λ). На практике каждый пиксель изображения обеспечивает заданный цвет из SRP вдоль связанного главного луча. Для упрощения рассматривается интегральная схема визуализации, в которой датчики изображения расположены на плоскости K×L сетки. Лучевая диаграмма между двумя точками в пространстве и соответствующие изображения в интегральной системе изображений проиллюстрированы на рис. 1.
Для наглядности показана только система координат плоскости Y-Z. Для точек поверхности объекта p(o) x(o); y(o); z(o), K×L интенсивности выборки этой точки собираются датчиками изображения K×L с неидентичных точек (разные SRP). Однако, интенсивность (λ) среди этих SRP должны быть соотнесены друг с другом, если эта точка удовлетворяет предположению Ламберта. Если точка, P(v) (x(v); y(v); z(v)) , находится в свободном пространстве, то есть не принадлежит ни к одной поверхности объекта в 3D-пространстве, то K×L интенсивности собранных выборок, скорее всего, будут отличаться, поскольку эти выборки, вероятно, из разных частей анализируемого изображения.
Это изменение интенсивности среди собранных SRP может быть использовано для оценки глубины точек объекта с помощью следующей формулы:
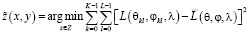 , (1)
, (1)
где L – среднее значение SRP по всем направлениям и Z – диапазон объектов, представляющих интерес.
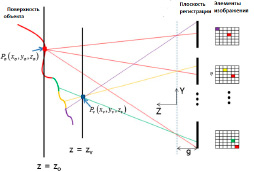
Рис. 1. Лучевая диаграмма между двумя точками в пространстве
Уравнение (1) можно объяснить как дисперсию. Функция SRP достигнет локального минимума на реальной глубине точек объекта. Как только глубина точек объекта восстанавливается, можно реконструировать 3D-профиль сцены.
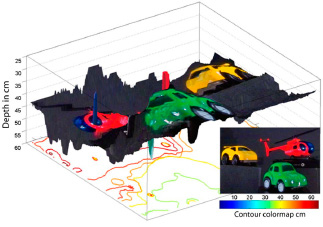
Рис. 2. 3D-визуализация по цвету
Интегральная визуализация может использоваться также для трехмерной визуализации подводных объектов. Подводная съемка по своей сути отличается от аэрофотосъемки из-за поглощения и рассеяния света от различных подводных частицы и молекул воды. Метод интегральной визуализация учитывает пространственное положение объектов из-за разницы в показателе преломления воды.
Подсчет фотонов и 3D-визуализация. Подсчитывать фотоны в объединенном 2D-изображении было предложено для выполнения 3D-визуализации [10] и 3D распознавания целей [8] в условиях низких уровней освещенности сцены. При этом каждый объект имеет различную яркость и, как следствие, различный поток фотонов в зависимости от дальности до объекта. 3D-визуализация при этих условиях может быть выполнена с использованием алгоритма вычислительной реконструкции, основанного на оценке максимального правдоподобия [10] потока фотонов. Плотность вероятности потока фотонов задается функцией вероятности Пуассона [7]:
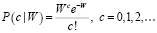 (2)
(2)
где c – число наблюдаемых фотонов, а W – интегральная интенсивность за определенный период времени и постоянная. Фактически, параметр Пуассона W для количества фотонов в каждом пикселе изображения пропорционален интенсивности излучения пикселя изображения [8]. На основе алгоритма MAP-EM [9] восстановленную интенсивность объекта r можно получить по следующему итерационному уравнению:
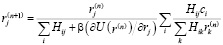 , (3)
, (3)
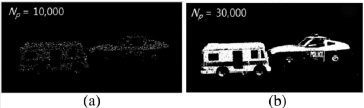
Рис. 3. Метод подсчета фотонов для 3D-визуализации
где H(ij) построен дискретной функцией распространения точки объектива изображения приемистости, U(r) является функционалом предшествующей энергии (например, ограничение полной вариации, β – параметр регуляризации, n – время итерации, а i, j, k – индексы пикселей. Итерация останавливается, когда среднеквадратичная ошибка между r(n+1) и r(n) меньше заданного порога. На рис. 3 показаны две группы результатов подсчета фотонов c разным числом посчитанных фотонов N(p).
Ограничение полной вариации является эффективным для восстановления интегральных изображений, полученных с помощью фотонных счетных датчиков [11]. В [12] также было продемонстрировано, что он эффективен для восстановления мало-фотонных интегральных изображений, полученных с помощью обычных ПЗС- или КМОП-датчиков. Когда использованы обычные датчики, изображение типично повреждено шумом восходящего потока теплого воздуха и отсчетами шума Пуассона, источником которого является случайный процесс появления фотона. Но, используя алгоритм полного вариационного ожидания максимального правдоподобия формируется четкое изображение несмотря на то, что исходное изображение имеет отношение сигнал-шум намного ниже 1. В [12] реальные экспериментальные результаты показали успешную реконструкцию интегральных изображений, полученных обычной камерой, освещенной в среднем четырьмя фотонами на пиксель.
Библиографическая ссылка
Прохновский М.А., Сальников И.И. ИНТЕГРАЛЬНАЯ ВИЗУАЛИЗАЦИЯ ПРИ ФОРМИРОВАНИИ ОБЪЕМНЫХ ТРЕХМЕРНЫХ ИЗОБРАЖЕНИЙ // Научное обозрение. Педагогические науки. 2019. № 3-2. С. 75-78;URL: https://science-pedagogy.ru/ru/article/view?id=1960 (дата обращения: 30.12.2025).


 science-review.ru
science-review.ru