Искусственные нейронные сети – это одно из направлений исследований в области искусственного интеллекта, основанное на попытках воспроизвести техническими средствами свойства нервной системы человека.
Нейрон Маккаллока–Питтса был ранней моделью функционирования мозга. Эта линейная модель могла распознавать две категории выходов, проверяя, является значение f(x, w) положительным или отрицательным. Конечно, чтобы модель соответствовала желаемому определению категорий, нужно было правильно подобрать веса. Веса задавал человек. В 1950-е годы был изобретен перцептрон – первая модель, которая могла в процессе обучения находить веса, определяющие категории, имея примеры входных данных из каждой категории. Модель адаптивного линейного элемента, относящаяся примерно к тому же времени, просто возвращала само значение f(x) для предсказания вещественного числа и также могла обучаться предсказанию чисел на данных [1].
Искусственный нейрон является структурной единицей искусственной нейронной сети и представляет собой аналог биологического нейрона.
С математической точки зрения искусственный нейрон – это сумматор всех входящих сигналов, применяющий к полученной взвешенной сумме некоторую простую, в общем случае, нелинейную функцию, непрерывную на всей области определения [2] (рис. 1). Обычно, данная функция монотонно возрастает. Полученный результат посылается на единственный выход.
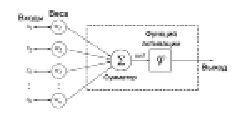
Рис. 1. Математический нейрон
Искусственные нейроны объединяются между собой определенным образом, образуя искусственную нейронную сеть. Каждый нейрон характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены. Он обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона, с которой сигнал поступает на синапсы следующих нейронов.
Каждый синапс характеризуется величиной синаптической связи или ее весом wi, который является эквивалентом электрической проводимости биологических нейронов [3].
Текущее состояние нейрона определяется, как взвешенная сумма (net) его входов xi.
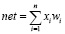
Просто так подавать взвешенную сумму на выход достаточно бессмысленно. Нейрон должен как-то обработать ее и сформировать адекватный выходной сигнал. Именно для этих целей и используют функцию активации.
Она преобразует взвешенную сумму в число, которое и является выходом нейрона (выход нейрона обозначим переменной out).
Для разных типов искусственных нейронов используют самые разные функции активации. В общем случае их обозначают символом ?(net). Указание взвешенного сигнала в скобках означает, что функция активации принимает взвешенную сумму как параметр [3].
Активационная функция (Activation function) (?(net)) – функция, принимающая взвешенную сумму как аргумент. Значение этой функции и является выходом нейрона (out).
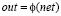 .
.
Самыми известными функциями активации являются:
– функция единичного скачка;
– семейство сигмоидальных или логистических функций;
– гиперболический тангенс.
Самый простой вид функции активации. Выход нейрона может быть равен только 0 или 1. Если взвешенная сумма больше определенного порога b, то выход нейрона равен 1. Если ниже, то 0.
Запишем эту функцию активации математически:
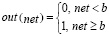 .
.
Выход нейрона (out) зависит от взвешенной суммы (net) следующим образом: если net меньше порога (b), то out равен 0. А если net больше или равен порогу b, то out равен 1.
Графически эту функцию активации можно изобразить следующим образом (рис. 2).
На горизонтальной оси расположены величины взвешенной суммы. На вертикальной оси – значения выходного сигнала. Как легко видеть, возможны только два значения выходного сигнала: 0 или 1. Причем 0 будет выдаваться всегда от минус бесконечности и вплоть до некоторого значения взвешенной суммы, называемого порогом. Если взвешенная сумма равна порогу или больше него, то функция выдает 1.
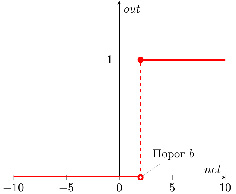
Рис. 2. Функция единичного скачка
Существует целое семейство сигмоидальных функций, некоторые из которых применяют в качестве функции активации в искусственных нейронах [4]. Все эти функции обладают некоторыми очень полезными свойствами, ради которых их и применяют в нейронных сетях. Самая часто используемая в нейронных сетях сигмоида – логистическая функция (рис. 3).
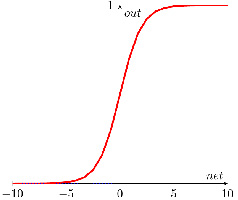
Рис. 3. Логистическая функция
График этой функции представляет некоторое подобие латинской буквы S, откуда и пошло название семейства этих функций.
Математически активационная функция описывается:
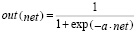 .
.
Параметр a – это число, которое характеризует степень крутизны функции. На рис. 4 представлены логистические функции с разными значениями a.
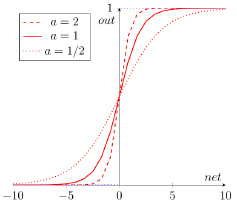
Рис. 4. Логистическая функция с разными значениями параметра a
Значение, получаемое при использование логистической функции с разными значениями параметра a в качестве функции активации, будет между 0 и 1. Причем чем больше взвешенная сумма, тем ближе выход будет к 1 (но никогда не будет точно ей равен). И наоборот, чем меньше взвешенная сумма, тем ближе выход нейрона будет к 0.
Свойства логистической функции:
– она является «сжимающей» функцией, то есть вне зависимости от аргумента (взвешенной суммы), выходной сигнал всегда будет в пределах от 0 до 1;
– она более гибкая, чем функция единичного скачка – ее результатом может быть не только 0 и 1, но и любое число между ними;
– во всех точках она имеет производную, и эта производная может быть выражена через эту же функцию.
Именно из-за этих свойств логистическая функция чаще всего используются в качестве функции активации в искусственных нейронах.
Есть еще одна сигмоида – гиперболический тангенс изображена на рисунке 5. Он применяется в качестве функции активации биологами для более реалистичной модели нервной клетки [5].
Такая функция позволяет получить на выходе значения разных знаков (например, от –1 до 1), что может быть полезным для ряда сетей.
Функция записывается следующим образом:
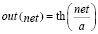 .
.
Параметр a также определяет степень крутизны графика этой функции.
Гиперболический тангенс обладает всеми полезными свойствами, которые имеет и логистическая функция.
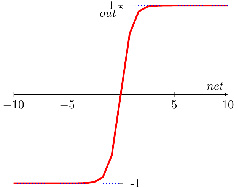
Рис. 5. Гиперболический тангенс
Математическая модель искусственного нейрона с n входами:
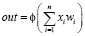 ,
,
где ? – функция активации, взвешенная сумма, как сумма n произведений входных сигналов на соответствующие веса:
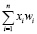 .
.
Перспективы развития искусственных нейронных сетей обусловлены тем, что даже на существующем уровне внутренней организации искусственные нейронные сети способны справляться с рядом задач, считавшихся до последнего времени трудными или вообще не поддающимися решению при помощи компьютеров традиционной архитектуры.
Библиографическая ссылка
Малышев А.Н., Данилов Е.А. ОБЗОР НЕКОТОРЫХ АКТИВАЦИОННЫХ ФУНКЦИИ МАТЕМАТИЧЕСКОГО НЕЙРОНА // Научное обозрение. Педагогические науки. 2019. № 3-2. С. 39-43;URL: https://science-pedagogy.ru/ru/article/view?id=1952 (дата обращения: 19.12.2025).


 science-review.ru
science-review.ru