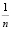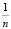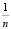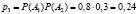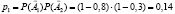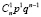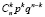Научный журнал

Научное обозрение. Педагогические науки

ISSN 2500-3402

ПИ №ФС77-57475

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Нахман А.Д. 1

---

1 ФГБОУ ВО «Тамбовский государственный технический университет»

Содержание стохастической подготовки в школьном курсе математики ограничивается кругом вопросов, связанных с вычислением вероятностей случайных событий и обработкой результатов выборок. Целесообразность рассмотрения случайных величин обусловлена рядом обстоятельств: каждое случайное событие ассоциировано с подходящей случайной величиной, а эмпирические распределения являются «случайными срезами» теоретического распределения некоторого количественного признака генеральной совокупности. В работе сконструировано содержание модуля «Случайные величины» (профильный уровень математики в старшей школе). Предлагается система технологических приемов его изучения. Обоснована целесообразность включения данного модуля в систему «звеньев» стохастической линии. Установлено, что указанный содержательный компонент обладает признаками инновационности. Обсуждаются наиболее значимые понятия и факты, проанализированы соответствующие аналогии и различия в случаях дискретных и непрерывных распределений. Основные результаты состоят в следующем. Выстроен пошаговый алгоритм анализа распределений дискретных случайных величин. Алгоритм исследования распределений непрерывных случайных величин адаптирован к школьному курсу, что позволило избежать использования инструментария несобственных интегралов. Введены распределения специальных величин как «ассоциированных» случайных величин в знакомых учащемуся стандартных вероятностных схемах. Предложен приём изучения элементов математической статистики на основе идеи связи эмпирических и теоретических распределений случайных величин.

Статья в формате PDF

0 KB

математическое образование

случайные величины

анализ распределений

эмпирические распределения

1. Концепция развития российского математического образования [Электронный ресурс]. – Режим доступа: www.math.ru/conc/vers/conc-3003.html (дата обращения: 02.02.2018).

2. Нахман А.Д. Стохастическая линия как инновационная содержательно-методическая линия в курсе математики /А.Д. Нахман // Актуальные инновационные исследования: наука и практика. – 2009. – № 3. – 11 с.

3. Терехова Л.А. Элементы стохастики как средство усиления внутрипредметных связей школьного курса математики / Л.А. Терехова // Вестник Тамбовского университета. Серия: Гуманитарные науки. – 2008. – № 5. – С. 347–350.

4. Нахман А.Д. Введение в стохастическое моделирование: учебное пособие / А.Д. Нахман, Ю.В. Родионов. – Электрон. текстовые данные. – Саратов: Ай Пи Эр Медиа, 2018. – 89 c. – Режим доступа: http://www.iprbookshop.ru/70761.html (дата обращения: 02.02.2018).

5. Мордкович А.Г. Математика: алгебра и начала анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных организаций (базовый и углубленный уровни) / А.Г. Мордкович, П.В. Семёнов. – М.: Мнемозина, 2014. – 311 с.

6. Рябушко А.П. Индивидуальные задания по высшей математике / А.П. Рябушко, В.В. Бархатов и др. – Минск: Изд-во «Вышэйшая школа», 2013. – Ч. 4. – 336 с.

В условиях реализации ФГОС нового поколения и Концепции развития российского математического образования [1] актуализируется задача обновления содержания курса математики. Важной его инновационной составляющей является стохастическая линия. В перечне требований ФГОС к предметным результатам освоения основных образовательных программ предусмотрена «сформированность представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире,… умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин». Однако в настоящее время соответствующее содержание школьного курса ограничивается кругом вопросов, связанных с вычислением вероятностей случайных событий и обработкой результатов выборки. Вместе с тем каждое случайное событие ассоциировано с подходящей случайной величиной (см. п. 1 настоящей работы), а эмпирические распределения являются «случайными срезами» теоретического распределения некоторого количественного признака Х генеральной совокупности и служат, в некотором смысле, средством получения информации об Х. Следовательно, стохастический материал (в рамках его изучения на профильном уровне) целесообразно пополнить модулем «Случайные величины». Данный модуль может быть отнесен к компонентам инновационного содержания курса математики [2], поскольку:

– рассмотрение случайной величины как измеримой функции на некотором вероятностном пространстве соответствует современному уровню развития метрической теории функций;

– изучение случайных величин, возникающих в решении ряда прикладных и практических задач, способствует реализации значительного прикладного потенциала курса математики и укреплению его внутрипредметных связей [3];

– случайные величины служат средством моделирования недетерминированных систем [4], в силу чего овладение соответствующими понятиями и фактами направлено на формирование способностей принятия оптимальных решений в ситуациях неопределенности.

1. Случайные величины: понятийный аппарат

1.1. Многие случайные события связаны с наблюдением заранее непредсказуемых значений некоторых числовых величин: например, число очков, выпавших на грани игрального кубика, номинал монеты, случайным образом извлекаемой из кошелька, масса выбираемого на рынке арбуза и др.

Более того, любое случайное событие А можно связать со случайной же числовой величиной η, если ввести понятие индикатора события: случайная величина η = η(А), по определению, принимает значение, равное 1, если А наступает, и значение, равное 0, если А не наступает.

1.2. Изложение начальных понятий и фактов, связанных со случайными величинами, по нашему мнению, следует начать с соответствующих примеров, часть из которых могут привести сами учащиеся. Далее выделяются следующие признаки случайной величины Х:

– Х – это числовая величина;

– в каждом опыте она принимает одно и только одно значение;

– это значение заранее неизвестно и зависит от случайных причин.

На следующем этапе случайные величины классифицируются по признакам их дискретности и непрерывности; соответствующие признаки и возможные примеры приведены в табл. 1.

1.3. Одним основных вопросов, связанных со случайными величинами, является вопрос: какова вероятность, что в проводимом эксперименте величина Х примет заданное значение x0? Однако этот вопрос в случае непрерывной случайной величины практически всегда имеет тривиальный ответ: такая вероятность равна нулю. В самом деле, такие события, как покупка яблока весом ровно 111,243 грамма, загрузка файла в течение заранее запланированных 3 мин и 24,4 секунды и т.п., учащиеся охарактеризуют как практически невозможные. В случае непрерывных случайных величин более естественна следующая постановка вопроса: какова вероятность, что в проводимом эксперименте значение Х окажется в заданном числовом интервале (вес случайно выбранного яблока будет от 110 до 120 граммов, загрузка файла произойдет в течение времени, не превышающего 4 мин и т.д.).

2. Анализ распределений дискретных случайных величин

Опорными понятиями и фактами для изучения таких распределений служат: понятие событий попарно несовместных и образующих полную группу, понятие суммы событий, формула вероятности суммы попарно несовместных событий. Для построения законов конкретных распределений учащийся должен владеть умениями вычислять вероятность непосредственно по определению классической вероятности и с помощью стандартных формул (вероятность суммы, произведения, формула Бернулли).

Работа по анализу распределения ДСВ может быть организована следующим образом (примеры приведены ниже).

2.1. Построение закона распределения, т.е. соответствия между возможными значениями ДСВ и вероятностями этих значений. Пошаговый алгоритм здесь таков:

2.1.1. Выписать все возможные значения {xi} в порядке их возрастания (ранжировать значения).

2.1.2. Вычислить вероятность каждого возможного значения .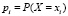

2.1.3. Представить закон распределения в виде ряда распределения, т.е. таблицы вида

(в этой таблице может быть как конечное, так и бесконечное число столбцов); при этом полезна и графическая интерпретация закона в виде многоугольника распределения – ломаной на координатной плоскости с вершинами (xi, pi).

Следует обратить внимание учащихся на то обстоятельство, что сумма вероятностей во второй строке ряда распределения с конечным числом п столбцов должна быть равна единице.

2.2. Тренинг в нахождении вероятностей событий вида X < χ, X ≤ χ, X > χ, X ≥ χ, где χ – любое заданное действительное число. Так, например, событие X < < (при χ > x1) равносильно наступлению ровно одного из попарно несовместных событий , где xl – наибольшее из тех ранжированных значений, которое меньше χ. Следовательно, по формуле сложения вероятностей попарно несовместных событий, 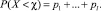Следует заметить, что события вида X < χ и X ≥ χ являются противоположными, а значит, 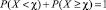, так что одно из слагаемых может быть легко найдено, если известно другое.

2.3. Вычисление математического ожидания M(X), формула для которого (в случае конечного перечня значений ДСВ) имеет вид

M(X) = 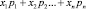. (2.1)

«Пропедевтическим шагом» к понятию математического ожидания может служить следующее теоретическое упражнение.

Случайная величина Х принимает с равной вероятностью любое из п различных значений 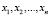(равномерно распределённая случайная величина). Построить ряд распределения этой ДСВ. Найти среднее арифметическое ее значений.

Решение состоит в реализации вышеприведенного алгоритма.

1) Возможные значения Х: .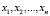

2) Согласно условию задачи

,

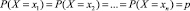где p – число, подлежащее нахождению; при этом сумма вероятностей

, или 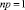, откуда .

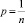3) Следовательно, ряд распределения данной ДСВ имеет вид

Искомое среднее арифметическое всех значений есть число

,

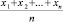которое можно также записать в виде

,

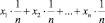т.е. в виде суммы произведений значений ДСВ на их вероятности.

Теперь можно перейти к рассмотрению математического ожидания (2.1) в общем случае: для произвольного распределения ДСВ сумма произведений всех значений ДСВ на их вероятности есть вероятностный аналог обычного среднего арифметического значений xi; в (2.1) учитывается «вероятностный вклад» каждого такого значения в получаемое «среднее».

2.4. Нахождение числовых характеристик рассеяния. Наряду с математическим ожиданием ДСВ полезно знать, насколько рассеяны ее значения относительно M(X). На первый взгляд, следовало бы найти среднее всех уклонений (разностей) xi – M(X), т.е. сумму произведений

,

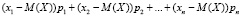однако эта сумма, будучи преобразована к виду

,

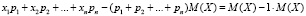оказывается равной нулю для любых распределений и, значит, не может служить характеристикой рассеяния конкретных распределений. Стоит выяснить причину такого явления: нулевое значение получилось за счет «интерференции» положительных и отрицательных уклонений xi – M(X). Чтобы устранить данную интерференцию, вводится в рассмотрение сумма произведений квадратов уклонений (xk – M(X))2 на вероятности pk соответствующих xk:

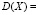
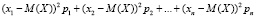; (2.2)

сумма (2.2) называется дисперсией распределения.

Более удобной для вычисления является формула

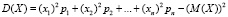, (2.3)

т.е. D(X) вычисляют как среднее квадратов значений без квадрата математического ожидания. Доказательство (2.3) и правило нахождения дисперсии равномерно распределенной дискретной случайной величины (дисперсия равна среднему квадратов значений величины минус квадрат среднего значения) могут быть предложены учащимся в качестве самостоятельно выполняемых теоретических упражнений.

Далее, полезно ввести среднее квадратическое отклонение значений Х от их среднего 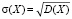, целесообразность которой объясняется тем, что σ(X) имеет размерность значений самой случайной величины (тогда как D(X) имеет размерность квадратов значений случайной величины).

2.5. Пример 1. На пути автомобиля два светофора. Светофор на пересечении с главной дорогой может его остановить с вероятностью 0,8, а светофор на пересечении со второстепенной дорогой остановит его с вероятностью 0,3. Составить ряд распределения случайной величины Х – числа остановок автомобиля перед светофорами. Каково наиболее вероятное число остановок автомобиля? Какова вероятность, что количество остановок на светофорах не превзойдет этого числа? Найти математическое ожидание, дисперсию и среднее квадратическое отклонение величины Х.

Решение.

1) Ряд распределения. Управление этой частью решения может быть выстроено следующим образом (табл. 2).

Таблица 2

Построение ряда распределения

Итак, получен следующий ряд распределения случайной величины Х:

2) Наиболее вероятное число остановок равно 1 (значение x2 = 1 имеет наибольшую из всех вероятностей p2 = 0,62).

Событие, состоящее в том, что число остановок не превзойдет 1, равносильно наступлению хотя бы одного из двух несовместных событий X = 0, X = 1. Следовательно, по формуле сложения вероятностей

.

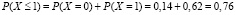Для нахождения математического ожидания, дисперсии и среднего квадратического отклонения записываем соответствующие формулы и проводим вычисления:

.

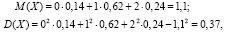
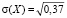
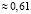Заметим, что среднее значение (среднее число остановок) M(X) ≈ 1 и наиболее вероятное значение x2 = 1 в данной задаче совпали.

К стандартным задачам по теме «Дискретные случайные величины» относятся также задачи на восстановление ряда распределения по известным числовым характеристикам.

Пример 2. Ряд распределения случайной величины Х имеет вид

Найти значения x1, x2 и p2, если даны математическое ожидание M(X) = 2,7, дисперсия D(X) = 0,21 и известно, что x1 < x2.

Проанализировав свойства вероятностей в ряде распределения и формулы для математического ожидания и дисперсии, учащиеся должны прийти к модели задания в виде системы алгебраических уравнений

;

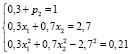здесь получаются две пары возможных решений x1 = 2, x2 = 3 и 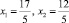. Согласно условию задачи x1 < x2, а тогда x1 = 2, x2 = 3.

3. Функция распределения. Распределение непрерывных случайных величин

Полноценное изучение распределений непрерывных случайных величин (НСВ) опирается на достаточно глубокое знание таких понятий анализа, как кусочная дифференцируемость, интегралы с переменным верхним пределом, несобственные интегралы и др. [5, 6]. Поэтому в школьном курсе возможен лишь ознакомительный уровень изучения и нестрогое обоснование ряда положений. Так, целесообразно основное внимание уделить распределениям НСВ на конечных отрезках; такие отрезки мы будем называть носителями распределения. Предлагаемые здесь технологические приёмы дают возможность избежать использования как несобственных интегралов, так и стандартного аппарата интегралов с переменным верхним пределом, применяемого для восстановления функции распределения по известной его плотности. Учащийся должен владеть понятиями непрерывности функции, производной и первообразной, уметь исследовать функцию на монотонность с помощью производной, использовать формулу Ньютона – Лейбница для вычисления интегралов.

3.1. «Отправной точкой» может служить задача о нахождении вероятности принятия НСВ значений в данном промежутке (a, b). Ввиду приведенных выше рассуждений интуитивного характера вероятности принятия НСВ значений X = a и X = b обе равны нулю, а тогда из геометрических соображений вытекает, что 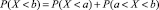; отсюда

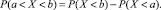(3.1)

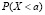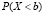Числа и являются значениями функции

F(x) = P(X < x). (3.2)

Функцию, определенную в виде (3.2), можно рассматривать теперь для любой случайной величины Х; она соотносит каждому 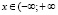) вероятность события, состоящая в принятии величиной X значения левее точки х. Вводится термин: функция распределения или интегральная функция распределения величины Х.

3.2. Обычно непрерывные случайные величины рассматривают при условии, что интегральная функция (3.2) непрерывна на всей числовой оси; естественно ожидать, что для ДСВ эта функция обладает разрывами.

На примере 1 п. 2.5 можно продемонстрировать, как строится функция распределения дискретной величины. Поскольку точки x1 = 0, x2 = 1, x3 = 2 разбивают числовую ось на три интервала, то функцию F(x) рассматриваем в каждом из этих интервалов. Левее точки x1 = 0 значений ДСВ нет, поэтому при x ≤ x1 событие X < x невозможно, а значит, F(x) = 0. Если 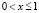, то левее точки x расположено единственное значение x1 = 0, поэтому 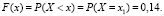При 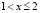событие X < x равносильно наступлению хотя бы одного из двух несовместных событий X = 0, X = 1. Следовательно, 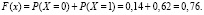Наконец, при x > 2 событие X < x достоверно, а значит, F(x) = 1. Итак,

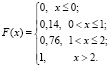
Получена кусочно-постоянная функция, обладающая разрывами (первого рода) в точках, определяемых возможными значениями ДСВ. Принцип ее построения естественно назвать принципом накопления вероятностей. В качестве теоретического упражнения на применение этого принципа можно предложить учащимся построить функцию распределения в общем случае ДСВ с конечным числом значений.

3.3. Полезно выделить свойства функции F(x) произвольной случайной величины Х, распределенной на конечном отрезке [a, b]:

1) 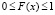при всех значениях х;

2) F(x) = 0 при 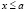и F(x) = 1 при x > b; в частном случае распределения НСВ соотношение F(x) = 1 имеет место и при x ≥ b;

3) F(x) является неубывающей функцией на отрезке [a, b].

Эти свойства продемонстрированы на примере п. 3.2; их доказательство в общем случае может быть предложено учащимся в следующем виде.

Свойство 1) очевидным образом вытекает из определения (3.2). Далее, при x ≤ a событие X < x является невозможным, а при x > b – достоверным, откуда и вытекает свойство 2). Для случая НСВ, ввиду непрерывности функции F(x), значение F(b) должно «непрерывно состыковаться» со значением F(x) = 1 для x > b, так что F(b) = 1.

Наконец, свойство неубывания функции F(x) для ДСВ вытекает из принципа накопления вероятностей. Для непрерывных же случайных величин из равенства (3.1) следует, что

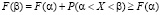при ,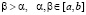

чем и доказано свойство 3).

Поскольку НСВ принимает каждое конкретное значение с нулевой вероятностью, то

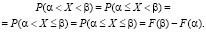
Пример. При каком значении параметра λ

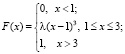
является функцией распределения некоторой непрерывной случайной величины?

Решение основано на свойстве 2: значение функции 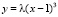в точке x = 3 должно совпасть со значением у = 1: 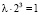, откуда 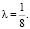Решение полезно также проиллюстрировать построением графиков: из семейства кубических парабол 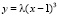надо выбрать такую, которая «непрерывно состыкуется» в точке x = 3 с прямой у = 1.

4. Плотность распределения непрерывной случайной величины

4.1. Если носителем распределения непрерывной случайной величины Х является отрезок [a, b] и F(x) – ее функция распределения, обладающая непрерывной производной на [a, b], то плотность распределения (плотность вероятности, дифференциальная функция) вводится в виде

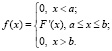(4.1)

Использование термина «плотность» оправдано следующими соображениями. По определению производной

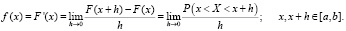(4.2)

Отношение, записанное под знаком предела, при h > 0 было бы естественно назвать средней плотностью вероятности принятия величиною Х значений на промежутке 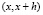, а тогда само значение предела (4.2) – плотностью вероятности в точке х.

4.2. В школьном курсе могут быть рассмотрены следующие свойства плотности распределения:

а) 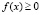для всех х;

б) 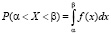для любых α и β, α < β;

в) 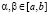(свойство нормированности).

В приведенных соотношениях легко усмотреть аналогию со свойствами вероятностей распределения ДСВ: суммированию вероятностей значений ДСВ здесь соответствует интегрирование f(x).

Доказательства свойств могут быть адаптированы к школьному курсу следующим образом:

а) Плотность f(x) неотрицательна как производная неубывающей функции F(x).

Свойство б) установим для 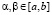(общий случай требует использования свойства аддитивности интеграла). Поскольку F(x) является одной из первообразных для f(x), то применима формула Ньютона – Лейбница в следующем виде:

= = ;

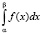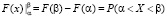в) Согласно свойству 2) п. 3.3 имеем

= ,

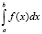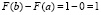что и утверждалось.

Пример. Плотность распределения некоторой НСВ задана в виде

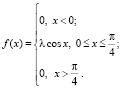
Найти значение параметра λ, вероятность 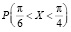и функцию распределения F(x).

При решении определяется носитель распределения – отрезок 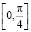. Средством нахождения неизвестного параметра λ может служить нормированность плотности (свойство б)), благодаря которому приходим к уравнению относительно искомого параметра и получаем λ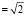. Итак, 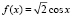при 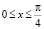. Далее, 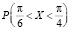= 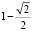согласно б).

Наконец, функция распределения F(x) будет равна нулю левее носителя распределения 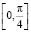и равна единице правее носителя. На самом же отрезке 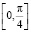функция F(x) является первообразной (см. (4.1)) для 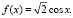Следовательно, 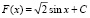, где значение постоянной C можно найти из соотношения F(0) = 0 (или из равенства 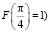: , откуда C = 0. Итак,

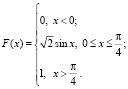
Заметим, что решение подобных заданий способствует закреплению навыков интегрирования.

5. Числовые характеристики непрерывных случайных величин

5.1. В качестве числовых характеристик непрерывной случайной величины Х, распределенной на отрезке [a, b] с плотностью f(x) рассматривают математическое ожидание

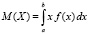(5.1)

и дисперсию

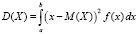. (5.2)

Интегралы (4.1) и (4.2) вводятся как естественные аналоги соответствующих числовых характеристик (2.2) и (2.3) дискретных случайных величин.

5.2. Из определения дисперсии (4.2) и свойства неотрицательности f(x) вытекает оценка 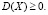Значит, может быть введено среднее квадратическое отклонение непрерывной случайной величины

.

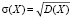Формула для вычисления дисперсии, аналогичная (2.3), имеет вид

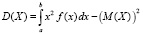. (5.3)

Доказательство (5.3), использующее свойства интегралов, может быть предложено учащимся в качестве теоретического упражнения.

5.3. К стандартным задачам на распределение НСВ относятся следующие:

1) по известной функции (плотности) распределения найти плотность (функцию) распределения;

2) найти значение параметра, присутствующего в аналитическом выражении, с помощью которого задается интегральная или дифференциальная функция;

3) найти вероятность принятия случайной величиною значений в заданном интервале;

4) найти числовые характеристики НСВ.

Рассмотрим пример комплексной задачи включающей все перечисленные позиции.

Пример. Плотность распределения задана в виде

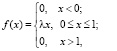
где λ – постоянная величина. Найти значение λ, функцию распределения F(x), вероятность того, что дважды в двух опытах данная случайная величина примет значение в интервале 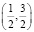, математическое ожидание и дисперсию.

Приведем возможную систему наводящих вопросов и заданий учителя при управлении решением этой задачи.

1) На каком отрезке распределена данная НСВ?

2) Каким свойством плотности распределения следует воспользоваться, чтобы найти неизвестный параметр?

3) Чем является функция распределения по отношению к плотности распределения? Каковы ее значения вне носителя распределения?

4) Как можно найти в совокупности первообразных (для f(x) на отрезке [0, 1]) постоянное слагаемое (постоянную интегрирования)?

5) По какой из двух возможных формул в данном задании будет проще найти вероятность принятия случайной величиной значения в интервале 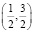? Как затем найти вероятность принятия таких значений дважды в двух опытах?

6) Записать формулы для вычисления математического ожидания, дисперсии. Произвести соответствующие вычисления.

6. Специальные распределения

Ввиду необходимости использования аппарата сходящихся рядов и несобственных интегралов возможности рассмотрения специальных распределений в школьном курсе (даже в классах с углубленным изучением математики) являются весьма ограниченными; альтернативные возможности представлены ниже.

6.1. Задача о специальных распределениях возникает как задача об «ассоциированной» случайной величине в знакомых учащемуся стандартных вероятностных схемах, что демонстрируется в следующей табл. 3 соответствия (комментарии представлены ниже).

6.2. Построение ряда распределения и функции распределения индикатора η = η(A) случайного события А с заданной вероятностью p(A) = p, а также нахождение числовых характеристик M(η) и D(η) могут быть предложены учащимся в качестве теоретического упражнения. Получаемые ряд и функция распределения будут иметь соответственно вид

(где q = 1 – p) и

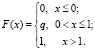
Далее,

,

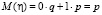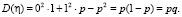
6.3. Равномерное распределение ДСВ изучено в п. 2.3, 2.5. Полезно предложить учащимся привести примеры равномерных распределений ДСВ и вычислить соответствующие числовые характеристики.

6.4. Вводя биномиальное распределение, т.е. распределение дискретной случайной величины Х, которая принимает значения, равные количеству появлений события А в п испытаниях, следует

а) повторить с учащимися характерные признаки схемы Бернулли и формулу Бернулли;

б) выделить параметры распределения: число опытов п, вероятность р наступления события в каждом опыте и его ненаступления q = 1 – p.

Поскольку 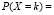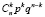, то соответствующий ряд распределения имеет вид

Построение биномиального ряда распределения сопровождается следующими вопросами.

1) Какие значения может принять биномиальная случайная величина при проведении п опытов?

2) Чему равна вероятность наступления события 0 раз (ни разу), ровно 1 раз, …, п раз?

3) Как проконтролировать, верно ли найдены вероятности во второй строке ряда распределения?

4) Привести примеры случайных величин, распределенных по биномиальному закону.

Далее, вводятся следующие правила: математическое ожидание биномиальной случайной величины Х равно произведению числа испытаний на вероятность появления события в одном испытании

,

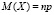а её дисперсия равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании

.

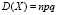Следует обратить внимание учащихся на возможность нахождения здесь математического ожидания и дисперсии без записи самого ряда распределения (т.е. без вычисления вероятностей Бернулли).

Не приводя строгого доказательства указанных формул, можно предложить одну из возможных его идей. Если через ηi обозначить индикатор появления события в i-м опыте, то наступление события ровно k раз означает, что k (из п) индикаторов примут значение, равное 1, тогда как остальные n – k примут значения, равные нулю. В итоге, число k наступлений события будет равно сумме п указанных слагаемых (единиц и нулей), а тогда, как оказывается, математическое ожидание M(X) складывается из всех п значений 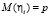, т.е. равно np.

Аналогичны рассуждения для обоснования формулы вычисления дисперсии D(X).

Пример. С какой вероятностью может появиться событие А в каждом опыте, если число появлений события распределено по биномиальному закону с математическим ожиданием, равным 20, и средним квадратическим отклонением, равным 4?

В процессе решения данные задачи могут быть записаны в виде системы уравнений

,

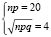откуда q = 0,8 и, следовательно, p = 1 – q = 0,2.

6.5. Если одинаковые опыты проводятся до первого наступления события А, имеющего в каждом опыте одну и ту же вероятность p = p(A), 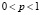и при этом q = 1 – p, то ассоциированной случайной величиной Х (геометрически распределенной ДСВ) является число опытов, проведенных до первого появления события А.

Построение ряда распределения сопровождается следующими вопросами.

1) Каковы возможные значения случайной величины Х ?

– Ответ: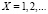

2) Чему равны вероятности ?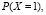

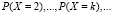– Ответ:

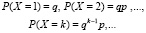
3) Охарактеризуйте последовательность вероятностей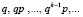

– Ответ: полученная последовательность – это бесконечно убывающая геометрическая прогрессия с первым членом, равным q, и знаменателем, равным p.

4) Привести примеры случайных величин, распределенных по геометрическому закону.

– Ответ: например, число вопросов, заданных экзаменатором студенту, до первого верного ответа, если правильный ответ на любой вопрос студент может дать с вероятностью p = 0,5.

Далее следует записать формулы для нахождения числовых характеристик геометрического распределения

,

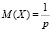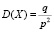
(доказательство не приводится, указывается лишь, что оно основано на суммировании членов бесконечно убывающей геометрической прогрессии) и найти эти характеристики в геометрических распределениях, которые приведены учащимися в качестве примеров.

6.6. Если равномерно распределенная ДСВ имеет одну и ту же (постоянную) вероятность каждого своего возможного значения, то ее «непрерывным» аналогом является НСВ, имеющая постоянную плотность на некотором отрезке [a, b]:

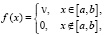
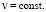
Значение постоянной ν определяем, используя свойство нормированности (теоретическое упражнение для учащихся); в результате получаем

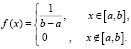
Функция распределения F(x) в случае 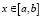определяется как одна из первообразных

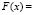
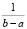х + С,

где значение постоянной С, в свою очередь, можно найти из условия F(a) = 0. Тогда

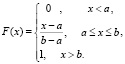
Далее может быть приведено следующее важное свойство НСВ, равномерно распределенной на отрезке [a, b]: для любых двух точек 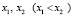отрезка [a, b] имеет место соотношение

.

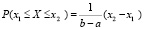Действительно,

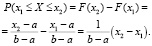
Следует прояснить смысл полученного результата: вероятность попадания значения равномерно распределенной НСВ в некоторый интервал носителя, пропорциональна длине этого интервала и не зависит от его расположения на носителе.

Формулы для вычисления математического ожидания и дисперсии случайной величины Х,

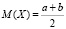и ,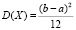

равномерно распределенной на отрезке [a, b], могут быть самостоятельно выведены учащимися.

Следует сообщить учащимся, что равномерные распределения довольно часто встречаются на практике. Например, равномерно распределение на отрезке [0; t0] время ожидания транспорта, если предположить, что пассажир приходит на остановку в случайный момент времени, а транспорт ходит регулярно с интервалом t0 мин. При компьютерном моделировании случайных явлений используется так называемый «генератор случайных чисел», который генерирует значения случайной величины, распределенной равномерно на отрезке [0; 1].

Пример. На каком интервале распределена случайная величина Х, если известно, что на этом промежутке ее плотность распределения равна 2, а среднее значение равно ?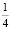

Решение основано на связи значений a и b (концы интервала) с плотностью распределения и математическим ожиданием. Если записать соответствующие формулы, то приходим к системе уравнений

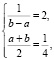
решив которую получаем a = 0 и 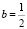. Итак, носителем распределения является интервал .

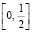6.7. Непрерывная величина Х, распределенная по показательному закону (с параметром λ > 0) с плотностью

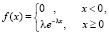
может служить примером распределения на бесконечном промежутке.

Нахождение интегральной функции F(x) учащиеся могут произвести самостоятельно уже известным им методом: при x ≤ 0 имеем F(x) = 0, а при x > 0 получим совокупность первообразных 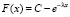. Из условия F(x) = 0 определяется значение C = 1, так что

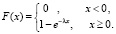(6.1)

Привычное свойство равенства единице значения F(x) на правом конце носителя Х (который здесь «отнесен в бесконечность») в случае (6.1) заменяется следующим предельным соотношением

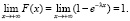
Вычисление математического ожидания (среднего значения) и дисперсии случайной величины, распределенной по показательному закону, связано с интегрированием по бесконечному промежутку, поэтому соответствующие формулы

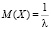и .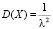

приводятся без доказательства. Стоит обратить внимание учащихся на следующее важное свойство: математическое ожидание здесь совпадает со значением среднего квадратического отклонения и равно величине, обратной параметру λ.

Показательный закон распределения широко применяется в теории массового обслуживания и в теории надежности.

Пример. Дисперсия показательного распределения величины Х равна 0,64. Какова вероятность, что значение Х отклонится от своего среднего значения не более, чем на 0,2?

В процессе решения учащимся предстоит ответить на следующие вопросы:

1) В каком интервале НСВ должна принять свое значение?

2) Как найти концы интервала, если известно значение D(X)?

3) Как найти соответствующую вероятность?

Рассуждения могут быть следующими. Среднее значение, или математическое ожидание, здесь равно 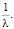Отклонения значений («влево» или «вправо») не более, чем на 0,2, означает принятие величиною Х значений в интервале 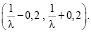При этом 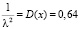, откуда 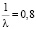и 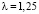. Значит, следует найти вероятность 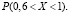Если учесть, что при 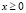функция распределения здесь будет иметь вид 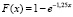, то

=

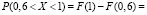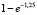
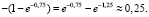
7. Нормальное распределение

Нормальный закон распределения наиболее распространен на практике, являясь предельным законом, к которому приближаются другие распределения при весьма часто встречающихся типичных условиях. По нормальному закону обычно распределена случайная величина, значения которой складываются из значений большого количества значений других случайных величин, и при этом ни одна из величин-слагаемых не должна доминировать (каждая из них играет в сумме примерно одинаковую роль). Так, например, отклонения Х контролируемого размера деталей от стандарта (при изготовлении их на станке-автомате) подчинены нормальному закону. Объясняется это тем, что на эти отклонения влияют многие причины, которые более или менее независимы друг от друга: неравномерный режим обработки детали, неоднородность обрабатываемого материала, неточность установки заготовки в станке, износ режущего инструмента и деталей станков, упругие деформации узлов станка, состояние микроклимата в цехе, колебание напряжения в электросети и т.д.

Указанное обстоятельство делает целесообразным ознакомление с нормальным распределением уже в школьном курсе на доступном учащимся уровне.

7.1. Рассмотрение можно начать с так называемого стандартного нормального распределения, т.е. распределения непрерывной случайной величины Х на всей числовой оси с плотностью (называемой также функцией Лапласа)

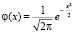. (7.1)

Затем на координатной плоскости изображают так называемую нормальную (гауссову) кривую, т.е. график функции y = φ(x), сопровождая построение следующими элементами исследования:

1) φ(x) > 0 для всех x;

2) функция y = φ(x) является четной, так что ее график симметричен относительно оси ординат;

3) при 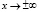значения φ(x) стремятся к нулю, т.е. ось абсцисс является горизонтальной асимптотой нормальной кривой;

4) функция y = φ(x) имеет максимум в точке x = 0, и при этом ее максимальное значение равно .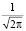

Первообразные для (7.1) не выражаются через элементарные функции. В качестве одной из первообразных для (6.1) рассматривается интегральная функция Лапласа – стандартный интеграл (с переменным верхним пределом)

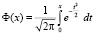. (7.2)

Следует ознакомить учащихся с таблицами значений функций (7.1) и (7.2) и подчеркнуть возможности их широкого использования (например, для приближенного вычисления вероятности Бернулли), а также обратить внимание на свойство нечетности функции (7.2).

7.2. В общем случае плотность нормального распределения определяется двумя параметрами a и σ > 0 и имеет вид

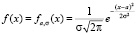, (7.3)

а функция распределения F(x) выражается через интегральную функцию Лапласа в виде

.

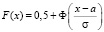По отношению к стандартной нормальной кривой график 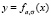получается ее преобразованием в 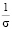раз вдоль оси абсцисс (преобразование растяжения или сжатия) и параллельным переносом вдоль этой оси на а единиц. Учащиеся могут сделать следующие выводы: в общем случае нормальная кривая симметрична относительно прямой x = a и имеет максимум в точке x = a, равный .

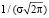Далее следует отметить, что вычисление математического ожидания и дисперсии нормального распределения связано с вычислением интегралов по всей числовой оси (термин «несобственный интеграл» вводить представляется нецелесообразным); при этом выясняется вероятностный смысл параметров а и σ: нормально распределенная случайная величина имеет математическое ожидание (среднее значение) M(X) = a и дисперсию D(X) = σ2.

7.3. Задача о вероятности попадания значений случайной величины Х, распределенной по нормальному закону, в промежуток 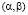относится к стандартным и может быть решена с помощью формулы

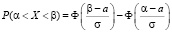. (7.4)

Действительно, если воспользоваться видом функции распределения (7.3), то получим

,

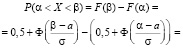
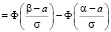что и утверждалось.

Целесообразно предложить учащимся несколько задач на нахождение таких вероятностей, что способствует приобретению навыка работы с таблицами значений функций Лапласа.

7.4. Вывод формулы

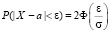, (где ε > 0) (7.5)

для нахождения вероятности заданно малого отклонения значений нормальной величины от среднего значения может быть предложен учащимся в качестве теоретического упражнения. Ключевыми моментами здесь являются запись неравенства 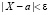в равносильном виде 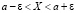, использование формулы (7.4) и свойства нечетности интегральной функции Лапласа.

В частности при ε = 3σ получаем так называемое правило «трех сигм»

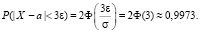
Смысл его состоит в следующем: практически достоверно, что абсолютная величина отклонения значений нормально распределенной Х от параметра а меньше утроенного значения σ.

8. Эмпирическое распределение. Связь с теоретическим распределением

8.1. В школьном курсе значительное внимание уделяется анализу распределения случайной величины, представленного выборочной совокупностью, а именно, построению по выборочным данным вариационных рядов, полигонов и гистограмм распределения, нахождению моды и медианы и других числовых характеристик. Однако, как указано выше, каждое такое распределение представляет собою некий «срез» распределения количественного признака всей генеральной совокупности (так называемого теоретического распределения). Целью изучения выборок как раз и является получение информации о теоретическом распределении. Здесь основанием для каких-либо выводов является так называемый закон больших чисел. Суть закона состоит в том, что при некоторых условиях суммарное поведение достаточно большого числа случайных величин (здесь это будет набор случайных величин 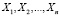, в каждом случае выборки представленным наблюдаемыми значениями 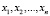) утрачивает случайный характер и становится в некотором смысле предсказуемым.

Одним из важнейших средств, устанавливающих связи между теоретическим и эмпирическим распределениями является в первую очередь теорема (закон) Бернулли, которая утверждает следующее. Последовательность относительных частот наступления случайного события А

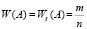
(n – число проведенных опытов, 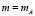– число наступлений события А в этих опытах) «сходится по вероятности» к вероятности р = р(А) данного события. А именно, с уверенностью, сколько угодно близкой к 100 %, можно утверждать, что относительная частота появления события А заданно мало отклонится от его вероятности, если число проведенных опытов достаточно велико. Заметим, что при этом число опытов п определяется как заданной близостью уверенности к 100 % (близостью вероятности к единице), так и заданно малым отклонением ε.

8.2. Практическое использование закона Бернулли состоит в установлении связи эмпирических и теоретических распределений случайных величин, о которой пойдет речь в данном параграфе (см. табл. 4).

Ключевыми здесь являются следующие понятия: генеральная совокупность (возможно, и бесконечная), количественный признак X генеральной совокупности (масса объектов, размер изделий, возраст пациентов и т.д.) – случайная величина с неизвестной нам функцией распределения вероятностей F(x), выборочная совокупность (выборка), объем выборки.

Алгоритм анализа эмпирического распределения выборки предлагается в действующих учебниках и задачниках (см., напр., [5, 6]), в силу чего останавливаться на этом алгоритме здесь не будем.

Как указано в табл. 4, вариационный ряд (в терминах относительных частот) служит эмпирическим (статистическим) аналогом ряда распределения ДСВ, а относительные частоты wi значений xi дают первичное представление о вероятностях 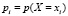случайных событий X = xi. Точнее, в силу закона Бернулли, с ростом объема выборки п относительные частоты сходятся по вероятности к вероятностям соответствующих событий.

8.3. Понятие эмпирической функции распределения 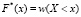предлагается учащимся в качестве статистического аналога функции распределения ДСВ. Ее построение учащиеся могут осуществлять на основе принципа накопления относительных частот, аналогичного принципу накопления вероятностей.

Из закона больших чисел Бернулли вытекает сходимость (при 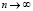) «по вероятности» последовательности эмпирических функций 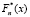к функции теоретического распределения F(x). Следовательно, при больших n эмпирическая функция распределения может быть использована для приближенного представления интегральной функции теоретического распределения.

8.4. Среднее арифметическое наблюдаемых в выборке значений и степень рассеяния значений относительно их среднего (выборочная средняя 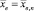и выборочная дисперсия Dв = Dв,п соответственно) вводятся как статистические аналоги математического ожидания и дисперсии ДСВ. Нахождение соответствующих характеристик вариационного ряда обычно не представляет затруднений для учащихся.

На основании сходимости (по вероятности) относительных частот событий X = xi к вероятностям соответствующих событий можно утверждать, что 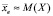. В более точной формулировке, последовательность значений выборочных средних 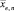сходится по вероятности к значению математического ожидания M(X), а именно с уверенностью, сколько угодно близкой к 100 %, можно утверждать, что выборочная средняя заданно мало отклонится от математического ожидания количественного признака Х, если объем выборки будет достаточно велик.

Аналогичным образом последовательность значений выборочных дисперсий Dв,п сходится по вероятности к значению дисперсии теоретического распределения D(X).

8.5. Теоретическое распределение количественного признака Х генеральной совокупности характеризуется некоторыми параметрами; так, биномиальное распределение характеризуется параметрами р и п, нормальное распределение – параметрами а и σ и т.д. Одна из задач статистики – получить информацию о значениях параметров распределения на основе анализа выборки.

В школьном курсе понятие точечной оценки параметра q теоретического распределения следует рассматривать в упрощенном виде: оценка есть найденное на основе анализа выборки приближенное значение q. В основе получения точечных оценок лежит закон больших чисел (и, в частности, закон Бернулли). Так, например, в качестве точечной оценки математического ожидания 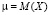количественного признака Х генеральной совокупности предлагается значение выборочной средней. Точечной оценкой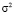 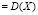является выборочная дисперсия; соответственно, точечной оценкой параметра σ является выборочное среднее квадратическое отклонение.

Школьникам также доступна идея нахождения точечных оценок неизвестных параметров на основе метода моментов: решение уравнения 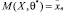относительно неизвестной 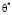или системы уравнений

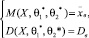
относительно .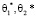

Заключение

Основные результаты настоящей работы состоят в следующем.

1. В качестве возможного элемента обновления содержания математического образования в старшей школе (профильный уровень) может быть предложен модуль «Случайные величины».

2. Выстроен пошаговый алгоритм анализа распределений дискретных случайных величин.

3. Алгоритм исследования распределений непрерывных случайных величин адаптирован к школьному курсу, что позволило избежать использования инструментария несобственных интегралов.

4. Введены распределения специальных величин как «ассоциированных» случайных величин в знакомых учащемуся стандартных вероятностных схемах.

5. Предложен подход к изучению выборок как к средству извлечения информации о соответствующем теоретическом распределении.

Библиографическая ссылка