Современное состояние проблемы
Становление современной образовательной парадигмы связано с изменением знание-ориентированного подхода в преподавании учебных дисциплин на компетентностный, с формированием у обучающихся современной функциональной грамотности, развитием умений к поиску новых знаний, их критическому анализу и интеграции, способностей к жизни и деятельности в условиях неопределённости.
Идея наполнения школьного курса задачами «реальной математики» не является новой, однако проблема выстраивания «сквозной» линии математических моделей, формирования соответствующего содержания и технологий нуждается в дальнейшей разработке. Среди формируемых компетенций важное место занимает компетенция математического моделирования. Формирование данной компетенции у обучающихся неразрывно связано с ее развитием у учителя математики. В последнем случае правильнее говорить о компетентности в области математического моделирования. Одной из задач настоящей работы является выявление сравнительных характеристик компонент данной компетенции/компетентности у обучающегося и педагога.
Понятие компетенции математического моделирования введено в педагогическую теорию сравнительно недавно [14]. В компетентностном «портрете» выпускника вуза данная компетенция играет значительную роль, поскольку математическое моделирование становится рабочим инструментом не только в цикле естественно-научных дисциплин, но и в дисциплинах, традиционно считающихся гуманитарными (лингвистика, юриспруденция и др.). Так, в работе [14] (посвященной вопросам обучения студентов-менеджеров), отмечается, что математическое моделирование «…является инструментом прогнозирования, оптимизации, количественного и качественного анализа, сбора и обработки профессионально-значимой информации, то есть средством управления экономическими процессами». Компетенция математического моделирования вводится автором как «способность и готовность применять математические знания и методы при построении математических моделей для повышения эффективности принимаемых управленческих решений». Структурными компонентами данной компетенции, по мнению автора, являются:
– математические знания;
– умения строить математические модели;
– интеллектуальные способности и профессионально значимые качества, необходимые для успешной деятельности специалиста;
– мотивационно-ценностное отношение к знаниям, умениям и навыкам в области построения математических моделей в профессиональной деятельности.
Вопросы формирование компетенции математического моделирования у студентов инженерных направлений подготовки рассмотрены в статье [11].
Работа [2] посвящена роли математических моделей в подготовке будущих учителей математики к исследовательской деятельности, овладении ими методологией научного исследования.
В монографии [5], статье [11] и обзоре [6] понятие компетенции математического моделирования адаптировано к системе «школа-вуз»; данная компетенция определяется как способность актуализировать и применять математические знания и умения при построении, анализе и интерпретации математических моделей в процессе решения учебных и практических задач. Развивая идеи [6] и [9], в настоящей работе мы вводим понятие компетентности педагога-математика в области математического моделирования.
Выделение линии моделей в отдельную содержательно-методическую линию школьного курса математики нераздельно связано с новым взглядом на традиционные модули. Речь идет о том, что многие базовые понятия и факты (например, понятия и факты математического анализа, см. [5], [10]) могут рассматриваться как средства моделирования.
В настоящем обзоре анализируется содержательное наполнение линии математических моделей и соответствующие компоненты содержания «увязываются» с системой знаний и умений педагога-математика. Поскольку поддержание квалификационного уровня компетентного специалиста предполагает постоянное обновление знаний и oвладение новой информацией, а также мотивацию к такому обновлению, предлагаются вопросы содержания программы повышения квалификации учителей математики по направлению «Линия математических моделей».
Современная образовательная парадигма и компетентностный подход
Парадигма образования традиционно понимается как совокупность ключевых понятий, положений и идей, которые признаны педагогической общественностью в конкретный период и лежат в основе научных исследований. Парадигмы на самом общем уровне можно разделить на устремленные в будущее («прогрессивные») и «классические». «Классической» обозначается устоявшаяся, традиционная, достаточно долго доминирующая в сфере образования парадигма. Современная (неклассическая) образовательная парадигма предполагает активную, творческую деятельность обучающихся (в отличие от традиционной передачи обучаемому известных образцов знаний, умений и навыков и взамен его «ответной», репродуктивной деятельности).
Коротко говоря, переход к современной образовательной парадигме есть переход от «школы памяти» к «школе мышления и действия». Это предполагает включение в содержание образования способов анализа ситуаций и разрешения проблем в новых условиях. Компетентностный подход в общем и профессиональном образовании – одна из существенных характеристик современной образовательной парадигмы. Суть его в том, что знания и умения должны быть мобильными, должны работать, носить прикладной и практико-ориентированный характер. Мобильность состоит в способности индивида применять багаж знаний и умений в новой ситуации, в новых условиях, при решении незнакомых задач, выходящих за рамки соответствующей предметной области. Переход к новой парадигме сопряжен с формированием и развитием новых компетенций как обучающегося, так и учителя. В частности, современная концепция предметной области «Математика» предполагает способность обучающегося установить связь между практической или прикладной задачей и математическим аппаратом (понятиями, утверждениями, фактами, алгоритмами), который может быть применен для решения данной задачи. Способность устанавливать такие связи мы и принимаем за рабочее определение компетенции математического моделирования.
В случае педагога-математика корректнее будет говорить о компетентности в области математического моделирования.
Понятия компетенции и компетентности по мнению одних авторов – неразличимы, по мнению других (напр., [16], [5] и др.) имеют существенные различия. Эти различия состоят в следующем.
1. В основе компетентности положена интегрированная модель, которая включает четыре уровня развития: знания (и их организация); умения (и их использование); интеллектуально-творческий потенциал человека; эмоционально-нравственные отношения с миром, включающие в себя психологическую готовность сотрудничать и взаимодействовать для решения различного спектра проблем.
2. Компетентность, предполагает готовность к определенному виду деятельности в отличие от компетенции, которая есть некий потенциал, способность к этому виду деятельности. Коротко говоря, компетентность есть «компетенция в действии», реализация потенциала. При этом человек, обладающий компетентностью, имеет достаточную квалификацию для превращения « ресурса в продукт».
3. Поддержание квалификационного уровня компетентного специалиста предполагает постоянное обновление знаний и овладение новой информацией, чтобы применять их во всех возможных условиях, а также мотивацию к такому обновлению.
Будем говорить теперь, что педагог-математик обладает компетентностью в области математического моделирования, если его квалификация позволяет говорить о высоком уровне развитии знаниевой и операционно-технологической составляющей деятельности по преподаванию линии математических моделей. Речь идет о готовности решать практические и прикладные задачи средствами математики и достаточной методической готовности включить обучающихся в этот вид математической деятельности. Данная готовность сопровождается высокой мотивацией к обновлению соответствующих знаний и умений (как в содержании предметной области, так и в методике преподавания), потребность в развитии интеллектуально-творческого потенциала, психологическую установку на плодотворное сотрудничество (с обучающимися и коллегами) в сфере построения, анализа и интерпретации математических моделей различных процессов и явлений.
Компоненты компетенции математического моделирования
Сравнительную характеристику компонент компетенции обучающихся и педагогов мы приведем, исходя из требований действующей нормативной базы, регламентирующей образовательный процесс:
– Концепции развития российского математического образования (далее – Концепция, [1]);
– Профессионального стандарта педагога (Вводится с 2017 г. Утвержден приказом Министерства труда и социальной защиты Российской Федерации от 18 октября 2013 г. № 544н; см. [13])
– ФГОС общего среднего и высшего профессионального образования; см. [15].
Выделим здесь те положения, которые согласованы (или напрямую заимствованы) с перечисленными документами (из перечисленных документов), относящиеся непосредственно к компетенции математического моделирования.
Согласно Концепции, «изучение и преподавание математики, с одной стороны, обеспечивают готовность учащихся к применению математики в других областях, с другой стороны, имеют системообразующую функцию, существенно влияют на интеллектуальную готовность школьников и студентов к обучению, а также на содержание и преподавание других предметов». Среди основных задач развития математического образования в Российской Федерации отмечается необходимость формирования у учащихся прикладных умений, в том числе – использовать математический подход в рассуждении, обосновании, аргументации, планировании, в пространственных построениях, численных оценках.
При этом основная задача педагогаматематика состоит в формировании у обучающихся модели соответствующей деятельности, в частности – умения и готовности решать средствами математики практические и прикладные задачи.
Среди трудовых действий, предписанных вновь вводимым профессиональным стандартом указываются:
– «формирование способности к постижению основ математических моделей реального объекта или процесса, готовности к применению моделирования для построения объектов и процессов, определения или предсказания их свойств»;
– «формирование у обучающихся умения пользоваться заданной математической моделью, в частности, формулой, геометрической конфигурацией, алгоритмом, оценивать возможный результат моделирования (например – вычисления)».
При этом педагогу-математику необходимо обладание
– знаниями основ математической теории и перспективных направлений развития современной математики, а также теории и методики преподавания математики;
– представлениями о широком спектре приложений математики и знанием доступных обучающимся математических элементов этих приложений;
В числе необходимых должны наличествовать умения:
– направлять действия обучающихся на построение цепочки логических рассуждений (например, при решении задачи) в математических и иных контекстах;
– направлять действия обучающихся при анализе учебных и реальных задач, в которых используются математические инструменты, в том числе при анализе таблиц, графиков, диаграмм, а также идеализированных (задачных) ситуаций, описанных текстом.
Таблица 1
Структурные компоненты компетенции/компетентности
|
Компоненты компетенции/компетентности математического моделирования |
Обучающийся: содержание компонента компетенции |
Учитель математики: содержание компонента компетентности |
|
1 |
2 |
3 |
|
Мотивационно-ценностное отношение к математическим знаниям и умению строить математические модели в процессе учебной и практической деятельности |
Понимание универсальности математического языка, знакомство со свойством универсальности ряда математических моделей, что способствуют росту мотивации математической деятельности. |
Осознание важности осваиваемых областей профессиональной деятельности: – исследовательской деятельности (в областях, использующих математические методы и компьютерные технологии); – педагогической (разработка методики решения средствами математики задач естествознания, экономики и др.). |
|
Кругозор |
Интерес ко всему происходящему в мире в настоящее время, к истории, к отечественной и зарубежной культуре, литературе, искусству, что неизбежно сопровождается анализом явлений и процессов, сравнительными характеристиками, логическими умозаключениями и т.п. В свою очередь, указанные формы мыслительной деятельности способствуют развитию умений выделять главное и отбрасывать второстепенное, кратко и ясно выражать свои мысли, ставить задачи, получать и четко формулировать выводы, а эти умения успешно «встраиваются» в процессы математического моделирования. |
Проявляется в способности использовать основы экономических, правовых, философских и др. знаний в различных сферах жизнедеятельности, а также в деятельности по воспитанию и обучению в интересах каждого обучающегося, общества, государства. |
|
Знания и умения |
Знание основ элементарной алгебры, геометрии, математической логики, математического анализа, стохастики. Умения: – актуализировать математические знания применительно к выстраиваемой модели в условиях конкретной ситуации; – умение выстраивать процесс решения задачи (постановка вопроса, нахождение нужной информации для решения задачи, анализ проблемной ситуации, выдвижение гипотезы, выбор алгоритма решения, пошаговое выполнение алгоритма, формулировка выводов); – способность к математизации объектов и процессов (определение данных, условий и границ поиска решений, перевод проблемы на язык математики, применение адекватного математического аппарата); – умение логически мыслить (дедуктивные и индуктивные умозаключения, комбинация логики и интуиции, аргументация выводов и заключений); – коммуникативные умения (чтение, письмо, речь на языке математики, использование математических символов и формул, построение графиков, схем, диаграмм); – умение применять современные информационные технологии. |
Знание основ фукционального анализа, алгебры, аналитической геометрии, дифференциальной геометрии и топологии, дифференциальных уравнений, дискретной математики и математической логики, теории вероятностей, математической статистики и теории случайных процессов, численных методов. Умение применять в теоретических и практических исследованиях понятия, гипотезы, теоремы, методы и математические модели, составляющие содержание фундаментальной и прикладной математики, механики и других естественных наук. |
|
Окончание табл. 1 |
||
|
1 |
2 |
3 |
|
Опыт математической деятельности |
Данный опыт способствует закреплению умений в форме навыков. На основе опыта, приобретенного в процессе решения учебных задач, возникает и развивается способность к переносу математических знаний и умений на незнакомые ситуации, в том числе, возникающие в практической деятельности. |
Данный опыт (в том числе знание постановок классических задач математики) способствует развитию умений корректно ставить естественнонаучные задачи, использовать методы математического и алгоритмического моделирования при решении теоретических и прикладных задач. |
|
Рефлексия |
Самооценка деятельности в области математического моделирования, что способствует развитию таких качеств учащегося, как самоконтроль, ответственность, рациональность, самостоятельность. |
Самооценка умения выстраивать пошагово процесс моделирования; фиксация успехов и недостатков в работе с обучающимися по решению задач математического моделирования, усиление стимулов к творческому поиску, воссоздание и анализ схем и средств прошлой деятельности (ретроспектива), выявление и корректировка схем и средств будущей деятельности (перспектива) |
Таблица 2
Нахождение нормального вектора плоскости
|
Вид плоскости |
Уравнение плоскости |
Нормальный вектор |
|
1. Плоскость, параллельная координатной плоскости (или совпадающая с ней) |
Плоскость, параллельная ХОУ (либо совпадающая с ней): z = a (z = 0) |
|
|
Плоскость, параллельная ХОZ (либо совпадающая с ней): y = a (y = 0) |
|
|
|
Плоскость, параллельная УОZ (либо совпадающая с ней): x = a (x = 0) |
|
|
|
2. Плоскость, проходящая через начало координат (отличная от координатных плоскостей) |
Ax + By + Cz = 0 (коэффициенты A, B, C определяются по трём различным точкам плоскости, отличным от начала координат) |
|
|
3. Плоскость, не проходящая через начало координат |
Ax + By + Cz = 1 (коэффициенты A, B, C определяются по трём различным точкам плоскости) |
|
|
В частности, плоскость
|
|
В следующей таблице представлены выделяемые нами структурные компоненты компетенции/компетентности в области математического моделирования и содержание компонент, обусловленное требованиями ФГОС общего образования (основное общее и среднее общее образование) к предметной подготовке обучающихся, а также требованиями ФГОС высшего профессионального образования по направлению подготовки 010100 математика (квалификация (степень) «бакалавр»).
Содержательная линия математических моделей в школьном курсе математики
Обладание новыми компетенциями предполагает освоение новых содержательных линий. В частности, компетенция математического моделирования предполагает освоение обучающимся содержательной линии математических моделей. Данная линия пронизывает весь школьный курс математики. Её особенность состоит в том, что она не предполагает изучение каких либо специальных модулей. Данная линия интегрирована с традиционными содержательными линиями: числа и вычисления, алгебра, функциональная линия, геометрия, начала анализа, элементы стохастики. В рамках каждой содержательной линии на этапе постановки проблемы может быть предложена какая-либо практическая задача, либо задача из смежной предметной области (например, физики).
Отработка навыков решения типовых задач (например, уравнений и неравенств и их систем) может происходить в рамках решений опять-таки прикладных и практических задач. Широкие возможности для такой деятельности предоставляет, например, открытый сегмент банка контрольно-измерительных материалов ГИА (ОГЭ и ЕГЭ).
Содержательная линия математических моделей в школьном курсе математики может быть представлена следующими её компонентами:
– арифметико-алгебраический компонент;
– логико-алгоритмический компонент;
– геометрический компонент;
– аналитический (теоретико-функциональный) компонент;
– стохастический компонент.
Арифметико-алгебраический компонент реализуется, например, в виде традиционных текстовых задач, решаемых «арифметическим способом» (т.е. непосредственным вычислением искомого значения посредством выполнения арифметических действий без записи уравнений) или алгебраическим путём: составление уравнений либо их систем, и их решение с использованием алгебраических преобразований. Важным и актуальным видом таких задач являются задачи финансовой математики. Заметим, что при решении этих же задач реализуется и логико-алгоритмический компонент, а именно, конструируется цепочка логических умозаключений, приводящих к выстраиванию плана решения.
Геометрический компонент реализуется посредством решения задач «прикладной геометрии», представленных, например, в открытом сегменте контрольно-измерительных материалов ОГЭ [12]. Здесь формализация задачи происходит посредством описания геометрического объекта и выявления соответствующих геометрических свойств и следующих из них фактов. Далее следует «внутримодельное» решение и простейшая интерпретация результатов.
Аналитический (теоретико-функциональный) компонент широко представлен задачами на чтение графиков, построение графиков и выявления свойств изучаемых зависимостей, заданиями на нахождение наибольших и наименьших значений величин, задачами оптимизации.
Наконец, стохастический компонент представлен простейшими заданиями на анализ экспериментальных данных (анализ эмпирических распределений) и вычисления вероятностей случайных событий на основе подходящей модели вероятности (классической, статистической, геометрической).
Изучение «реальной математики», по нашему мнению, не усугубит проблему дефицита учебного времени, если традиционные, «формально-математические» (и, порою, однотипные) задачи в значительной степени заменить прикладными или практико-ориентированными задачами на ту же (изучаемую в данный момент) тему, причём на всех этапах ее освоения: при постановке проблемы, приводящей к тем или иным понятиям и фактам, затем – на этапе отработки умений и закреплении навыков, и, наконец, на этапе контроля. Так, например, при изучении кусочно-линейных функций (а, вместе с этим, и при формировании первичных представлений о непрерывности и точках разрыва) может быть предложена следующая задача.
В стране N установлена следующая система налогообложения: годовая прибыль в размере до 1000 у.е. налогом не облагается; первые 1000-5000 у.е. чистой прибыли облагаются фиксированным налогом в 100 у.е., а суммы, полученные сверх 5000 у.е., облагаются по ставке 15 %.
1. Какую сумму налога должен уплатить предприниматель, получивший 5000 у.е.; 50000 у.е.
2. Получите аналитическое выражение функции y = f(x), где х – размер чистой прибыли.
3. Постройте график функции y = f(x). Каковы ее область определения и множество значений Является ли функция непрерывной
К проблеме развития компетентности педагогов-математиков в области математического моделирования
При рассмотрении проблемы развития компетентности педагогов в области математического моделирования следует отметить, что объём соответствующих знаний и умений должен быть существенно расширен в сравнении с теми, что приобретает обучающийся при освоении линии моделей.
Так, владение арифметико-алгебраическим компонентом означает, что учитель обладает знанием оснований арифметики, алгебраических структур, теории многочленов и др., а также имеет представление об областях их применения в современной науке и практике.
Владение логико-алгоритмических компонентом предполагает знание алгебры и исчисления высказываний, логики предикатов, основ теории алгоритмов, а также представление о нечеткой логике и областях её применения. Помимо знаний и необходимых умений в области решения типовых задач, учитель должен владеть средствами применения этих знаний и умений в логико-математической практике, а именно, владеть:
– навыками формулирования необходимых и достаточных условий, навыками формулирования обратных и противоположных утверждений к известным теоремам (речь идет о следовании предикатов, операциях отрицания предикатов);
– логическими операциями над предикатами;
– понятиями следования и равносильности предикатов, и, в частности, навыками равносильных переходов в уравнениях и неравенствах.
Чрезвычайно важен здесь и методический аспект: убедительное объяснение учащимся отличий уравнения-следствия от равносильного уравнения, системы неравенств от их совокупности и др.
Владение геометрическим компонентом предполагает наличие знаний и умений в области аналитической геометрии, что важно в процессах «внутрипредметного» моделирования. В частности, речь идет о решении задач стереометрии повышенной сложности векторно-координатным способом. Так, например, векторно-координатный метод может быть применен к следующей задаче.
В кубе ABCDA1B1C1D1 точки E и F – середины ребер, соответственно, A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
В вопросах объема изучаемого со школьниками соответствующего материала необходимо соблюдать «разумную меру», чтобы не дублировать вузовский курс аналитической геометрии (такое дублирование приводит к неоправданным затратам времени и усилий обучающихся).
Остановимся на методическом аспекте. В вышеприведённом задании, как и в ряде других, основную трудность представляет нахождение нормального вектора плоскости. Поскольку в школьном курсе не изучаются векторное и смешанное произведения векторов, требуется элементарный путь нахождения такого вектора. Метод, предлагаемый в традиционных школьных учебниках, нам представляется «непрозрачным» и, обычно, вызывает затруднения обучающихся ввиду использования в уравнениях «свободной» переменной. Альтернативным может служить предлагаемый нами метод, основанный на «селекции» видов плоскостей.
В системе знаний и умений педагога-математика овладение аналитическим (теоретико-функциональным) компонентом компетентности в области математического моделирования, предполагает, что наряду с дифференциальным и интегральным исчислением функций одной переменной учитель владеет знаниями и умениями в области:
– дифференциального исчисления функций нескольких переменных и его применения в векторном анализе;
– интегрального исчисления функций нескольких переменных (кратные интегралы и их применение в геометрии и механике);
– криволинейных интегралов по длине дуги и координатам и их применения, соответственно, при вычислении масс линий и работы заданной силы;
– дифференциальных уравнений и их применения в задачах физики, экономики и др.;
– гармонического анализа, и, в частности, применения рядов Фурье в моделировании процессов колебаний, теплопроводности, диффузии.
Наиболее приближен к практике стохастический компонент компетентности в области математического моделирования. Запас знаний и умений педагога-математика не должен исчерпываться простейшими теоремами о вероятностях случайных событий и умениями вычислять такие вероятности, а также решать простейшие задачи на анализ статистических данных. Необходимо понимание того факта, что действия над событиями служат одной из возможных интерпретаций операций над элементами булевых алгебр ([3]), что, в свою очередь, позволяет правильно выстроить формулу для подсчета искомой вероятности ([4],[8]). Важно также владение теорией случайных величин и осознание глубокой связи случайных событий со случайными величинами. В частности, необходимо уметь моделировать данное распределение случайной величины в виде ряда или функции (плотности) распределения, визуализировать распределение (строить многоугольники распределения, кривые распределения), находить числовые характеристики (среднее значение, дисперсию) и др. ([7]). Владение стандартными распределениями (равномерное, биномиальное, пуассоновское, показательное, нормальное), наиболее часто встречающимися на практике, позволит педагогу осознать (и поделиться соответствующей информацией с обучающимися) возможности практического использования фундаментальных законов стохастики: закона больших чисел и центральной предельной теоремы. В свою очередь, такое осознание способствует пониманию вероятностного смысла числовых характеристик эмпирических распределений и их графических интерпретаций (полигон, гистограмма).
Наконец, учителю математики необходимо владеть хотя бы в общих чертах, основами корреляционного и регрессионного анализа. В целом, знание всех перечисленных аспектов вероятностно-статистической теории позволяют учителю (а вместе с ним и обучающимся) получить представление о математических методах прогнозирования поведения недетерминированных моделей и принятия оптимальных управленческих решений в ситуациях неопределенности.
Вопросы содержания программы повышения квалификации по направлению «Линия математических моделей»
1. Научно-практические подходы к реализации Концепции развития математического образования.
Цели математического образования. Возможные меры по стимулированию социального заказа «снизу» на математическое образование, усилению мотивации к математической деятельности. Сочетание лучших традиций отечественного математического образования и современных образовательных инноваций как концептуальная основа совершенствования математического образования. Уровневая модель системы мероприятий по реализации Концепции в регионе. Совершенствование кадрового потенциала. Роль системы повышения квалификации в реализации Концепции.
2. Формирование мотивации учения на основе построения математических моделей реальных событий.
Математические модели как средство мотивации математической деятельности. Понятие модели на интуитивном уровне. Математическое моделирование: концепция и этапы. Детерминированные и стохастические модели. Свойство универсальности математических моделей.
Мастер-класс. Участникам мастер-класса предлагается рассмотреть основные приемы по формированию мотивации учения на основе построения математических моделей реальных событий, выявить основные типы соответствующих задач школьного курса. Материал рассматривается на примере урочной и внеурочной деятельности.
3. Методика подготовки обучающихся к сдаче ГИА по математике (задачи реальной математики).
3.1. Текстовые задачи и систематизация методов их решения.
Мастер-класс. В ходе мастер-класса рассматриваются основные проблемы, возникающие у обучающихся в процессе решения текстовых задач. Выделяются этапы решения задач, рассматривается их типология и методы их решения. Слушателям предлагается пройти тестирование на определение типа задачи и решить задачи, которые наиболее часто вызывают затруднения у обучающихся.
3.2. Особенности решения задач оптимизации и «финансовой математики».
Мастер-класс. В ходе мастер-класса рассматриваются подходы к решению задач финансовой математики (от простейших задач до задач высокого уровня сложности) и методы «максимизации» и «минимизации».
3.3. Векторно-координатный метод при решении задач стереометрии.
Тренинг по решению задач. В ходе тренинга рассматривается следующая тематика:
– приёмы составления уравнений плоскости;
– задачи по теме «Угол между прямыми в пространстве»;
– задачи по теме «Угол между прямой и плоскостью;
– задачи по теме «Угол между плоскостями»;
– задачи по теме «Расстояние от точки до прямой»;
– задачи по теме «Расстояние от точки до плоскости».
4. Содержательные приоритеты и организационные формы различных направлений внеурочной деятельности по математике.
Цель и задачи внеурочной деятельности. Формы внеурочной работы по математике. Формы работы с высокомотивированными обучающимися. Создание системы элективных курсов в образовательной организации. Профессионально-личностная квалификация педагогов для работы с высокомотивированными обучающимися.
5. Сетевой круглый стол.
5.1. Обобщенный анализ успешности выполнения практических заданий, предлагавшихся слушателям в рамках курсов, с разбором типичных ошибок и рекомендациями по их предупреждению в образовательной деятельности.
5.2. Анализ результатов проектирования содержания линии математических моделей.
Выводы
1. Формирование компетенции математического моделирования компетенции у обучающихся неразрывно связано с развитием соответствующих предметных знаний и методических умений учителя математики.
2. В контексте современной образовательной парадигмы необходимо развитие компетентности педагога-математика в области математического моделирования; введено понятие такой компетентности.
3. На основе положений основных нормативных документов выявлена сравнительная характеристика компонент компетенции/компетентности математического моделирования у обучающихся и педагогов.
4. Представлено содержательное наполнение линии математических моделей, при изучении которой формируется компетенция математического моделирования у учащегося / реализуется соответствующая компетентность у педагога. Предложены некоторые практические рекомендации. Предложены также вопросы содержания программы повышения квалификации учителей математики по направлению «Линия математических моделей».
Библиографическая ссылка
Нахман А.Д. КОМПЕТЕНЦИЯ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ В КОНТЕКСТЕ СОВРЕМЕННОЙ ОБРАЗОВАТЕЛЬНОЙ ПАРАДИГМЫ // Научное обозрение. Педагогические науки. 2017. № 3. С. 71-79;URL: https://science-pedagogy.ru/ru/article/view?id=1625 (дата обращения: 17.02.2026).


 science-review.ru
science-review.ru
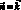 , т.е. n{0, 0, 1}
, т.е. n{0, 0, 1}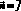 , т.е.
, т.е.  {0, 1, 0}
{0, 1, 0}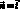 , т.е.
, т.е.  {1, 0, 0}
{1, 0, 0} {А, В, С}
{А, В, С} {А, В, С}
{А, В, С}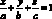 , отсекающая на каждой из трёх координатных осей невырожденные отрезки величины a, b, c.
, отсекающая на каждой из трёх координатных осей невырожденные отрезки величины a, b, c.