science-review.ru
Важнейшим компонентом в «компетентностном портрете» выпускника средней школы является сформированность навыков математического моделирования. Соответствующий социальный запрос нашел свое отражение в требованиях Федерального государственного образовательного стандарта (далее – ФГОС) к математической подготовке учащегося старшей школы [25, 26], согласно которым «изучение предметной области «Математика» должно «обеспечить осознание значения математики … в повседневной жизни человека…, математики – как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления».
Аналогичные ориентиры обозначены и в Концепции развития Российского математического образования [9]: «…изучение и преподавание математики, с одной стороны, обеспечивают готовность учащихся к применению математики в других областях, с другой стороны, имеют системообразующую функцию, существенно влияют на интеллектуальную готовность школьников и студентов к обучению, а также на содержание и преподавание других предметов».
Навыки математического моделирования занимают важное место среди общих результатов освоения учащимися основной образовательной программы (личностные характеристики, результаты метапредметного характера), и предметных результатов. Востребованность таких навыков обусловлена тем, что математическое моделирование, благодаря бурному развитию вычислительных методов, становится одним из основных методологических подходов к исследованию разнообразных реальных процессов, становясь все более универсальным. В этой связи усилилась необходимость модернизации математического образования [8], целью которого является уже не только приобретение учащимися некоторой суммы математических знаний, но, в первую очередь, развитие логического мышления, освоение математического аппарата, необходимого для решения прикладных и практических задач, выработка умений перевести задачу с практическим содержанием на математический язык. В решении таких задач заложен наибольший потенциал для роста мотивации учащихся к математической деятельности. Мотив рождается как следствие осознания учащимися возможностей математической науки в описании, исследовании, прогнозировании характера происходящих процессов и явлений. Эта мысль неоднократно высказывалась многими ведущими математиками (А.Н. Колмогоров, Б.В. Гнеденко и др.; см. статью [24] и библиографию в ней). Например, известный учёный и педагог Н.Я. Виленкин, говоря о проблемном методе обучения, рекомендовал постановку проблемы предварять какой-либо прикладной задачей. В этом случае у учащегося не возникнет представления об оторванности математики от практической деятельности человека.
Каждая практическая или прикладная задача, решаемая средствами математики, сопровождается переводом ее условия на математический язык и последующим использованием понятий, фактов и методов математической науки. Следовательно, процесс ее решения является ничем иным, как процессом математического моделирования.
Современный образовательный процесс характеризуется сменой знаниево-ориентированной парадигмы на компетентностную. В этих условиях обострились проблемы и противоречия, связанные с математическим образованием. Среди них – противоречия между
– традиционными содержанием и методикой преподавания курса математики и потребностью в его практической и профессиональной ориентированности;
– преобладанием в курсе теоретических положений, их подробным, обремененным техническими деталями обоснованием, и необходимостью формирования у учащихся операциональных, практико-ориентированных умений;
– возрастанием в курсе «удельного веса» самостоятельной работы и недостаточным для этого уровнем мотивации учащихся и др.
В связи с указанными обстоятельствами приобретает особую актуальность проблема сближения в учебном процессе «теоретической» и «реальной» математики, решаемая средствами эффективного использования идей и методов математического моделирования. Целью настоящей работы является выстраивание концепции математического моделирования и инновационной содержательно-методической линии, «пронизывающей» весь курс математики. При этом, по нашему мнению, речь должна идти не только о реализации межпредметных связей, но и о внутрипредметном моделировании как способе «переноса» знаний, умений и навыков в смежные разделы курса математики.
Объектом нашего рассмотрения является процесс обучения математике в старшей школе и (отчасти) на начальной ступени бакалавриата, а предметом рассмотрения – формирование умений, навыков, и, в конечном счете, компетенции математического моделирования.
Мы исходим из предположения о том, что ознакомление учащихся с общей концепцией математического моделирования и решение задач на построение, анализ и интерпретацию математических моделей создаст предпосылки для развития мотивации учащихся к изучению математики и будет способствовать (в соответствии с требованиями ФГОС), достижению следующих результатов освоения основной образовательной программы:
– освоению учащимися межпредметных понятий и универсальных учебных действий;
– формированию представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления;
– формированию основ логического, алгоритмического и математического мышления.
Исходя из цели и гипотезы, сформулируем следующие задачи настоящей работы:
1. Адаптировать понятийный аппарат и концептуальные положения теории математического моделирования к процессу изучения математики в системе «школа-вуз».
2. Проанализировать существующие подходы к понятию компетенции/компетентности и сформулировать понятие компетенции математического моделирования.
3. Разработать паспорт формирования компетенции математического моделирования.
4. Обозначить содержательное наполнение основных компонент компетенции математического моделирования.
Теоретическая значимость работы, по нашему мнению, состоит в следующем:
– представлены имеющиеся теоретические подходы к понятию математической модели, выделены этапы процесса моделирования, используемые в решении учебных задач;
– приведена содержательная характеристика компетенции математического моделирования (знать/уметь/владеть), уровней и признаков ее проявления;
– введено и проанализировано понятие содержательно-методической линии математических моделей.
Практическая значимость работы нам видится следующей. Поскольку центральной идеей является положение о необходимости введения в школьном курсе основных понятий, связанных с математическим моделированием, то решение задач мы предлагаем осуществлять именно с точки зрения указанного положения, т.е. в тесной связи с этапами моделирования, схемой представления модели, интерпретацией результатов и др. Данный тезис иллюстрируется на материале конкретных задач.
Понятийный аппарат
Примеры моделей
Ознакомление учащихся с понятийно-категорийным аппаратом математического моделирования мы предлагаем предварить следующими соображениями.
На современном этапе развития науки моделирование служит основным инструментом исследователя, становится одним из главных источников информации о процессах, происходящих в природе и обществе, обнаружения и обоснования имеющихся в этих процессах закономерностей. С ситуациями моделирования мы постоянно встречаемся в практической деятельности, порой этого даже не осознавая. Так, например,
1) решая задания теста, учащийся моделирует для себя ситуацию реального ЕГЭ;
2) проводя учения, подразделения МЧС имитируют свои действия в условиях реальной катастрофы;
3) испытывая автомобиль на стенде, экспериментатор моделирует ситуацию движения автомобиля в различных режимах и в различных дорожных условиях;
4) проводя следственный эксперимент, следователь моделирует обстоятельства реального преступления;
5) летающая авиамодель в иных масштабах и в упрощенном виде моделирует полет настоящего воздушного судна;
6) географическая карта служит моделью реальной местности;
7) диаграмма на экране монитора служит моделью изменения курса валюты за определенный промежуток времени;
8) ЭКГ моделирует работу сердца в виде изображения ломаной линии в системе координат;
9) вычисление (по определенным правилам) вероятности события есть моделирование степени объективной возможности наступления данного события в умозрительном эксперименте;
10) количественные характеристики реально осуществленной выборки служат (с определенными оговорками) моделями тех же характеристик генеральной совокупности некоторых исследуемых объектов;
11) известные формулы прямо пропорциональной зависимости (закон равномерного движения S = vt, второй закон Ньютона, записанный в виде F = ma и др.) служат «символьными образами» реальных зависимостей.
Анализируя указанную информацию, можно увидеть разницу между примерами 1-5 и 6-11. В первом случае мы имеем реальное воспроизведение реальных же обстоятельств с теми же (аналогичными) участниками, но в иных условиях, на ином отрезке времени, в иных масштабах, и т.д. Во втором мы наблюдаем иной, нежели в реальных обстоятельствах, способ фиксации ситуации, использование иного «языка» и т.п. Такие примеры могут служить пропедевтическим материалом, предваряющим понятие идеальных, и, в частности, математических моделей (схемы, карты, чертежи, графики, символы, языки программирования и т.п.).
Различные подходы к понятию модели
Данное понятие (в частности, математическая модель), строго говоря, представляется первоначальным, неопределяемым понятием. Оно основывается на интуитивном представлении об изучаемом объекте, вводится его описание через другие понятия, также ранее не определенные (первоначальные).
Приведем имеющиеся в литературе (см., напр., работы [13, 18] и библиографию в них) формулировки (описания) понятия модели.
«Моделирование есть замещение некоторого объекта А другим объектом М. Замещаемый объект А называется оригиналом или объектом моделирования, а замещающий Б – моделью». Другими словами, модель – это объект-заменитель объекта-оригинала, обеспечивающий возможность изучения некоторых свойств оригинала.
«Модель есть намеренно упрощенная схема некоторой части реальной жизни, с помощью которой мы надеемся получить рекомендации к решению реальных проблем».
«Объект М является моделью объекта А относительно некоторой системы S характеристик, если М имитирует А по этим характеристикам».
«Модель есть искусственно созданный объект, который, будучи подобен исследуемому объекту (явлению), отображает и воспроизводит (в виде знаковых форм, формул, схем и т.п.) в более простом и огрубленном виде структуру, свойства, взаимосвязи и отношения между элементами данного объекта (явления)».
«Целью моделирования являются получение, обработка, представление и использование информации об объектах, которые взаимодействуют между собой и внешней средой; модель здесь выступает как средство познания свойств и закономерности поведения объекта. Модель представляет собой как бы проекцию объективной реальности под определенным углом зрения».
Общим для этих описаний является положение о том, что моделирование есть замещение одного объекта (оригинала) другим, который и будет называться моделью.
В настоящей работе мы будем придерживаться концепции А.А. Ляпунова (см. напр. [27]), согласно которой «моделирование есть опосредованное практическое или теоретическое исследование объекта, изучающее не сам объект, а некоторую вспомогательную искусственную или естественную систему (модель):
– находящуюся в некотором объективном соответствии с познаваемым объектом;
– способную замещать его в определенных отношениях;
– дающую при её исследовании, в конечном счете, информацию о самом моделируемом объекте».
Математическая модель: характеристики и этапы моделирования
С понятием модели и целями моделирования учащемуся на доступном уровне целесообразно познакомиться уже в курсе основной школы, при этом уровень строгости изложения должен соответствовать возрастной группе учащихся. Математическая модель «в первом приближении» должна ассоциироваться с неким необычным образом реального объекта или процесса, так что моделирование представляет собою путешествие в сказочную страну «Математика», где живут символы, формулы, графики, геометрические фигуры и др., в которые волшебным образом превратились предметы, связи, взаимоотношения, существующие в реальном мире. При этом задача учащегося – выполнить какие-либо действия и «разгадать», что кроется за итоговой формулой, тем или иным результатом, – словом, восстановить цепочку подлинных событий и фактов.
Ознакомление с «миром моделей» на более строгом уровне возможно в старшей школе. Здесь уже речь пойдет о записи свойств изучаемого объекта, процесса или явления на формальном языке с целью получения нового знания (обнаружения новых свойств) путем применения формальных же (математических) методов.
Согласно [22], под математическим моделированием понимается процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью; исследование этой модели, позволяет получать характеристики рассматриваемого реального объекта.
Будем рассматривать математическую модель как приближенное представление реальных объектов, процессов или систем, выраженное в математических терминах и сохраняющее существенные черты оригинала; при этом математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи. В частности, при моделировании физического процесса ему сопоставляется система математических соотношений, решение которой позволяет получить ответ на вопрос о поведении объекта без создания собственно физической модели.
Согласно концепции А.А. Ляпунова, процесс математического моделирования должен состоять из трех следующих основных этапов.
1. Прежде всего, строится так называемая содержательная модель в терминах исходной предметной области (иногда называемая также концептуальной моделью).
Концептуальная модель содержит исходную информацию для аналитика, выполняющего формализацию задачи и использующего для этого определенную методологию и технологию.
При построении содержательной модели формулируются так называемые постулаты модели (напр., гипотеза о линейном характере исследуемой зависимости), т.е. происходит переход к упрощенному, схематическому описанию объекта.
2. Следующий этап – перевод содержательной модели на формальный математический язык, т.е. переход к собственно математической модели.
3. Третий этап состоит в изучении математической модели, т.е. решении полученной математической задачи.
4. Последним является этап интерпретации (истолкования) результата исследования математической модели, следствием чего будет получение новой для исследователя информации о свойствах реального объекта (для чего, собственно, и был нужен весь процесс моделирования).
Первые два «предматематических» этапа наиболее важны с точки зрения создания модели, адекватной исходному процессу (явлению). По А.А. Ляпупову [27], здесь имеются свои шаги (ступени).
Шаг первый состоит в наблюдении, сборе, коллекционировании материалов.
Шаг второй – «систематизация, инвентаризация, индексирование, поиск системы».
Шаг третий – выдвижение гипотезы, ее проверка, проведение эксперимента.
Шаг четвертый – построение теории или соответствующий феноменологической модели изучаемого явления (модель в первом приближении; модель в статусе временного, подлежащего уточнению решения; ситуация типа «ведем себя так, как если бы…»).
И лишь пятый шаг, как высшая точка процесса, – математическое описание объекта, явления, системы.
Вернемся к этапам моделирования. Третий этап, собственно математический, определяется характером возникающей математической задачи и имеющимися средствами ее решения. Здесь мы выделяем следующие шаги.
Шаг 1. Выбор носителя модели, т.е. той математической теории, на базе которой будет решаться математическая задача.
Шаг 2. Выбор метода решения: аналитический (если он принципиально возможен или если уровень развития теории позволяет его осуществить), либо численный.
Шаг 3. Разработка алгоритма решения (так, для краевой задачи математической физики такой алгоритм заложен в методе Фурье; при численном решении речь может идти о блок-схеме и т.д.).
Шаг 4. Реализация алгоритма. Получение результата.
Наиболее часто здесь возникают уравнения различного характера, неравенства, системы уравнений или (и) неравенств, задачи максимизации (минимизации), оптимизации, и др.
Наконец, четвертый этап – это этап возвращения к исходной предметной области. Именно на этом этапе мы получаем требуемую информацию об исходном процессе (явлении), которую мы не могли получить другими средствами. В частности, если речь идет о процессе, то возникает возможность
– определить состояние процесса в определенные моменты времени, промежуточные между теми, в которые это состояние уже было известно;
– прогнозировать состояние процесса за рамками данного временного интервала.
Первая возможность называется интерполяцией, вторая – экстраполяцией.
Подводя итог, цель математического моделирования мы усматриваем в создании и реализации математического аппарата, позволяющего умозрительно обнаружить связи между теми или иными процессами, явлениями, факторами, и предвидеть конечный результат их действия. Математическая модель по мере накопления фактов перерастает в математическую теорию, которая сама начинает служить источником информации.
Схема представления модели
Полезно ознакомить учащихся со следующей общей схемой представления модели: X > W > Y. Здесь X – вектор входных переменных, Y – вектор выходных переменных (исходы модели); W – так называемый оператор модели, обеспечивающий преобразование информации (X преобразуется в Y) в соответствие с задачей, решаемой на модели. Имеются следующие три варианта упомянутых задач:
1) прямая задача: известны Х и W, необходимо найти Y;
2) обратная задача 1: известны Y и W, необходимо найти X;
3) обратная задача 2: известны X и Y, необходимо найти W.
В последней задаче случае возможны случаи «черного ящика» – оператор модели полностью неизвестен, и «серого ящика» – при известной структуре оператора неизвестны значения параметров.
Так, например, в учебных задачах, относящихся к моделированию физических процессов, в качестве вектора входных переменных Х обычно выбирается набор физических характеристик объектов, подверженных, например, механическим колебаниям (струна, стержень), совокупность теплофизических характеристик материалов, в которых происходит теплообмен; в задачах экономики вектор Х определяется набором исходных данных, подлежащих анализу (объем выпускаемой продукции, цены, показатели спроса и др.) и т.д. В основе построения оператора модели лежит некоторый физический закон, закономерности рынка [1, 3] и т.п. Получаемый результат (число или набор чисел, функция или совокупность функций, функциональный ряд и др.) и порождает компоненты вектора Y выходных переменных.
Здесь следует подчеркнуть, что поиск оператора модели во многих случаях есть составная часть процесса моделирования.
Понятие системы. Системный подход
В общих чертах учащиеся должны иметь представление о математическом моделировании систем и системном подходе. Принцип системности – это философский принцип, выполняющий как мировоззренческие, так и методологические функции. Учащихся, по нашему мнению, следует ознакомить с наиболее употребимыми в литературе определениями (см., напр., [2, 4, 22]) и библиографию в них).
Система – в «первом приближении» – есть совокупность взаимодействующих, взаимосвязанных элементов.
Расширение понятия может быть следующим: система понимается как общенаучная категория для обозначения явлений естественного или искусственного мира, имеющих внутреннюю целостность, завершенную структуру и функциональное назначение.
Дальнейшее расширение и уточнение: системой называют совокупность элементов, взаимосвязанных между собой таким образом, что возникает определенная целостность, единство; указанная целостность обладает новыми интегративными свойствами, отсутствующими у каждого из элементов (эмерджентные свойства).
Интеграция рассматривается как процесс и результат создания неразрывно связанного, единого, цельного. В соответствии с концепцией В.А. Энгельгардта [30], следует говорить о следующих трех стадиях интеграции:
а) возникновение системы связей между частями;
б) утрата (возможно неполная) частями некоторых своих первоначальных идентификационных качеств при вхождении в состав целого;
в) появление у возникающей целостности новых свойств, обусловленных как свойствами частей, так и возникновением новых систем межчастных связей.
Наличие эмерджентных свойств именуется также синергией. Учащийся должен понимать, что именно синергия отличает систему от простого соединения (синтеза) некоторых элементов. В синергии проявляется суммирующий эффект взаимодействия нескольких факторов, характеризующийся тем, что их действие существенно превосходит эффект каждого отдельного компонента в виде их простой суммы.
Наиболее наглядно синергия проявляется в жизнедеятельности живых организмов, которая сама возможно лишь в результате взаимодействия процессов и явлений, протекающих в организме. Примером синергии в в физике может служить результат соединения двух и более частей радиоактивного материала, которое, с превышением критической массы, порождает выделение энергии в количестве, превышающем суммарное излучение энергии отдельных частей. В общественной жизни знания и усилия социума превосходит суммарные знания и усилия индивидов. В экономике эффектом слияния компаний может быть получение прибыли, превосходящей суммарную прибыль, имевшуюся до их слияния.
Наконец, учащийся должен иметь первоначальное представление о системном подходе: данный подход есть направление о методологии научного познания, в основе которого лежит рассмотрение объекта как системы [12]. Математическое моделирование является важнейшим компонентом данной методологии, поскольку построение математической модели как раз и призвано (в математической же форме) отразить наиболее важные, существенные связи между элементами моделируемых систем. Удачно построенная и исследованная модель в процессе её интерпретации позволяет выявить в числе свойств системы также наличие синергии.
Иерархия моделей. Свойство универсальности
Решение практических или прикладных задач часто сопровождается некоторой идеализацией реального объекта или ситуации, пренебрежением малозначительными факторами. Учащийся должен понимать, что при этом необходимо соблюдать разумный баланс между адекватностью модели и ее простотой. Адекватность выступает здесь как требование воспроизведения моделью с достаточной полнотой и точностью всех свойств системы, существенных для целей данного исследования; сложность модели не должна превосходить некоторого предела, определяемого возможностями математического аппарата, которым располагает исследователь. На практике часто исследователь строит последовательность моделей, получающихся одна из другой путем последовательного же отказа от предположений, идеализирующих изучаемую систему. Таким образом, выстраивается иерархическая цепочка математических моделей, уточняющих и обобщающих одна другую. Ясно, что при этом утрачивается простота и растет степень адекватности моделей.
Учащимся школы достаточно иметь лишь общие представления об иерархии моделей. Студенту вуза уже доступно изучение иерархических цепочек моделей многих объектов и процессов, относящихся к их будущей профессиональной деятельности. Например, речь может идти о процессе тепломассопереноса. В простейшем случае рассматривается процесс распространения тепла в стержне при отсутствии источников и поглотителей тепла, и с поддержанием нулевой температуры на его концах. При этом решается однородное уравнение в частных производных с однородными краевыми условиями. Усложнение модели происходит, когда температура на концах стержня может меняться с течением времени. Наконец, отказ от предположения «свободного» теплообмена (т.е. присутствие источников или поглотителей тепла) приводит к так называемой неоднородной (существенно более сложной) краевой задаче.
При достаточно глубоко разработанном математическом аппарате возможен и другой путь изучения моделей: «от общего к частному» [20]. А именно, исследователь рассматривает и решает математическую задачу в общем виде. Затем, опираясь на соответствующую «общую» модель, путем последовательных рассмотрений частных случаев, он выстраивает цепочку более простых моделей. Данный подход позволяет, установив общие свойства системы, конкретизировать и дополнить их в частных случаях.
Свойство универсальности математических моделей проявляется в возможности применения одной и той же модели к объектам (системам) принципиально различной природы, подчиняющимся разным фундаментальным законам. Универсальность математических моделей объясняется, с одной стороны, как единством проявления физических свойств окружающего мира, так и абстрактностью математических теорий, их отвлеченностью от объекта исследования с другой стороны. «Математика – это искусство давать разным вещам одно наименование» [19].
Примером простейшей универсальной математической модели является функциональная зависимость у = k х. При соответствующем «наполнении» данное уравнение может описывать совершенно разные закономерности (закон равномерного прямолинейного движения при постоянной скорости, размер уплачиваемого налога при постоянном проценте отчисления и др.).
Другим примером служит линейное дифференциальное уравнение второго порядка x» = – 2x с постоянным коэффициентом – 2, описывающее процесс (процессную систему) свободных механических колебаний и электромагнитных колебаний. В приведенных и других примерах универсальных математических моделей (см., напр., [10, 11]) одним и тем же символам следует дать соответствующую данной системе интерпретацию. Таким образом, в универсальности математических моделей проявляется интегрирующая роль математики и ее методов.
Математическое моделирование при решении учебных задач
Обсудим, как реализуется четырехэтапный процесс математического моделирования применительно к учебным задачам.
Трансформация содержательной модели в модель математическую
Как правило, в учебных задачах содержательная модель уже представлена в условии задачи. Остается только ее проанализировать и формализовать.
На этапе трансформации содержательной модели в модель математическую мы выделяем два возможных уровня сложности решаемых задач. Первый уровень соответствует уже данной знаковой модели, и тогда остается завершить переход к задаче математической: уточнить постановку, выявить дополнительные условия (ограничения на параметры, начальные или краевые условия и т.п.). Такими являются, например, «задачи с прикладным содержанием» банка контрольно-измерительных материалах ЕГЭ. В значительно большей степени интеграция знаний проявляет себя в случае второго уровня сложности, когда саму знаковую модель предстоит еще построить, на основе, например, вербального описания процесса.
Особенности некоторых моделей
1) Моделирование ситуаций аналитически заданными функциями, уравнениями и их системами. Таковыми являются, например, ситуации, описываемые в задачах на составление уравнений. Здесь происходит переход от вербальной модели к математической, при этом построение математической модели есть, по сути, построение ее оператора на основе зависимостей (законов), представленных в условии задачи. Так, например, уравнение вида f(x) = b или система уравнений вида f(x, y) = p, g(x, y) = q может быть истолкована как информация о выходных значениях (b и (p, q), соответственно) оператора. представленного функциями f и g. Используя эту информацию, следует определить «входные» значения х и у (см. обратную задачу № 1 математического моделирования в п. 1.4.).
2) Интерполяция и экстраполяция позволяют отыскивать аналитические зависимости, близкие к функциям, описывающим реальные закономерности. Так, например, при моделировании состояний систем, меняющихся во времени, на заданном временном интервале [1, 2] в некоторые фиксированные моменты t1, t2,…, tn наблюдаются значения функции f(t1), f(t2),…, f(tn). Требуется восстановить значения f в другие моменты. Если из каких-либо соображений известен вид функции f(t; a1,…, am), где a1,…, am – неизвестные параметры, то эти параметры могут быть определены из условия совпадения значений функции f в точках tk с данными наблюдений. Соответствующий способ аппроксимации функции и нахождения «промежуточных» значений и является интерполяцией. Ясно, что для вычисления параметров функции необходимо определенное число наблюдений (измерений) в зависимости от вида искомой функции. Так, для определения коэффициентов многочлена n-ой степени необходимо n + 1 наблюдений.
Процесс аппроксимации функции и вычисления её значений за пределами интервала [1, 2] наблюдения представляет собою экстраполяцию. В более широком понимании, всякое научное представление, порожденное математической моделью, есть экстраполяция (с наблюдаемых ситуаций на ненаблюдаемые, с измеренных величин на неизмеренные и т.д.). Расширение понятия экстраполяции на общий случай существования и перспектив развития системы в будущем называется прогнозированием.
Задачи интерполяции и экстраполяции связаны с обратной задачей 2 моделирования, т.е. с поиском оператора W модели. Случай известного вида искомой функции (напр., многочлена) относится к ситуации «серого ящика».
3) «Внутриматематическое» моделирование. Примерами могут служить «алгебраические» способы решения геометрических задач. Так, исходя из теорем и формул геометрии, задача ттрансформируется в уравнение относительно искомой величины или систему уравнений относительно величин, среди которых присутствуют и искомые.
4) Особым случаем моделирования является математическое моделирование стохастических процессов, активно внедряющееся в настоящее время в курс математики средней и даже начальной школ (см., напр., [6]).
Примеры построения математических моделей
1) Задача интерполяции и экстраполяции. В начале месяца электросчетчик показывал 1050 (квт.), а 20-го числа 2000 (квт.). Считая, что рост потребленной электроэнергии равномерным, определить показания счетчика 5-го числа. Каково должно быть показание счетчика в конце месяца (30-го числа), если потребление электроэнергии будет оставаться равномерным?
Здесь имеется вербальное представление ситуации. Для построения математической модели (нахождения оператора модели) следует знать, что равномерно протекающие процессы описываются линейными функциями. Следовательно, искомая зависимость имеет вид y = kt + b («серый ящик»). Значения t = 0 и t = 5 можно считать «входными», а y = 1600 и y = 2000 – «выходными». Параметры k и b искомой линейной зависимости определяются теперь как решения соответствующей системы уравнений. «Восстановленный» оператор есть зависимость вида y = 20t + 1600. Теперь возможно нахождение потребленной электроэнергии в любые промежуточные дни и дни после 20-го числа данного месяца (получение этой информации можно отнести к этапу интерпретации модели).
2) Приведём задачу моделирования физического процесса из открытого банка контрольно- измерительных материалах ЕГЭ (www.mathege.ru). В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону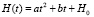 
, где H0 = 6,25 м. – начальный уровень воды, 
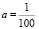м/мин2, и 
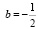м/мин – постоянные, t – время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? (Ответ приведите в минутах).
Данную ситуацию можно отнести к первому уровню сложности моделирования: знаковая модель уже представлена в условии задачи, требуется лишь уточнение модели, т.е. сведение задачи к поиску промежутка решений неравенства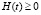 
.
3 В случае того же физического процесса рассмотрим задачу моделирования второго уровня сложности (см. [15]). Из цилиндрического резервуара (площадь основания которого равна S, а высота равна H), заполненного жидкостью, через отверстие площадью s в его дне начинает вытекать жидкость со скоростью, пропорциональной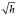 
, где h – высота жидкости над отверстием; коэффициент пропорциональности k известен. Через сколько времени вся жидкость вытечет из резервуара?
На первом этапе решения требуется построить знаковую модель (формализация задачи), для чего применяем следующие рассуждения. Объем жидкости V, вылившейся за промежуток времени t, равен произведению – Sh, где h – изменение высоты h жидкости над отверстием; очевидно, что высота жидкости убывает, так что h < 0, чем и объясняется появление знака «минус» в записи произведения. С другой стороны, этот же объем равен sl, где l – высота вылившейся (через отверстие площадью s) цилиндрической струйки, при этом l (путь, проделанный жидкостью) приближенно равен vt, поскольку можно считать истечение жидкости за малые промежутки времени t практически равномерным. Сравнивая полученные двумя способами значения выражения для объема V вытекшей жидкости, получим
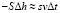
или, согласно условию (пропорциональность скорости величине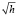 
),
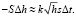
При стремлении к нулю приращения t последнее приближенное равенство становится все более точным и может быть заменено равенством соответствующих дифференциалов (взятых с постоянными коэффициентами)
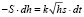
или
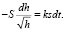
Решая полученное дифференциальное уравнение (этап исследования модели), и учитывая, что в начальный момент резервуар был заполнен (т.е.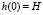 
), получаем
.
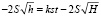Теперь возможна интерпретация модели. Резервуар опустеет в тот момент, когда h = 0. В этом случае получаем
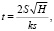
что и служит ответом задачи.
4) Приведем пример задачи оптимизации, решаемой средствами дифференциального исчисления. Требуется позолотить ларец формы прямоугольного параллелепипеда (стенки и крышку) объема 72 куб. ед., у которого длина основания вдвое больше его ширины. При каких размерах ларца будет потрачено меньше всего позолоты.
Компетенция математического моделирования
Компетенции: основные понятия
Понятие компетенции/компетентности в современной педагогической науке не является устоявшимся. Поэтому обсудим имеющиеся здесь подходы. В литературе (см. напр., [5, 7, 28, 29]) компетенция определяется как
– способность и готовность личности к той или иной деятельности;
– способность (умение) мобилизовать в данной ситуации полученные знания и опыт;
– способность к осуществлению реального жизненного действия;
– возможность эффективно действовать за пределами штатных (учебных) ситуаций;
– инструмент, с помощью которого можно осуществлять различные действия, оказываться подготовленным к новым ситуациям.
Общим для указанных и других определений представляется понимание компетенции как
– способность личности справляться с самыми различными задачами;
– обладание знанием и опытом, позволяющими ей быть успешной в собственной жизнедеятельности;
– умение осуществлять выбор, исходя из адекватной оценки своих возможностей в конкретной ситуации, актуализировать и применять в этой ситуации имеющиеся знания и опыт.
Безусловно, анализ общих моментов и принципиальных различий в приведенных (и других) подходах к пониманию компетенции представляет определенный теоретический интерес, однако, с практической точки зрения достаточно ограничиться рабочим представлением о компетенции как о способности (возможности) устанавливать связь между знанием, умением, навыком (ЗУН) и ситуацией, сформировать процедуру решения проблемы.
Компетентностный подход приобрел особую значимость в в связи с так называемым Болонским процессом и нашел свое отражение в программных документах «Концепция модернизации российского образования на период до 2010 года» ([8]) и «Стратегии модернизации содержания образования» ([23]).
И хотя соответствующие идеи можно было обнаружить в работах советских и российских педагогов В.В. Краевского, И.Я. Лернера и др., практическая реализация компетентностного подхода началась в странах Западной Европы и Америке (competence-based education – СВЕ) с конца 60-х годов – периода наиболее активного реформирования систем образования.
Тогда же возникла одна из точек зрения на различие между понятиями «компетенция» и «компетентность», где последнему отводилась роль основанного на знаниях интеллектуально и личностно обусловленного опыта социально-профессиональной жизнедеятельности человека ([7]).
Следует отметить, разрабатываемые в России понятия компетенций имеют (в сравнении с европейским и американским вариантами) существенное различие в их содержательной части ([5]).
В западном варианте преобладает прагматический аспект: «основные характеристики людей», которые «причинно связаны с эффективным выполнением работы», и «проявляются в различных ситуациях, в течение длительного периода времени» и которые могут быть измерены или подсчитана с целью дифференцировать «превосходных» и «средних», или эффективных и неэффективных исполнителей; основной акцент делается на способность демонстрировать работу, соответствующую стандартам.
Отечественный же вариант компетентностного подхода имеет ярко выраженный рефлексивный аспект, выраженный в осмыслении своих собственных действий и их законов. Так, в процессе обучения, где и формируются компетенции, по мнению Е.В. Доманского [5], компетентностный подход может запустить механизмы самоактуализации обучения, самоопределения учащегося, освоения своего физического, интеллектуального и духовного развития. С введением компетентностного подхода «образование сделало шаг в сторону понимания того, что основные перемены должны происходить не вне, а внутри учащегося».
Образовательные компетенции
Связывая процесс формирования компетенций с образовательным процессом, А.В. Хуторской [29] вводит понятие образовательной компетенции, определяя ее как «отчужденное, наперед заданное требование к образовательной подготовке учащихся» (в соответствии с государственным заказом, стандартом). «Образовательные компетенции… моделируют деятельность ученика для его полноценной жизни в будущем ». Образовательная компетенция предполагает усвоение не отдельных друг от друга знаний и умений, а овладение комплексной процедурой, в которой для каждого выделенного направления присутствует соответствующая совокупность образовательных компонентов, имеющих личностно-деятельностный характер.
Само определение образовательных компетенций предполагает, что они базируются на ЗУНах, однако никакая компетенция не сводится лишь к этой триаде: ее можно рассматривать как некоторую сферу отношений между знаниями, умениями, навыками формирующейся личности и ее действием в социальной практике. Компетенция предполагает одновременную мобилизацию знаний, умений и способов поведения в условиях конкретной деятельности.
В результате формирования образовательной компетенции учащийся приобретает возможность «переносить знания», решать новые для себя задачи, осваивать новые предметные области, новые виды деятельности и т.п. Следовательно, можно говорить о возникновении свойств эмерджентности и рассматривать компетенцию как систему.
Как следует из выводов цитированных выше авторов, совокупность компонентами всякой образовательной компетенции являются:
– ценностно-смысловые ориентации (компоненты внутреннего мира личности, представляющие собой индивидуальное преломление общественных ценностей, убеждение учащегося в желательности достижения тех или иных целей, включение их в личностный смысловой контекст);
– кругозор (наличие представлений о предмете, процессе, явлении, его характерных признаках, умение привести соответствующий пример и контрпример);
– знание (в общем случае – результат познания, отраженный в сознании человека в виде совокупности понятий, теоретических построений и представлений, проверенных практикой и удостоверенных логикой; в учебном процессе – понятое и усвоенное содержание предмета, процесса, явления, способность дать соответствующие данному знанию определения через структуру и связи с другими понятиями);
– умение (овладение новым способом действия в процессе решения определенного класса задач, основанное на каком-либо знании);
– навык (доведенные до автоматизма умения решать определенные типы задач, способность к действию, достигшему наивысшего уровня сформированности, совершаемому без осознания промежуточных шагов);
– опыт деятельности (совокупность практических знаний, умений, навыков, приобретаемых в ходе повседневной деятельности, внутренний результат этой деятельности);
– личностные качества, рефлексия (личностные характеристики, необходимые для наиболее эффективной работы в определенной ситуации, процесс осознания субъектом образования собственной деятельности, критическая самооценка, познание своих возможностей).
Понятие компетенции математического моделирования
Компетенция математического моделирования введена в педагогическую науку сравнительно недавно (см. напр., [21]). Применительно к системе «школа-вуз», данную компетенцию можно определить как способность актуализировать и применять математические знания и умения при построении, анализе и интерпретации математических моделей в процессе решения задач как учебных, так и практических.
Согласно приведенной выше структуре образовательной компетенции, выделим следующие компоненты компетенции математического моделирования.
1) Мотивационно-ценностное отношение к математическим знаниям и умению строить математические модели в процессе учебной и практической деятельности. Росту мотивации, как подчёркивалось выше, способствуют понимание универсальности математического языка, знакомство со свойством универсальности ряда математических моделей. Изучая «смежные» дисциплины и, одновременно, будучи знакомым с понятиями, этапами и методами математического моделирования, учащийся должен прийти к убеждению, что математические методы могут выступать в качестве инструмента исследований в различных областях деятельности, в силу чего освоение математических дисциплин становится осознанной целью и подлежит включению в личностный смысловой контекст деятельности учащегося.
2) Кругозор и постоянное его расширение – необходимый компонент в компетенции математического моделирования. Речь идет не только об освоении содержания учебных дисциплин, но и постоянном росте культурного уровня учащегося. Интерес ко всему происходящему в мире в настоящее время, к истории, к отечественной и зарубежной культуре, литературе, искусству неизбежно сопровождается анализом явлений и процессов, сравнительными характеристиками, логическими умозаключениями и т.п. В свою очередь, указанные формы мыслительной деятельности способствуют развитию умений выделять главное и отбрасывать второстепенное, кратко и ясно выражать свои мысли, ставить задачи, получать и четко формулировать выводы, а эти умения успешно «встраиваются» в процессы математического моделирования.
3) Знания и умения как в области математики, так и в «исходных» предметных областях являются наиболее существенными компонентами данной компетенции. В первую очередь, речь идет об умении актуализировать математические знания применительно к выстраиваемой модели в условиях конкретной ситуации. Владение методом математического моделирования предполагает развитие целого комплекса умений:
– умение решать задачи (постановка вопроса, нахождение нужной информации для решения задачи, анализ проблемной ситуации, выдвижение гипотезы);
– способность к математизации объектов и процессов (определение данных, условий и границ поиска решений, перевод проблемы на язык математики, применение адекватного математического аппарата);
– умение логически мыслить (дедуктивные и индуктивные умозаключения, комбинация логики и интуиции, аргументация выводов и заключений);
– коммуникативные умения (чтение, письмо, речь на языке математики, использование математических символов и формул, построение графиков, схем, диаграмм);
– умение применять современные информационные технологии.
4) Опыт математической деятельности, в том числе, и в области математического моделирования, способствует закреплению умений в форме навыков. На основе опыта, приобретенного в процессе решения учебных задач, возникает и развивается способность к переносу математических знаний и умений на незнакомые ситуации, в том числе, возникающие в практической деятельности.
5) Наконец, рефлексия как самооценка деятельности в области математического моделирования способствует развитию таких качеств учащегося, как самоконтроль, ответственность, рациональность, самостоятельность.
Паспорт формирования компетенции математического моделирования
Для уточнения результатов освоения компетенции математического моделирования в терминах «знать/уметь/владеть» будем использовать так называемый паспорт компетенции. Он включает в себя:
– место и значимость компетенции в соответствии с требованиями Федерального государственного стандарта к уровню сформированности компетенции по окончании освоения образовательной программы (ООП);
– уточнение компонент содержания компетенции;
– структурирование компетенции на уровни, показатели и дескрипторы.
Формирование компетенции математического моделирования в совокупном ожидаемом результате образования выпускника школы способствует подготовке выпускника к выполнению следующих видов учебной и практической деятельности:
– анализ понятий, фактов, ситуаций из различных предметных областей с использованием логических выводов, математического языка и методов математики и получение, вследствие этого, необходимой информации в рамках соответствующей предметной области;
– интерполяция и экстраполяция результатов;
-прогнозирование поведения процессов средствами вероятностно-статистической теории;
– получение, в конечном счете, практических рекомендаций при решении прикладных задач.
Уточненные компоненты содержания компетенции:
– предметный – теоретическая основа компетенции математического моделирования, включающая в себя математические знания и умения, а также соответствующие способы действия: использование методов математической логики, геометрии, алгебры, математического анализа и стохастики;
– собственно модельный, предусматривающий осуществление вышеназванных этапов процесса моделирования;
– вычислительный – решение задач в общем виде и с конкретными числовыми значениями величин, предполагающее знание правил и методов вычислений;
– прогностический – направленный на выяснение тенденций развития состояний исследуемого явления или объекта.
Результаты обучения, раскрывающие структуру компетенции и планируемые уровни ее сформированности
Мы выделяем три следующих основных уровня.
1) Пороговый уровень, как минимально необходимый для всех выпускников старшей школы по завершении освоения ООП; на этом уровне предполагается овладение минимальной системой знаний, умений, навыков (ЗУН), что бывает достаточным для анализа простейших математических моделей. Работа с более сложными моделями может осуществляться под руководством преподавателя.
2) Базовый уровень, позволяющий работать с типовыми задачами, использовать известные алгоритмы, правила и методы как в решении собственно математических задач, так и на этапах математического моделирования. Речь идет, по сути, о соответствии требованиям к результатам освоения ООП среднего (полного) общего образования в области математики на базовом уровне.
3) Продвинутый уровень – максимально возможная выраженность компетенции, которая важна как качественный ориентир для самосовершенствования. Здесь речь идет о соответствии требованиям к результатам освоения ООП среднего (полного) общего образования в области математики на профильном и углубленном уровнях.
Перечислим основные (по нашему мнению) признаки каждого из перечисленных уровней (знать/уметь/владеть).
На пороговом уровне учащемуся необходимо
– знать: основные формулы алгебры и тригонометрии, определения и графики основных элементарных функций, формулировки понятий и фактов геометрии, необходимых для решения простейших планиметрических и стереометрических задач, методы исследования функциональных зависимостей, элементарные положения теории вероятностей и математической статистики;
– уметь: выполнять стандартные алгебраические и тригонометрические преобразования и решать простейшие алгебраические и трансцендентные уравнения, выполнять построение на плоскости изображений плоских или пространственных геометрических объектов, вычислять производные и интегралы на основе табличных формул, извлекать информацию, представленную в таблицах, на диаграммах, графиках;
– владеть: методами геометрической интерпретации простейших задач на определение взаимного расположения объектов, нахождения их размеров и числовых характеристик (площади, объемы), методами дифференциального исчисления в простейших случаях исследования моделей (например, вычисление скорости, ускорения и т.п.), способами систематизации статистических данных в виде рядов распределения, полигонов и гистограмм.
На базовом уровне учащийся должен
– знать: в полном объеме изучаемые в школьном курсе математики формулы алгебры и тригонометрии, функциональные понятия и их графические интерпретации, понятия и факты геометрии, основные положения дифференциально-интегрального исчисления, основные вероятностные схемы и формулы теории случайных событий, а также понятия и факты, связанные с анализом эмпирических распределений;
– уметь: проводить доказательства основных известных (из школьного курса) математических утверждений, выполнять основные шаги алгоритма математического моделирования, использовать функционально-графические представления для решения как математических, так и практико-ориентированных задач, использовать факты геометрии для описания предметов окружающего мира, описывать и анализировать массивы числовых данных с помощью подходящих статистических характеристик, использовать понимание вероятностных свойств окружающих явлений при принятии решений;
– владеть: навыками устных, письменных, инструментальных вычислений при решении практических задач, символьным языком алгебры, тригонометрии, геометрии и его использованием при формализации задач из смежных областей и практико-ориентированных задач; необходимыми для решения приёмами выполнения преобразований, нахождения корней уравнений и др.; системой функциональных понятий и фактов для описания и анализа реальных зависимостей; способами представления и анализа статистических данных; способами изучения статистических закономерностей в реальном мире; способами построения и изучения простейших вероятностных моделей.
На продвинутом уровне предполагается, что учащийся, в дополнение к знаниям, освоенным на базовом уровне, обладает первичными знаниями аналитической геометрии, комплексного анализа, теории многочленов, дифференциальных уравнений, а также умеет комбинировать известные ему методы доказательств при обосновании новых утверждений, переносить освоенные приемы решения задач на новые, в том числе, практические ситуации.
Продвинутый уровень предполагает, что учащийся владеет:
– специальными приемами решения задач повышенной сложности (напр., задач с параметрами и др.);
– векторно-координатным методом (в дополнение к стандартным геометрическим методам) анализа расположений объектов на плоскости и в пространстве;
– расширенным алгоритмом исследования функциональных зависимостей (включая асимптотическое поведение функций, характер выпуклости и др.) и специальными приемами интегрирования отдельных классов функций;
– стандартными распределениями случайных величин и методами получения точечных и интервальных оценок параметров теоретических распределений.
Содержательно-методическая линия математических моделей
Типы моделей
Мы выделяем четыре основных типа моделей, возникающих при решении учебных задач.
1) Модели логического типа: здесь имеет место формализация рассуждений средствами операций над высказываниями и предикатами. Носителем модели является, соответственно, алгебра высказываний или логика предикатов.
2) Аналитические модели: здесь процессы функционирования реальных объектов, или систем записываются в виде явных функциональных зависимостей. Эти модели разделяется на классы в зависимости от математической проблемы:
– преобразования (нахождение образа при действии некоторого оператора);
– уравнения (алгебраические, трансцендентные, дифференциальные, интегральные) и неравенства;
– аппроксимационные задачи (задачи интерполяция, экстраполяция, численные методы дифференцирования, интегрирования, решения дифференциальных уравнений);
- задачи оптимизации (например, задача линейного программирования).
3) Геометрические модели, носителями в которых являются факты и методы геометрии, а объектами исследования – плоские фигуры, поверхности, многогранники, тела вращения и т.д.
4) Модели стохастического типа (анализ данных, статистическая обработка результатов наблюдения, вероятностные характеристики случайных событий); см. напр., [6].
5) Модели смешанного типа. Так, например, задачи, решаемые средствами аналитической или дифференциальной геометрии используют как аналитический, так и геометрический аппарат; стохастические задачи, решаемые на основе действий над случайными событиями, используют свойства элементов булевых алгебр, общих как для алгебры событий, так и для алгебр множеств и высказываний [14].
Математический анализ как средство моделирования процессов и явлений
В качестве примера рассмотрим возможности средств математического анализа в решении проблем построения аналитических моделей.
Необходимость овладения учащимися элементами математического анализа обусловлена рядом требований, предъявляемых Федеральными государственными образовательными стандартами к результатам освоения основных образовательных программ [16, 25].
В частности, изучение элементов математического анализа способствует овладению системой функциональных понятий, развитию умения использовать функционально-графические представления для решения различных математических задач, для описания и анализа реальных зависимостей. Если функцию одной или нескольких переменных рассматривать как математическую модель реального процесса, то выстраиваются следующие связи понятий.
Таким образом, построение, анализ и интерпретация математических моделей процессов и явлений, требует освоения учащимися основ дифференциально-интегрального исчисления.
Связи характеристик процесса и функциональных понятий
|
Характеристики процесса |
Функциональные понятия |
|
Тенденции процесса, проявляющаяся с течением времени. |
Предел функции на бесконечности, асимптотическое поведение. |
|
Бесперебойное течение процесса (перепады, сбои). |
Непрерывность функции (разрывы). |
|
Скорость течения процесса. |
Производная функции. |
|
Изменение состояний в малые промежутки времени. |
Дифференциал функции. |
|
Рост, падение. |
Монотонность функции. |
|
Пиковые состояния (апогей, перигей). |
Экстремумы функции (наибольшее, наименьшее значения). |
|
Воспроизводимость состояний процесса. |
Периодичность функции. |
|
Промежуточные состояния. |
Интерполяция. |
|
Прогнозируемые состояния. |
Экстраполяция. |
|
Восстановление процесса по скорости его течения. |
Неопределенное интегрирование. |
|
Изменение процесса на временном промежутке, локально зависящего от времени протекания линейным образом. |
Определенный интеграл. |
Линия математических моделей
В каждой учебной дисциплине присутствуют фундаментальные понятия, вокруг которых группируется некоторое содержание (другие понятия, связанные с базовым, суждения и действия, необходимые для их усвоения и т.д.); при этом с каждым новым обращением учащихся к этим понятиям происходит обогащение представлений о них. Соответствующий блок содержания представляет собой некое целостное образование с многочисленными внутренними связями, с использованием специальных методов и определяет специфику методики изучения материала.
В подобных случаях говорят об определенной содержательно – методической линии в программе изучения данной дисциплины.
Линию математических моделей следует выстраивать в соответствии с уровнями образования. Так, на начальном уровне [6] решаются простейшие задачи, связанные практическими ситуациями, возникающими в жизни учащегося (стоимость покупки комплекта канцелярских изделий, систематизация данных о температуре воздуха в течение месяца, вычисление площади квартиры, сумма удержанного подоходного налога и др.).
В основной школе математические модели могут быть представлены традиционными задачами на составление уравнений (проценты, равномерное движение, работа, смеси-сплавы и др.), геометрическими задачами прикладного характера, формализованными задачами из физики и др. предметных областей. Здесь также присутствуют систематическое моделирование комбинаторных ситуаций (использование комбинаторных формул), вероятностное моделирование случайных событий, простейший анализ выборок.
В старшей школе учащийся владеет уже достаточно обширным арсеналом математических методов. В силу этого обстоятельства задачи на составление уравнений могут быть дополнены сложными задачами «финансовой математики» (группа заданий высокого уровня сложности из открытого сегмента контрольно-измерительных материалов ЕГЭ), задачами оптимизации и др. Полезно рассмотрение моделей, требующих использования интеграции методов (например, геометрических, тригонометрических, и алгебраических: геометрические задачи, моделируемые в виде систем уравнений; геометрических и аналитических: нахождение наибольших площадей, объемов и др.). При изучении математики на профильном уровне возможно конструирование и преподавание элективных курсов: «Математика в экономике», «Дифференциальные уравнения и их приложения», «Элементы математической статистики» и др.
Обсудим, как может быть представлена линия математических моделей в курсе математики бакалавриата инженерных направлений. С нашей точки зрения здесь следует выделить следующие модули.
1) Элементы математической логики и теории алгоритмов (данный модуль является интегрированным по отношению к курсам математики и информатики).
2) Линейная алгебра и аналитическая геометрия (средство моделирования экономических задач, задач оптимизации).
3) Дифференциально-интегральное исчисление (задачи геометрии, механики, электростатики, электродинамики, экономики и др.).
4) Векторный анализ (гидравлика, электродинамика, теплофизика и др.).
5) Обыкновенные дифференциальные уравнения (задачи сопромата, модели «естественного роста», «процессов выравнивания», рекламы и др.).
5) Дифференциальные уравнения в частных производных (процессы механических колебаний, теплопроводности, диффузии и др.).
6) Теория вероятностей, математическая статистика и теория случайных процессов (прогнозирование событий, статистическая обработка результатов измерений, марковские процессы, моделирование случайных процессов методом Монте-Карло и др.).
Инновационные содержательно-методические линии
Содержательно-методическую линию данной предметной области будем называть инновационной [17], если соответствующее содержание
– является востребованным на ступенях как общего (школьного), так и профессионального образования;
– определенной новизной, интегрирует формально-знаниевый и личностно-деятельностный подходы;
– является практически реализуемым и способным повышать эффективность деятельности субъектов образования;
– апробировано и по результатам апробации может быть внедрено и распространено (диффундировано).
Идея наполнения школьного курса задачами «реальной математики» не является новой, однако проблема выстраивания «сквозной» линии математических моделей, формирования соответствующего содержания и технологий нуждается в дальнейшей разработке. Содержательно-методическая линия математических моделей в школьном курсе приобретает особую актуальность в связи с утверждением в математическом образовании компетентностного подхода, и в частности, в связи с включением в контрольно-измерительные материалы ГИА за курсы основной и старшей школ задач компетентностно – ориентированного характера. Востребованность данной линии возрастает при переходе к профессиональному образованию. Так, во ФГОСах высшего образования, и в частности, актуализированных стандартах (например, ФГОС 3+ по направлению подготовки 08.03.01 «Строительство») среди требований к результатам освоения программы бакалавриата, указывается, что «…выпускник, освоивший программу бакалавриата, должен обладать следующими общепрофессиональными компетенциями:
– способностью использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и математического (компьютерного) моделирования, теоретического и экспериментального исследования (ОПК-1);
– способностью выявить естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности, привлечь их для решения соответствующий физико-математический аппарат (ОПК-2)».
В настоящее в образовательных организациях создаются инновационные площадки по апробации линии математических моделей. В частности, автором осуществляется научно-методическое сопровождение деятельности стажировочной площадки по мероприятию 2.4 «Модернизация технологий и содержания обучения в соответствии с новым федеральным государственным образовательным стандартом посредством разработки концепций модернизации конкретных областей, поддержки региональных программ развития образования и поддержки сетевых методических объединений» Федеральной целевой программы развития образования на 2016 год.
Таким образом, можно говорить о процессе обобщения и диссеминации эффективных моделей и технологий реализации Концепции развития математического образования в части линии математических моделей.
Выводы
В условиях перехода на новые федеральные образовательные стандарты общего (ФГОС) и высшего профессионального образования (ФГОС 3+) и реализации Концепции развития российского математического образования актуализируется проблема формирования практико – и профессионально-ориентированных умений средствами общеобразовательных предметных областей. Особую актуальность приобретает проблема сближения в учебном процессе «теоретической» и «реальной» математики, решаемая средствами эффективного использования идей и методов математического моделирования.
В этой связи мы предлагаем выделить в курсе математики «сквозную» содержательно-методическую линию математических моделей, в реализации которой заложен наибольший потенциал для роста мотивации учащихся к математической деятельности. Данная линия обладает признаками инновационности (востребованность, определенная степень новизны в содержании курса и методике его преподавания, практико-ориентированная направленность и др.). Реализация линии моделей направлена на формирование у учащихся компетенции математического моделирования, которую мы определяем как способность актуализировать и применять математические знания и умения при построении, анализе и интерпретации математических моделей в процессе решения учебных и практических задач.
Мы анализируем имеющиеся подходы к понятию математической модели, адаптируем соответствующий понятийно-категорийный аппарат к процессу решения учебных задач и демонстрируем на примерах процесс построения, анализа и интерпретации моделей.
Библиографическая ссылка
Нахман А.Д. ОСНОВНЫЕ АСПЕКТЫ ОБУЧЕНИЯ МАТЕМАТИЧЕСКОМУ МОДЕЛИРОВАНИЮ В СИСТЕМЕ «ШКОЛА-ВУЗ» // Научное обозрение. Педагогические науки. – 2016. – № 5. – С. 41-56;URL: https://science-pedagogy.ru/ru/article/view?id=1533 (дата обращения: 21.11.2024).