Теория вероятностей – это математическая наука, которая изучает законы существующей реальности, на которую влияют бесчисленные взаимосвязанные факторы, которые не поддаются какому-либо учету.
Как правило, методы анализа вероятностей в электроэнергетике делятся на два класса: аналитический и статический метод. Аналитические методы способны дать более широкое представление зависимости характеристики вероятности условий, но применение этих методов тесно связано с определенными математическими трудностями получения зависимостей. При использовании статических методов нам необходимо задействовать большой объем вычислений, а также немалое количества времени чтобы получить точные решения данной системы [1, 2].
На сегодняшний день крупнейшие электроэнергетические системы являются кибернетически сложными технические системы. Их аналитическое описание не представляется возможным [3]. В целях развития аналитические методов исследования этих система вводятся определённые допущения, к ним мы может отнести:
1. Упрощение структурных и математических моделей устройств и элементов
2. Функциональные преобразования законов распределения случайной величины;
3. Преобразование числовых характеристик;
4. Регрессионный анализ;
5. Факторный анализ;
6. Адекватный выбор закона распределения случайной величины.
Случайные явлениями называются такие явления, которые при повторном описании того же самого опыта происходят каждый раз по-разному. В системах электроснабжения случайными событиями, как правило, являются процессы изменения значений, характеризующих параметры режима: ток I (t), напряжение U (t), активная мощность P (t), реактивная мощность Q (t), происходящих во времени. Любая реализация определенных условий и действий, при которых наблюдается наблюдаемое случайное явление, называется опытом [4]. Примером может служить фиксирование активной энергии счетчиками через равные промежутки времени t дискретных значений мощности P в течение зимнего (летнего) рабочего дня. Результатами экспериментов являются фиксированные последовательности дискретных значений мощности (P) группы потребителей рабочей мощности. Событие, которое происходит в нас окружающем мире, является результатом воздействия большого количества других событий [5, 6].
Рис. 1. Последовательность дискретных значений
Для того чтобы понять, как элементы теории вероятностей и статистики используются на практике, решим несколько задач:
Задача 1: определить вероятность перерыва электроснабжения в схеме, если известны вероятности отказа элементов данной схемы:
qг = 4*10-3; qл = 4*10-3;
qT1 = 4*10-5; qT2 = 8*10-5.

Рис. 2. Схема передачи электричества
Решение: для начала нам необходимо определить вероятности безотказной работы данной системы. Она находится как противоположное событие:
pг = 1 – qг = 1 – 4*10-3 = 0,996
pT1 = 1 – qT1 = 1 – 4*10-5 = 0,99996
pл = 1 – qл = 1 – 4*10-3 = 0,996
pT2 = 1 – qT2 = 1 – 8*10-5 = 0,99992
Задачу можно решить двумя способами: согласно теореме сложения для совместных событий (метод 1) и через противоположные события (метод 2).
Метод 1:
Учитывая, что в системе могут выключиться сразу несколько элементов, то вероятность перерыва в цепи будет равна:
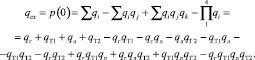
Подставляя значения, получим:
qcx ≈ 8,08546*10-3.
Также можно записать, что
qcx = qг + qТ1 + qл + qТ2 = 4*10-3 + + 4*10-5 + 4*10-3 + 8*10-5 = 8,1*10-3.
Если сравнить два полученных результата, то их погрешность будет равна 0,9 %. Из этого мы можем сделать вывод, что при соединении небольшого числа элементов в цепи, вероятность перерыва электричества будет равна сумме вероятностей отказал элементов, входящих в схему [7].
Метод 2:
В предыдущем методе решения вычисления были достаточно велики, а при увеличении числа элементов в цепи, будет увеличиваться и погрешность в расчётах. Но существует также и другой, более точный способ решения. Чтобы для потребителя дошла энергия, необходимо, чтобы все элементы цепи работали, а значит, используя теорему для умножения совместных событий, получим:
qcx = pгpТ1pT2pл.
Вероятность отказа системы найдем как противоположное событие:
qcx = 1 – qcx = 1 – pгpТ1pT2pл = 8,08546*10-3.
Ответ: qcx = 8,08546*10-3.
Задача 2: вероятность замыкания одной фазы линии электропередач P(A) = 0,02. Вероятность короткого замыкания третьей фазы, учитывая, что одна из трех фаз выведенных из строя P(B|A) = 0,3; вероятность короткого замыкания третьей фазы при условии, что две другие фазы сломаны P(C|AB) = 0,4. Необходимо найти вероятность поломки всей линии электропередач.
Полным выходом из строя ЛЭП называется поломка всех ее фаз, значит, вероятность этого события равна:
Решение:
P(ABC) = P(A)P(B?A)P(C?AB) =
= 0,02?0.3?0,4 = 0,0024.
Ответ: P(ABC) = 0,0024.
Задача 3: Дом обеспечивается электричеством от генератора или через трансформатор. Завтра, с 12.00 до 12.30, планируется остановка генератора на 20 минут, а также отклонение трансформатора на 15 минут. Необходимо найти вероятность того, что произойдет поломка блока питания в доме.
Решение: для начала нам необходимо обозначить прерывание электричества дома буквой А, произойдет оно или нет, будет зависеть от двух параметров: x – момента остановки генератора, а также y-момента отключения трансформатора. Значит, результат, который может связан с событием A, может быть представлен точкой E с координатами (x; y) на плоскости x-y, а за начало отсчета возьмем момент времени 12:00, за единицу измерения минуту. Пространство Ω всевозможных исходов Е, которые связаны с отключением генератора и трансформатора, будет представлять собой квадрат со сторонами по 30 минут каждая. Событие А произойдет только тогда, когда генератор и трансформатор будут выключены одновременно. Это условие может быть записано в виде системы неравенств:
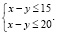
Первое неравенство соответствует случаю, когда трансформатор впервые выведен из эксплуатации, а второе-когда генератор впервые остановлен. Эта система на рисунке соответствует площади между соответствующими прямыми линиями. Событию соответствует точка пересечения этой области с помощью площади Ω [8].
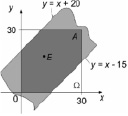
Рис. 3. Пространство всевозможных исходов
Площади областей Ω и S будут равны:
SΩ = 30*30 = 900
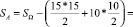
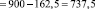 .
.
Тогда вероятность будет равна:
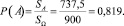
Ответ: P(A) = 0,819.
Задача 4: найти вероятность повреждения блока, который состоит из последовательно соединенных котла, турбины, и генератора, если вероятности повреждения отдельных блоков равны: qк = 0,03, qт = 0,02, qг = 0,01.
Вероятности целостности отдельных элементов:
pк = 1 – 0,03 = 0,97,
pт = 1 – 0,02 = 0,98,
pг = 1 – 0,01 = 0,99.
Найдем вероятность, что все элементы не повреждены:
pбл = pкpтpг ,
pбл = 0,97*0,98*0,99 = 0,941.
Далее найдем вероятность повреждение блока, как вероятность противоположную вероятности неповрежденного блока:
qбл = 1 – pбл ,
qбл = 1 – 0,941 = 0,059,
Ответ: qбл = 0,059.


 science-review.ru
science-review.ru