Scientific journal

Научное обозрение. Педагогические науки

ISSN 2500-3402

ПИ №ФС77-57475

Матрица – это прямоугольная таблица, которая представляет собой комплекс множества строк и столбцов, в ячейках могут находиться фрагменты заранее избранного множества – это те самые различные элементы или числа (комплексные, целые или векторы, которые зависит от самой задачи). Матрицы обозначаются прописными латинскими буквами. Дискретностью матрицы является совокупность m×n, где m-число строк, n-число столбцов. Также синонимом матрицы служит вектор [1].

Матричная алгебра является неотъемлемой часть в изучении экономики и дальнейшей её работе. Поясняется и трактуется это тем, что матричный вектор позволяет в доступной форме изложить экономическую ситуацию, также использование матрицы позволяет персоналу в различных сферах деятельности видеть результативность своей работы в целом. И также обратить минусы в неэффективности своей работы и сделать дальнейшие корректировки. С помощью вектора очень удобно записывать разные экономические закономерности и зависимости, ведь это очень компактно и удобно [2]. На практике матрицы могут быть представлены в совершенно различных формах и иметь самое различное содержание. Доказательством вышесказанных слов приведем табл. 1, в которой представлена статистика использования ресурсов.

Таблица 1

Использование ресурсов в различных сферах экономики

Эту таблицу можно записать и охарактеризовать в виде матрицы:

А =

Так, наглядно видно в таблице что, элемент матрицы а22 = 2,1 показывает, сколько водных ресурсов потребляет аграрная промышленность во всех сферах экономики, а следующий элемент матрицы а13 = 6,7 демонстрирует, сколько трудовых ресурсов потребляет рынок в целом.

Наглядным примером также может нам послужить следующая задача:

Некая фирма производит различную продукцию С1, С2, С3 и на изготовку этого продукта используется материал К1, К2:

А =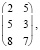

где элемент аij показывает сколько сырья j-того типа может быть потрачено внутри организации на производство продукции i-того типа. Цена каждого вид сырья равна:

C =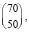

а планирование выпуска продукции равно В = (110 150 70).

Из этого следует как, мы получим: расходы на материал

К1 = 2×110 + 5×150 + 8×70 = 1530,

а цена другого материала

К2 = 5×110 + 3×150 + 7×70 = 1490.

Таким образом, суммарная цена материала Р = 1530×70 + 1490×50 = 181600 может быть представлена в виде вектора:

Р = К×С = (ВА)С = 181600.

Заметим, что суммарную цену материала P можно вычислить и в совсем иной последовательности: изначально, вычислим вектор Z стоимость всех затрат материалов:

Z = A*C =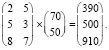

Суммарная цена материала равна:

P = B*Z = (110 150 70)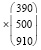 = 181600.

Идентичность всех выше перечисленных результатов (181600) была получена благодаря правильному выполнению семантического закона умножения векторов: (ВА)С = В(АС).Этот закон ярко иллюстрирует пример такого, что решая через любой вид решения матриц можно добиться одинаковости всех результатов [3].

В табл. 2 проиллюстрированы сведения о работе 5 различных фирм, которые выпускают 4 вида товара с потреблением 3-х видов сырья, так же количество времени работы абсолютно каждой фирмы в году и стоимости всех видов материала.

Следовательно, должны понять:

1) Эффективность и плодотворность всех фирм по каждому виду продукции.

2) Нужда всех фирм по каждому виду материала.

3) Совокупность кредитования фирм для закупки и переработки материалов, которые необходимо для выпуска продукции указанных видов и количеств фирм.

Выстроим матрицу производства фирм по всем типам продукции:

C =

Столбец вектора полностью соответствует производству по каждому типу изделия. Так годовое производство i-ой фирмы по каждому виду продукции можно произвести за счет произведения i-го столбца вектора C на количество рабочих дней в году именно для фирмы (i = 1, 2 ,3). Поэтому, годовое производство каждой фирмы по каждой продукции можно выразить с помощью вектора:

С1 =

Матрица затрат материалов на единицу продукции представлена как:

D =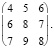

Все издержки по видам материала на фирмах можно полностью расписать как D*C:

DC =

где j-я строка соответствует номеру типа материала, а i-й столбец – номеру фирмы согласно таблице (j = 1, 2, 3; i = 1, 2, 3).

Ответ на второй вопрос, который был поставлен в задаче, можно получить таким же образом, что в первом, аналогично произвести произведение столбцов вектора DС нужда фирмы во всех типах материала:

DC1 =

Введем вектор цены материала: Q= (70, 80, 90)

Тогда цену годового запаса материала для каждой фирмы можно получить произведя операцию над матрицами, а точнее умножением матриц, следовательно ,вектора Q на матрицу DC1:

P = QDC1 = (8238300 8979200 4937400).

Хочется сказать о том, что, суммы кредитования фирм для закупки материала определяются путем аналогии всех компонентов вектора P.

Подводя итоги вышесказанному можно сказать о том, что в современной математике и экономике векторы играют важную роль и являются неотъемлемой часть ее. Активно могут быть использованы в различных теориях, в экономике, менеджменте и многих других разделах естествознания и наукознания, не говоря уже о применении матриц в разных направлениях учебной деятельности [4].

Мы смогли выявить лишь один недостаток, Он заключается в том ,что по матрицам крайне сложно, даже практически невозможно определить победителя в каких-то сферах деятельности.

Также хочется отметить ряд огромных плюсов и достоинств матриц : Во-первых, они позволяют форме записывать на простом и доступным языком различные экономические процессы и закономерности в различных организациях и не только ,во-вторых, благодаря им решаются самые сложные задачи, которые могут показаться почти невыполнимыми, что является наиболее значимым для экономистов [5]. В-третьих, с помощью матриц можно за короткий промежуток времени, сил и труда полностью проанализировать и решить множество задач. И можно сказать о том, что при присутствии каких-либо отрицательных факторов применения матричной алгебры положительные моменты превосходят в несколько раз.