science-review.ru
Игра – исторически обусловленный, естественный компонент культуры, отображающий собой вид произвольной деятельности индивида. В игре совершается повторение и взаимообогащение социального навыка предыдущих поколений, овладение нормами и правилами человеческой жизнедеятельности через добровольное принятие игровой роли, виртуальное представление игрового пространства, условий своего собственного бытия в мире. В таком случае имеется то, что игра считается одним из методов изучения человеком мира и взаимоотношений в нем, способом самоутверждения человека, заключающий в произвольном конструировании действительности в условном проекте. В качестве средства, метода и технологии преподавания различные игры обширно применяются в педагогическом процессе [1].
П.И. Пидкасистый и Ж.С. Хайдаров разделяют все детские игры на следующие виды:
1. Психологические и физические игры и тренинги:
– двигательные (спорт, мобильные, моторные);
– экстатические, экспромтные игры и развлечения;
– освобождающие игры и забавы – целебные игры (игротерапия).
2. Интеллектуально – творческие игры:
– предметные забавы
– сюжетно-умственные игры
– дидактические игры (учебно-предметные, обучающие, познавательные)
– строительные, трудовые, промышленные, конструкторские
– электронные, компьютерные игры
– игровые методы обучения
3. Социальные игры:
– творческие, сюжетно-ролевые (подражательные, режиссерские, игры – презентации)
– деловые игры (организационно-деятельностные, организационно-коммуникативные, организационно-мыслительные, ролевые, моделирующие)
4. Комплексные игры (коллективно-творческая досуговая деятельность) [2].
Важной проблемой преподавания математики является формирование мотивационной сферы обучения школьников. Для развития устойчивого познавательного интереса у обучающихся к математике используют разнообразные математические игры. Применяя на уроках актуальные технологии и методы обучения, помогающие активизировать мысли школьников, которые развивают в них любознательность и глубокий познавательный интерес, стимулируют учеников к самостоятельному приобретению знаний, учителя смогут решить эту проблему. Одной из таких технологий является игровая технология [1].
Игровая технология обучения – это такая организация учебного процесса, при котором обучение осуществляется путем вовлечения учащихся в учебную игру.
Дидактическая игра как форма работы занимает важное место в развитии познавательного интереса у обучащихся и оказывает особое влияние на их деятельность.
Проведение урока в игровой форме помогает активизации мыслительной деятельности школьников, увеличивает концентрацию внимания, настойчивость, работоспособность, интерес, создает условия для появления радости успеха, удовлетворенности, чувства коллективизма. Введение в урок элементов игры разрушает интеллектуальную пассивность обучащихся, возникающая после длительного умственного труда на уроках. Учебная игра формирует способность принимать самостоятельные решения, проводить самооценку и оценивать работу своих товарищей, а также вырабатывает целеустремленность.
Различают следующие виды дидактических игр:
– игры-упражнения,
– игры-путешествия,
– деловая игра,
– сюжетная (ролевая) игра,
– игра-соревнование.
Чтобы обеспечить выполнение дидактических игр на уроках математики, желательно: определить цель, выявить, какие умения и навыки учащиеся могут освоить во время игры; определить место игры в учебном процессе на уроке, ее продолжительность; разработать правила игры, продумать время ознакомления с этими правилами (до игры, на самом уроке или за несколько уроков, вывесив правила игры на стенде и в классной комнате); предусмотреть занятость учащихся, которые будут необходимы в ходе игры; продумать механизм оценки качества результатов деятельности каждого участника игры и группы (команды) в целом при подведении итогов игры по активности; определить форму подведения итога игры по содержанию (вывод, формулирование основного теоретического положения, обобщение).
Использование дидактической игры на уроке обеспечивает не только индивидуальную, но и парную, групповую и коллективную форму работы школьников [3].
Игровые технологии на уроках математики используются на разных ступенях обучения.
В начальной школе дидактическая игра способствует снять чувство усталости, выявляет способности детей, их индивидуальность, усиливает непроизвольное запоминание.
Данная ступень обучения содействует формированию универсальных учебных действий, т.к. именно в этот период у детей происходит плавный переход от игровой деятельности к учебной. Для учеников начальной школы часто используют такие игры как: ролевые игры на уроке (инсценировки), урок-соревнование, урок-конкурс, урок-путешествие, урок – КВН.
Несмотря на простоту технологии, дидактические игры используют и в старших классах. Многие условия игр моделируют реальные ситуации, в которые погружаются обучающиеся и могут применить на себя разные роли, что не только способствует познавательной активности, но и выбору будущей профессии. Получаем «взрослые» игры. Финансовые задачи, повышение экономической грамотности, создание и проведение брейн-рингов.
Подбирая задачи для игр лучше иметь ввиду то, что ученикам не интересно решать то, что им не пригодится в жизни. Поэтому, на мой взгляд, лучше всего подойдут задачи с «реальными» условиями. Например, можно использовать задачи на проценты, банковские кредиты. Тем более часто такие задачи встречаются в ЕГЭ. Рассмотрим примеры задач с решениями, которые можно включить в игру «Брейн-ринг».
Задача 1. Инженер-конструктор разработал схему вантового моста. Вертикальные пилоны соединены провисающей цепью. Тросы, свисающие с цепи и поддерживающие полотно моста-вантами.
Введём систему координат: ось Oy направим вертикально вдоль одного из пилонов, а ось Ox направим вдоль полотна моста, как показано на рисунке.
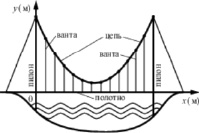
В этой системе координат линия, по которой провисает цепь моста, имеет уравнение y = 0,015x2 – 0,86x + 20, где x и y измеряются в метрах. Найдите длину ванты, расположенной в 35 метрах от пилона [4].
Решение. Задача сводится к вычислению значения y(35) найдём его:
y = 0,015?352 – 0,86?35 + 20 = = 18,375 – 30,1 + 20 = 8,275.
Задача. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5 %, затем 12 %, потом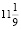 
% и, наконец, 12,5 % в месяц. известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на 
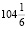% Определите срок хранения вклада [5].
Решение: Нам известно, что проценты на вклад начислялись ежемесячно. Также каждая последующая процентная надбавка по истечении календарного месяца начислялась с учетом вновь образованной суммы вклада и с учетом предыдущих надбавок.
Если первоначальная сумма вклада при ежемесячной 5 %-ной ставке начисления процентов продержалась месяцев, то вклад ежемесячно увеличивался в 1 + 5?0,01 раз, и этот коэффициент будет сохранен до тех пор, пока ставка не изменится.
При изменении процентной надбавки с 5 % на 12 % (ставка 12 % продержалась m месяцев) первоначальная сумма вклада за (k + m) месяцев увеличится в (1 + 0,05)k× ×(1 + 0,12)m =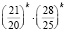 
раз.
Предположим, что процентная ставка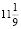 
продержалась n месяцев, а процентная ставка 12,5 продержалась t месяцев. Тогда соответствующие коэффициенты повышения составят
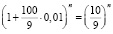и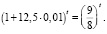 
Таким образом, коэффициент повышения суммы вклада в целом за весь период хранения вклада в банке составит:
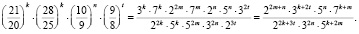
Это – с одной стороны. Но с другой стороны, согласно условию задачи первоначальная сумма вклада за это же время увеличилась на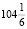 
то есть в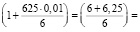 
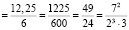(раз).
Значит,
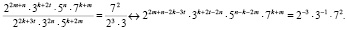
Согласно основной теореме арифметики каждое натуральное число, большее 1, можно представить в виде произведения простых множителей, и это представление единственное с точностью до порядка их следования. В таком случае: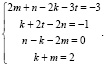 
Решим эту систему относительно натуральных k, m, n и t.
Из последнего уравнения системы имеем: k = m = 1 При этих значениях k и m система примет вид:
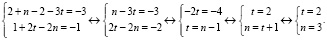
Итак, k + m + n + t = 1 + 1 + 3 + 2 = 7 вклад в банке на хранении был 7 месяцев. При найденных значениях k, m, n и t n – k – 2m действительно равно нулю.