В условиях современного промышленного производства все чаще применяются методы математического моделирования технологических процессов, позволяющие решать задачи прогнозирования и оптимизации производства [1]. В настоящее время одной из наиболее актуальных проблем при проведении экспериментальных исследований является проблема извлечения максимального количества полезной информации об исследуемом процессе при минимальных затратах. При решении производственных задач и недостаточном знании механизмов протекания процессов не всегда существует возможность выполнять достаточное количество требуемых экспериментов. Поэтому становится целесообразным построение математических моделей с использованием методов планирования эксперимента [2]. В связи с этим разработка математической модели является актуальной работой.
В данном исследовании предложена математическая модель процесса получения полимеров стирола.
Из полистирола производят большое количество пластиков. Распространение он получил благодаря своей простоте, невысокой цене и широкому ассортименту марок. Из вещества получают массу предметов, которые стали неотъемлемой частью нашей повседневной жизни (детские игрушки, упаковка, одноразовая посуда и так далее).
Механизм реакции получения полистирола можно представить в следующем виде:
1) Распад инициатора (образование радикалов, инициирующих полимеризацию)
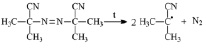
2) Рост цепи
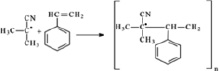
3) Обрыв цепи
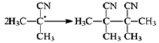
– обрыв цепи в результате взаимодействия с радикалом
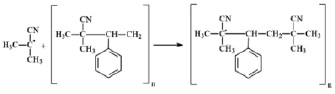
Кинетический метод моделирования полимеризационных процессов заключается в составлении и численном решении кинетических уравнений для концентрации частиц, участвующих в процессе [3].
Кинетическая схема полимеризации стирола включает следующие элементарные стадии:
1. Инициирование свободных радикалов
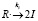
2. Рост цепи
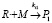
3. Продолжение цепи
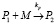
…
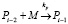
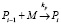
4. Рассмотрим один из вариантов обрыва цепи
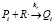
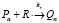
где M – мономер, R – свободный радикал, I – инициатор, Pn, Qn – активные («растущие») и неактивные («мертвые») цепи сополимера длиной n, соответственно, содержащие n звеньев M.
Получим систему обыкновенных нелинейных дифференциальных уравнений, описывающую процесс полимеризации стирола. Составим кинетические уравнения по продуктам полимеризации: активным цепям полимера Pi и неактивным цепям полимера Qi. Кинетические уравнения составляются на основании закона действующих масс, согласно которому скорость реакции равна произведению константы скорости и концентраций реагентов [4]. Математическая модель примет вид:
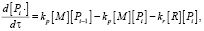
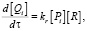 (1)
(1)
где […] – концентрации соответствующих веществ ([M] – мономера, [R] – свободного радикала, [I] – инициатора, [Pn], [Qn] – активных («растущих») и неактивных («мертвых») цепей сополимера длиной n, соответственно, содержащие n звеньев M мономера).
Статистическая теория полимеризации исходит из предположения о возможности анализа молекулярно-массовых распределений (ММР) по средним молекулярным массам Mn, Mω (низкомолекулярной и среднемолекулярной частей соответственно). Для их анализа используются понятия моментов, обычно применяемые в статистике и теории вероятностей для оценки распределения случайных величин [5].
Для моментов любого порядка по определению имеем:
mj = μj + ηj, (2)
ηj, μj – моменты j – порядка активных и неактивных цепей полимера, рассчитываемые по формулам:
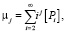 (3)
(3)
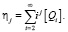 (4)
(4)
Для подстановки моментов в систему (1) помимо самих выражений (3)-(4), необходимо определение производных μj и ηj по времени, которые можно найти по следующему правилу:
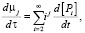 (5)
(5)
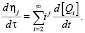 (6)
(6)
Перепишем ранее полученную систему (1) в систему дифференциальных уравнений относительно моментов распределения μj и ηj. Для этого требуется найти значения μ0(t), μ1(t). Из формулы (5) получим выражения для моментов в виде:
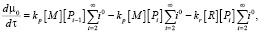 (7)
(7)
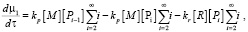 (8)
(8)
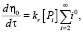 (9)
(9)
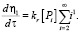 (10)
(10)
Произведение 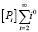 представляет собой μ0, поэтому уравнение 7 можно переписать
представляет собой μ0, поэтому уравнение 7 можно переписать
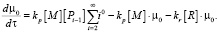 (11)
(11)
Аналогично 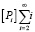 представляет собой μ1, поэтому уравнение 8 можно переписать
представляет собой μ1, поэтому уравнение 8 можно переписать
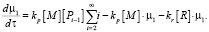 (12)
(12)
В соответствии с принципом стационарных концентраций – время существования активных частиц (радикалов) бесконечно мало, поэтому изменение их концентраций принимают равным нулю. Если приравнять уравнения 10-11 к нулю, то можно выразить μ0, μ1, и далее использовать для расчета среднечисленной молекулярной массы Mn(t) [6].
Величина Mn определяет среднюю длину макромолекул полимера и называется среднечисленной молекулярной массой. Она рассчитывается по следующей формуле:
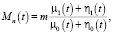 (13)
(13)
где m – молекулярная масса мономера.
Таким образом, для процесса полимеризации построена математическая модель, представленная в виде системы обыкновенных дифференциальных уравнений.
С помощью данной модели получено выражение для среднечисленной молекулярной массы.


 science-review.ru
science-review.ru