Научный журнал

Научное обозрение. Педагогические науки

ISSN 2500-3402

ПИ №ФС77-57475

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Елизаров А.В. 1 Покровский В.Г. 1

---

1 Пензенский государственный технологический университет

Повышение качества и сокращение сроков проектирования изделий приборостроения в современных условиях невозможно без привлечения средств автоматизации проектных и конструкторских работ. До недавнего времени автоматизация проектных работ сводилась к производству графической проектной документации. Теперь от системы автоматизированного проектирования требуется выполнять весь комплекс расчётов на механические воздействия, расчёт температурных режимов объекта проектирования, расчёт помехозащищённости и электромагнитной обстановки и т.д. Целью исследования является разработка способа построения систем уравнений для определения составляющих обобщённых сил по направлениям координатных осей для решения задач оптимизации структуры проектируемых конструкций электронной аппаратуры и приборов. В процессе выполнения исследования использовались: метод конечных элементов; положения линейной теории упругости; математический аппарат импликативной алгебры выбора. Описан способ построения систем алгебраических уравнений и определения составляющих обобщённых сил по направлениям координатных осей. Способ может быть применён для решения задач моделирования и структурной оптимизации конструкций электронной аппаратуры. Использование математических моделей конструкций с нефиксированным количеством переменных проектирования позволяет в процессе решения задачи моделирования выполнять преобразования моделей конструкций. Таким образом, становится возможным решать задачи оптимизации структуры проектируемой конструкции. Использование математических моделей конструкций с нефиксированным количеством переменных проектирования позволяет в процессе решения задачи моделирования выполнять преобразования моделей конструкций. Таким образом, становится возможным решать задачи оптимизации структуры проектируемой конструкции.

Статья в формате PDF

838 KB

напряжённо-деформированное состояние

конструкции электронной аппаратуры

автоматизация проектирования

инженерный анализ конструкций

оптимизация конструкций.

1. Курносов В.Е., Покровский В.Г. Предикатная алгебра выбора в задачах проектирования нагруженных конструкций радиоаппаратуры и приборов // Проблемы исследования и проектирования машин: сборник статей Международной научно-технической конференции. – Пенза: ПДЗ, 2005. – С. 23–28.

2. Покровский В.Г. Программный комплекс синтеза конструкций на основе эволюционных дискретных моделей // Современные технологии в машиностроении: сборник статей XII Международной научно-практической конференции. – Пенза: Приволжский дом знаний, 2008. – С. 147–151.

3. Покровский В.Г. Информационные технологии в проектировании несущих конструкций электронной аппаратуры на основе эволюционных дискретных моделей // XXI век: итоги прошлого и проблемы настоящего плюс: Научное периодическое издание. – Пенза: Изд-во Пенз. гос. технол. акад., 2012. – № 05(09). – Пенза, 2012. – С. 198–204.

4. Покровский В.Г. Программный комплекс структурной оптимизации стержневых несущих конструкций на основе импликативной алгебры выбора // Информационные системы и технологии: Научно-технический журнал. – Орёл: ФГБОУ ВПО «Государственный университет – учебно-научно-производственный комплекс» (Госуниверситет – УНПК), 2013. – № 2(76). – С. 251–260.

5. Покровский В.Г. Структурная оптимизация и декомпозиция конструкций электронной аппаратуры на основе эволюционных дискретных моделей // Вестник Томского государственного университета. Математика и механика: Научный журнал. – Томск: Национальный исследовательский Томский государственный университет, 2016. – № 05(43). – С. 73–82.

Повышение качества выпускаемой продукции, а также сокращение сроков освоения и внедрения новой техники, возможно при условии применения средств автоматизации проектно-конструкторских работ. Неотъемлемой частью процесса автоматизированного проектирования новых изделий является решение задач моделирования этих изделий при заданных эксплуатационных воздействиях. Это возможно реализовать с помощью программно-технических комплексов, реализующих технологии автоматизированного проектирования и моделирования. Такие комплексы могут быть построены на основе использования численных методов анализа физических процессов в проектируемых конструкциях.

При решении задач оптимизации и изменении структуры модели проектируемой конструкции возникает необходимость в модификации математической модели проектируемой конструкции. Как следствие, изменяется количество переменных проектирования. Для осуществления модификации математической модели объекта проектирования требуется использовать соответствующий математический аппарат предметно-ориентированной логики. На основе такого математического аппарата можно строить логико-алгебраические выражения, используя которые можно вводить и исключать переменные и функции. Это даёт возможность создавать математические модели проектируемых изделий с нефиксированным количеством переменных проектирования.

Разработка программно-технических комплексов автоматизированного проектирования и имитационного моделирования, позволяющих решать задачи структурной оптимизации проектируемых конструкций, является актуальной. Решение задач оптимизации объектов проектирования, которые обладают дискретной структурой, возможно при условии применения математических моделей с нефиксированным количеством переменных проектирования.

Для того, чтобы задать проект стержневой системы, назначаются переменные проектирования. В качестве переменных проектирования элементов стержневой системы можно рассматривать: геометрические параметры поперечных сечений стержневых элементов, координаты их торцевых граней, физико-механические характеристики материала конструкции [1].

Для создания формализованного описания процедуры удаления дискретного элемента модели конструкции используется операция предикатной дизъюнкции аппарата импликативной алгебры выбора. Матрица-вектор переменных проектирования дискретного элемента стержневой системы 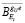является аналогом предметной переменной yi. Выбор или исключение дискретного элемента стержневой системы определяется как выбор или исключение матрицы-вектора переменных проектирования дискретного элемента 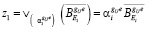[1]:

. (1)

Из уравнений, описывающих поведение стержневой системы, определяются переменные состояния. В качестве переменных состояния можно рассматривать составляющие смещений торцевых граней стержня [2]:

. (2)

Сумма узловых реакций определяется как скалярное произведение матрицы-вектора составляющих узловых смещений и матрицы-вектора узловых составляющих жёсткостей 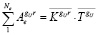[3]:

. (3)

Из матриц жесткостей стержней выделяются вектор-строки, соответствующие силовым составляющим

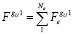
по направлению координаты Х. Составляющая 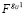определена как проекция обобщенной узловой силы на координатную ось X. Вектор-строки соответствуют матрицам-векторам составляющих жесткостей стержневых элементов [4].

Сумма составляющих узловых сил (проекций на ось X), соответствующих узлу сетки с координатами i, j, k определяется как скалярное произведение матрицы-вектора составляющих смещений 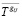и матрицы-вектора узловых составляющих жесткостей :

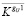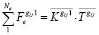. (4)

Из выражения (3) формируется уравнение для вычисления узлового смещения, относящегося к узлу с координатами i, j, k. [2]:

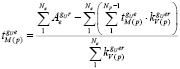. (5)

Составляющая обобщённой силы, соответствующая смещению V по направлению координаты Y:

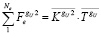. (6)

Составляющая обобщённой силы, соответствующая смещению W по направлению координаты Z:

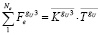, (7)

Составляющая обобщённого момента, соответствующая углу поворота ΘX:

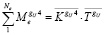. (8)

Составляющая обобщённого момента, соответствующая углу поворота ΘY:

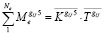. (9)

Составляющая обобщённого момента, соответствующая углу поворота ΘZ:

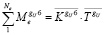. (10)

Из соотношений (4), (6) – (10) определяются смещения и углы поворотов торцевых граней стержневых элементов (5). По найденным линейным и угловым смещениям, вычисляются механические напряжения в элементах конструкции [5].

Ниже приведено решение задачи структурной оптимизации стержневой конструкции при одновариантном механическом нагружении. Начальная структура представлена объёмной конструкцией, выполненной из элементов в виде труб из стали квадратного сечения со стороной 40 мм, количество стержневых элементов – 600 шт.; масса конструкции —1763,448 кг; силовые воздействия по направлению оси Y – 7000 Н; длина заготовки по оси Х – 10 м; высота по оси Y – 2 м; глубина по оси Z – 1 м. Сеточная модель исходной конструкции изображена на рисунке 1. На этом же рисунке условно изображены силовые воздействия, которые локализованы в узлах нижнего пояса сеточной модели конструкции. Также, в нижнем поясе сеточной модели условно изображены опоры, которые моделируют жёсткое закрепление конструкции для предотвращения вертикальных смещений конструкции.

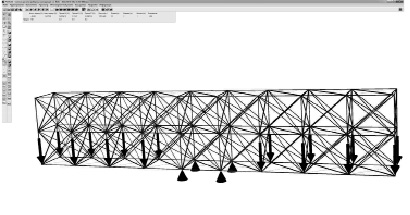
Рис. 1. Сеточная модель конструкции в главном окне программного комплекса

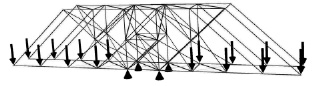
Рис. 2. Тринадцатый шаг структурной оптимизации. Конечная структура

Результаты решения задачи оптимизации структуры конструкции: время решения – 36 с.; количество стержневых элементов – 226 шт.; масса конструкции – 674,234 кг; максимальная перегрузка – 48,66 %; максимальный прогиб – 0,1 % при норме 0,1 %.

Задача оптимизации структуры конструкции была решена в автоматическом режиме. На рис. 2 представлен результат решения задачи оптимизации. Последующее удаление стержневых элементов из конструкции приводит к ухудшению её прочностных свойств, поэтому структура, изображённая на рис. 2, является конечной.

Подобные конструкции могут использоваться в качестве опорных элементов для размещения радиоэлектронных устройств. Масса устройств в данном случае моделируется силовыми воздействиями по направлению вертикальной координатной оси.

Разработанная методика формальной оптимизации конструкций позволяет модифицировать исходную конструкцию, обладающую избыточной массой и структурным составом в более совершенную конечную конструкцию, которая является оптимальной с точки зрения эксплуатационных воздействий и конструкторско-технологических ограничений. Применяемые модель пространственной стержневой системы и программный комплекс позволяют выполнять структурную оптимизацию конструкций в автоматическом режиме. Это даёт возможность сократить сроки и стоимость проектных работ и программу испытаний проектируемых изделий.

Библиографическая ссылка