science-review.ru
Введение
Для большинства задач в курсах высшей математики современные технологии позволяют обеспечить автоматическую генерацию и проверку заданий [1, 2]. При таком подходе к формированию контрольно-измерительных материалов необходимо предусмотреть ряд факторов: неоднозначность проверяемого ответа, сложность арифметических вычислений при случайной генерации условий [3]. Алгоритмы автоматической проверки ответов также должны учитывать не только итоговый ответ, но и ход решения [4, 5], этого можно добиться, выделив контрольные точки при решении задачи [6, 7].
Для студентов инженерных специальностей, обучающихся в МГТУ имени Н.Э. Баумана, кафедра «Вычислительная математика и математическая физика» разработала электронные интерактивные курсы дисциплин математического цикла на базе информационной образовательной среды Nomotex, генерация заданий и проверка ответов осуществляется в автоматическом режиме [8, 9].
В рамках курса «Аналитическая геометрия» студенты изучают раздел «Системы линейных алгебраических уравнений» (далее СЛАУ), который является одним из основных и наиболее важных, так как подобные системы широко используются в задачах физики, химии, экономики и других науках [3]. Задача решения именно СЛАУ довольно редко представляет самостоятельный интерес для прикладных задач, но, например, большое количество численных методов решения нелинейных задач предусматривает решение СЛАУ в качестве элементарного шага алгоритма [7, 10].
Системы линейных уравнений не всегда имеют одно-единственное решение, в таких случаях форма ответа определяется неоднозначно. Для исключения неоднозначности следует в первую очередь использовать простую и понятную форму для ввода ответа, а также, в случае СЛАУ, реализовать возможность проверки ответа с точностью до константы. Платформа Nomotex предоставляет весь необходимый функционал для реализации таких алгоритмов [6, 7].
Решение СЛАУ предполагает несколько шагов, каждый из которых является отдельной математической компетенцией, которая должна оцениваться отдельно и составлять часть от общего балла за задачу [8]. К таким навыкам можно отнести: составление основной матрицы СЛАУ, приведение матрицы к ступенчатому виду, проверку совместности системы, нахождение всех решений СЛАУ, нахождение фундаментальной системы решений. Возможность проверки уровня владения каждым навыком можно реализовать с помощью формы ввода ответа, а также в алгоритмах автоматической проверки [3, 7]
Целью исследования является разработка и реализация алгоритмов автоматической генерации и проверки задач на решение систем линейных алгебраических уравнений, а также системы автоматического оценивания при проверке введенного решения.
Материалы и методы исследования
Все методы и алгоритмы, разработанные авторами, реализованы на базе информационно-образовательной среды Nomotex. Рассматривается система линейных алгебраических уравнений:
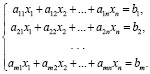(1)
Величины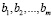 
называют свободными членами уравнений, 
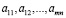– коэффициентами системы, которые предполагаются известными, а 
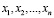– неизвестными, подлежащими определению. В случае, когда коэффициенты 
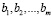одновременно равны нулю, системы уравнений называют однородной (ОСЛАУ), в противном случае неоднородной (НСЛАУ). В матричном виде систему уравнений (1) можно записать следующим образом:
(2)
где А – основная матрица СЛАУ, Х− столбец неизвестных, В – столбец свободных членов.
В рамках изучения курса «Аналитической геометрии» рассматриваются способы решения СЛАУ, но наиболее универсальным является метод Гаусса, который позволяет найти решения как определенных, так и неопределенных систем уравнений.
При нахождении всех решений СЛАУ можно выделить следующие основные шаги, которые могут проверяться и оцениваться в отдельности друг от друга, что позволяет при автоматической проверке исключить ситуацию с начислением баллов по правилу «всё или ничего».
1. Приведение расширенной матрицы системы уравнений к ступенчатому виду, пока одна из переменных не выразится явным образом, и проверка СЛАУ на совместность по теореме Кронекера – Капелли.
2. Определение количества свободных k (независимых) переменных, через которые выражаются остальные неизвестные. Они возникают в случае, если ранг матрицы меньше числа неизвестных и их количество можно определить как разность числа неизвестных и ранга матрицы: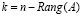 
3. Выбор базисных переменных и нахождение общего решения СЛАУ.
4. Запись общего решения системы.
Также для борьбы со списыванием с помощью увеличения числа вариантов авторами был разработан алгоритм генерации условий задач. Большое внимание при этом уделялось вычислительной сложности задачи, подбор коэффициентов СЛАУ осуществлялся таким образом, чтобы минимизировать вероятность арифметической ошибки. Поэтому уравнения составлялись таким образом, чтобы в процессе решения не появлялись дробные значения и большие числа, которые трудно вычислять в уме. Для достижения вышеуказанных целей авторами был реализован следующий алгоритм генерации условий:
1. Указывается, сколько уравнений будет в системе уравнений – k .
2. Сколько в системе будет неизвестных – r.
3. Сколько независимых решений будет в ответе – n.
Под третьим пунктом подразумевается, что система уравнений может быть линейно зависимой, и тогда число решений будет бесконечным, которое может быть выраженно в виде линейной комбинации независимых решений.
4. Далее формируем r – n уравнений следующим образом:
.
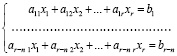5. Коэффициенты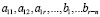 
– целые числа по модулю, не превосходящие 10, коэффициент a11 всегда равен ±1, что позволяет начать приведение матрицы к ступенчатому виду без первоначальных преобразований. Эти уравнения должны быть линейно независимы, поэтому проверяем, чтобы ранг матрицы составленной из коэффициентов сгенерированных уравнений был равен r – n
6. Остальные k – (r – n) получаем из линейной комбинации уравнений, сгенерированных на предыдущем шаге, коэффициенты линейной комбинации – это целые числа по модулю, не превосходящие 5.
Результаты исследования и их обсуждение
Используя описанные принципы и алгоритмы, авторы разработали на платформе ИОС Nomotex ряд типовых заданий.
Задача на нахождение решений ОСЛАУ. В данной задаче студенту на первом этапе необходимо определить, имеет ли система решение, отличное от нулевого, то есть нетривиальное, и далее указать ранг расширенной матрицы системы. На последнем этапе требуется ввести общее решение системы уравнений. На рис. 1 изображена форма для ввода ответа на задачу в ЦОС Nomotex.
Изначально студент выявляет наличие или отсутствие нетривиального решения и выбирает соответствующий ответ в поле ввода: «Да» или «Нет». Далее вводит ранг расширенной матрицы. Поле ввода общего решения ОСЛАУ появится только в том случае, если студент указал, что система имеет ненулевое решение. Количество столбцов при вводе общего решения ОСЛАУ можно изменять соответствующими кнопками «+» и «−».
Алгоритм проверки в данной задаче следующий:
1. Проверка поля ввода о наличии нетривиального решения и сравнение ранга расширенной матрицы со значением, прописанным в системе ЦОС Nomotex.
2. Сравнение числа линейно независимых решений для ОСЛАУ со значением, прописанным в системе ЦОС Nomotex.
3. Проверка на то, что введенные студентом ответы являются ненулевыми и линейно независимыми.
4. Подстановка решений в исходную систему.
Рис. 1. Форма ввода ответа для задачи на нахождение общего решения ОСЛАУ
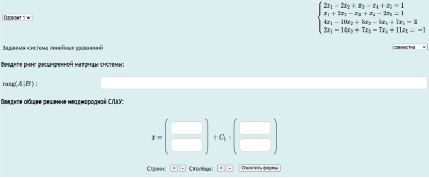
Рис. 2. Форма ввода ответа для задачи на нахождение общего решения НСЛАУ
Рис. 3. Форма ввода ответа для задачи на нахождение общего решения НСЛАУ при различных значениях параметра λ
Приведенный выше алгоритм автоматической проверки позволяет оценить по отдельности каждый этап решения задачи, баллы студенту начисляются следующим образом:
1. За верно найденный ранг расширенной матрицы студенту начисляется 0,3 от полного количества баллов за задачу.
2. Оставшиеся баллы за задачу студенту начисляются в случае верного нахождения общего решения ОСЛАУ.
Задача на нахождение решений НСЛАУ. Решение данной задачи требует от студента выполнения следующих шагов: составление расширенной матрицы системы, приведение ее к ступенчатому виду и определение ранга, проверка совместности СЛАУ и на последнем этапе нахождение общего решения. На рис. 2 изображена форма для ввода ответа на задачу в ЦОС Nomotex, предусматривающая проверку каждого этапа решения.
На первом этапе студенту необходимо определить, имеет ли система решение, ввести результат в соответствующее поле, после чего, если система совместна, появится возможность для ввода общего решения НСЛАУ. Так же как и в предыдущей задаче, найти ранг расширенной матрицы. Количество форм для ввода общего решения НСЛАУ регулируется соответствующими кнопками «+» и «−».
Алгоритм проверки данной задачи следующий:
1. Проверка поля ввода о совместности системы и сравнение ранга расширенной матрицы со значением, прописанным в системе ЦОС Nomotex.
2. Сравнение числа линейно независимых решений для ОСЛАУ со значением, прописанным в системе ЦОС Nomotex.
3. Проверка на то, что введенные студентом ответы являются ненулевыми и линейно независимыми для однородной системы.
4. Подстановка частного решения в исходную систему и подстановка линейно независимых решений в однородную систему.
Данный алгоритм позволяет оценивать каждый этап решения задачи в отдельности. Такой подход позволяет дать обратную связь и указать на ошибки, допущенные в ходе решения, что особенно важно при самостоятельной проработке заданий. При проверке заданий этого типа баллы начисляются по следующему принципу:
1. За верно найденный ранг расширенной матрицы студенту начисляется 0,3 от полного количества баллов за задачу.
2. Оставшиеся баллы за задачу студенту начисляются в случае верного нахождения общего решения НСЛАУ.
Задача на нахождение решений НСЛАУ, зависящей от параметра. В данной задаче студенту нужно исследовать и найти решение, если оно существует, системы линейных алгебраических уравнений при различных значениях параметра λ. На рис. 3 изображена форма для ввода ответа на задачу в ЦОС Nomotex.
Сначала студенту требуется определить, при каких значениях параметра λ НСЛАУ будет являться совместной. После чего определить количество линейно независимых решений для ОСЛАУ и далее записать общее решение НСЛАУ при соответствующем параметре λ. Количество форм для ввода общего решения НСЛАУ регулируется кнопками «+» и «−».
Алгоритм проверки данной задачи следующий:
1. Сравнение значения параметра λ и числа линейно независимых решений для ОСЛАУ со значением, прописанным в системе ЦОС Nomotex.
2. Проверка на то, что введенные студентом ответы являются ненулевыми и линейно независимыми для однородной системы.
3. Подстановка частного решения в исходную систему при заданном параметре λ и подстановка линейно независимых решений в однородную систему.
Аналогично описанным выше алгоритмам, данный также дает возможность оценивать в отдельности каждый этап решения задачи, и при автоматической проверке начислять баллы за каждый из этапов по отдельности, в данной задаче это реализовано следующим образом:
1. За верно найденный ранг матрицы студенту выставляется 0,3 балла от полного балла, предусмотренного при оценивании задачи.
2. За правильное значение параметра λ начисляется 0,2 балла. В данном пункте от студента требуется знание критерия Кронекера – Капелли.
3. За последний пункт, нахождение всех решений СЛАУ, начисляется остальная часть – 0,5 баллов.
Заключение
В работе представлены методы автоматической генерации, проверки и оценивания задач по теме системы линейных уравнений. Описанные алгоритмы позволяют генерировать условия задач таким образом, чтобы свести к минимуму возможность допустить арифметическую ошибку при нахождении решения системы уравнений. Методы автоматической проверки позволяют оценивать каждый этап решения и, что особенно важно при автоматизации, дать студенту обратную связь и указать на допущенные при решении ошибки.
Данные методы также могут быть применены в задачах, которые предусматривают решение системы линейных уравнений как один из этапов решения, например, нахождение собственных векторов, проверка на линейную зависимость и др.