science-review.ru
Повышение эффективности обучения математике в школе – насущная потребность отечественного образования, определяемая общей математизацией промышленности, экономики и социума в целом [1; 2]. Исходя из этого, автором была создана система «Живая математика», позволяющая существенно повысить эффективность обучения математике в школе [3]. Эта система основывается на принципах Искусственного Интеллекта в образовательном процессе [4]. «Живая математика» состоит из нескольких подсистем, объединенных единой идеологией. В статье представлен достаточно подробный разбор компонента «Графики» системы «Живая математика», предназначенный для графической иллюстрации решения задач школьной математики.
Необходимость такой подсистемы вытекает из следующих соображений. В большинстве алгебраических и тригонометрических задач (например, решение уравнений, задачи с параметрами, тригонометрические уравнения) удачно подобранная графическая иллюстрация позволяет выделить области, в которых следует искать решение, и число решений в зависимости от выбора параметров. Помимо этого, становится очевидным характер поведения функций, например увидеть асимптоты и области определения. Это существенно экономит время нахождения окончательного решения, т.к. позволяет исключать из рассмотрения области, заведомо не содержащие решений. Используя графики, легче исследовать поведение функций, например находить экстремумы, точки пересечения с осями, области определения и значений, асимптоты, влияние параметров на вид графика и пр. Помимо этого, графики часто наводят на мысль о направлении, в котором следует искать решение. Например, подсказывают такие свойства функции, как четность или нечетность, что полезно для установления единственности решения.
Чтобы владеть навыком образного мышления в алгебре и тригонометрии, необходимо уметь быстро строить графики функций, заданных явно или неявно, например характеристическими предикатами. Поэтому в системе «Живая математика» введена подсистема «Графики», как аппарат построения графиков функций, цель которого развить у школьника образное мышление, что полезно при решении практически любых алгебраических и тригонометрических задач.
Семейство функций, для которых можно строить графики, практически неограниченно, т.к. имеется механизм суперпозиции функций из базисных. В связи с этим у школьника накапливается опыт работы с нестандартными функциями, что существенно расширяет его приемы решения алгебраических и тригонометрических задач. А формируемое при этом образное мышление позволяет сразу увидеть возможные решения, исходя из вида функций. Такие навыки весьма востребованы не только школьниками. Они полезны, например, инженерам, проектирующим новые устройства, т.к. позволяют быстро отсеивать неверные гипотезы, точная проверка которых может занять много машинного времени.
Еще один эффект от использования подсистемы «Графики» состоит в том, что преподаватель сможет быстро провести исследование функции, например квадратного трехчлена ax + bx + c, в зависимости от параметров (здесь: a, b, c), или функции с несколькими модулями, продемонстрировать геометрический смысл производной и т.п. В результате эффективность образовательного процесса существенно возрастает по сравнению с традиционной подачей материала.
Помимо собственно графических средств, которые представляет подсистема «Графики», следует обратить внимание на взаимодействие двух подсистем: «Графики» и «Алгебраист» всей системы «Живая математика». Как показано далее, их совместное использование крайне полезно при решении, например, уравнений. Так как базисы обеих подсистем создавались из потребности решать алгебраические задачи, то их взаимодействие усиливает возможности каждой, и тем самым возрастает продуктивность изучения любых тем, имеющих алгебраический компонент. Например, при решении нестандартных уравнений можно изобразить график функции для установления числа корней, а затем использовать разложение на множители для понижения степени многочлена. Или при решении неравенств выделить наиболее подходящие для анализа интервалы изменения переменной. Такие приемы дают возможность быстро выбирать адекватные способы решений. Далее эти приемы будут проиллюстрированы конкретными примерами.
Подсистема «Графики» обладает еще одной функцией, которая полезна при исследовании поведения функций – это возможность изображать графики функций, заданных неявно. Например, при исследовании уравнений с параметрами часто приходится исследовать поведение произвольной функции и окружности. Окружность задается уравнением с двумя переменными, и для ее изображения в подсистеме имеется возможность задать ее центр и радиус.
Чтобы сделать статью компактной, не будем приводить скриншоты форм, участвующих в работе подсистемы «Графики». Вместо этого подробно проиллюстрируем ее возможности на примерах реальных задач, взятых из материалов для подготовки к ЕГЭ и олимпиадам по математике [5].
Работа с подсистемой «Графики». Головная форма подсистемы «Графики» ориентирована на самого широкого пользователя. Здесь не будем изображать скриншоты форм, но подробно пройдемся по функционалу подсистемы. Затем использование этого функционала проиллюстрируем при решении нескольких задач из олимпиадного сборника. Верхнее горизонтальное меню головной формы представляет группы команд, которые используются в подсистеме для построения графиков различных функций. Подробно это меню и содержащиеся в нем команды опишем ниже.
Самый левый пункт меню называется «Основные функции». После его вызова открывается выпадающее меню, в котором перечисляются все типы базисных функций школьного курса математики, изучаемые в разделе «Алгебра». Это суть шаблоны функций: линейные, квадратичные, кубические, гиперболы, дробно-рациональные и пр. Все шаблоны заданы в параметрическом виде, тем самым предоставляя универсальный аппарат их описания. Так, линейные функции представлены шаблоном Ax+B. Задавая значения параметров A и B, получаем различные функции. То же касается остальных функций, перечисленных в этом разделе. В последующем они используются как для построения графиков в зависимости от значений параметров, так и для конструирования суперпозиций функций. Последнее существенно расширяет используемый набор функций, делая его практически неограниченным.
Проиллюстрируем возможность построения графиков на примере квадратичной функции после выбора в выпадающем меню пункта Квадратичные функции. Для построения графика конкретного квадратного трехчлена совершаем следующие действия.
1. Из выпадающего меню Основные функции выбираем пункт Квадратичные функции.
2. Задаем значения параметров A, B, C в текстовых окнах, расположенных на головной форме.
3. По умолчанию область графика ограничена значениями: по x: [-10, 10], по y: [-10, 10]. Интервалы можно изменить в соответствующих окнах головной формы.
4. Выбираем пункт горизонтального меню Оси. В результате появляется поле для рисования графика, которое расчерчено вертикальными и горизонтальными линиями для большей наглядности графиков.
5. После задания параметров функции выбираем пункт горизонтального меню Графики → Базисные функции. В результате появляется график квадратного трехчлена, с заданными параметрами.
6. Тут же можно провести исследование графика, меняя значения параметров. В этом случае у школьника вырабатывается образное представление о поведении функции.
Аналогично создаются графики остальных функций, перечисленных в пунктах Основные функции и Тригонометрические функции горизонтального меню.
На одном полотне можно изобразить графики для нескольких различных функций, тем самым осуществляя совместное исследование функций, как разных, так и одного типа, но с разными параметрами. Это полезно, например, при подборе параметров функции так, чтобы она удовлетворяла определенным свойствам. Подобные задачи возникают при решении задач с параметрами. Зачастую удачно подобранный графический образ дает существенную подсказку, в каком направлении следует двигаться при поиске решения.
Однако возможности подсистемы «Графики» не исчерпываются только построением графиков для базисных функций. Дополнительно имеется возможность построения графиков функций, представляющих собой суперпозицию практически не ограниченного числа базисных функций. Для этого в горизонтальном меню на головной форме имеется пункт меню «Суперпозиция», по которому осуществляется переход на новую форму, созданную специально для формирования суперпозиций. На ней имеется горизонтальное меню с перечислением всех необходимых базисных функций и инструментов задания суперпозиций. Это суть сумма, разность, произведение и пр., которые образуют полный инструментарий для формирования суперпозиций. Построение суперпозиции сопровождается рекурсивным формированием дерева с единственным корнем, которому приписывается результирующая функция. Дерево отображает вложенность функций, что делает процесс создания суперпозиции наглядным. Дерево суперпозиции имеет не только иллюстративную функцию, оно представляет собой инструмент для создания окончательной функции. Это осуществляется выбором двойным щелчком вершины дерева, которой приписан параметр, и последующим выбором либо числового значения параметра, либо функции, которая участвует в дальнейшем построении суперпозиции. Так как на глубину дерева ограничений нет, то можно построить практически любую функцию из заданных базисных. После окончательного формирования искомой суперпозиции запускается формирование графика, который изображается на том же полотне, где изображаются графики базисных функций. Одновременно можно изображать графики нескольких функций, что удобно при их исследовании.
Например, в задаче: решить неравенство ||x2 – 3| x – 1| < x + 2, требуется провести исследование двух функций: ||x2 – 3| x – 1| и x + 2. Первая представляет собой суперпозицию нескольких функций, так как содержит два модуля и степень. Вторая принадлежит семейству базисных. Одновременное исследование их графиков позволяет исключить из рассмотрения области, в которых заведомо нет решения неравенства.
Примеры использования подсистем «Графики» и «Алгебраист». В этом разделе приведем несколько примеров, иллюстрирующих пользу от использования подсистем «Графики» и «Алгебраист» при решении различных задач.
Пример 1. Найти все значения a, при которых уравнение x2+ax+8=0 имеет два различных вещественных корня, лежащих строго между 0 и 3. Квадратный трехчлен представляет собой сумму трех функций: параболы x2, ветви которой направлены вверх, линейной с коэффициентом a и константы 8. Чтобы прикинуть, в каких интервалах следует искать значение параметра a, изобразим графики квадратного трехчлена для трех случаев, когда a > 0 (a = 5) и a < 0 (a = -5 и a = -6). Становится ясно, что положительное значение a не приводит к решению, и решение достигается при a из диапазона (-5, -6). Действительно, уменьшая параметр a, начиная с -5, парабола опускается вниз. Нас интересуют те значения a, при которых она дважды пересечет ось абсцисс, на интервале (0, 3).
Далее решение стандартное, вначале формулируем неравенство a2 – 32 > 0 (условие существования двух корней), и второе неравенство вытекает из требования, что значение квадратного трехчлена в точке x = 3 больше нуля: 32 + 3a + 8 > 0. Из первого неравенства (в соответствии с подсказкой, что a < 0) следует, что a < -4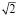
, из второго a > -17/3.
Польза от использования подсистемы «Графики» при решении этого уравнения состоит в том, что из графических соображений становится понятным, в каком интервале должен располагаться параметр a. Таким образом, исключается излишняя работа по исследованию других интервалов.
Пример 2. Решить уравнение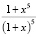 
= 31.
Вначале проанализируем графики функций, стоящих в числителе и знаменателе. Из графиков видно, что решение не может быть положительным, т.к. знаменатель больше числителя в положительной полуплоскости. Следовательно, решение – отрицательное. Теперь одно решение легко найти подбором: x = -2. Но могут быть и еще решения. Для того чтобы их найти, проведем анализ функции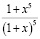 
, для чего построим ее график на интервале [-5, 1]. График состоит из двух ветвей и обладает вертикальной асимптотой, возникающей из-за неопределенности в точке x = -1. Как видно, это уравнение имеет два решения. Их легко угадать, это x = -2, -1/2. Проверкой убеждаемся, что они подходят. Теперь докажем это аналитически. Для этого, используя подсистемы «Алгебраист», разделим 1 + x5 на 1 + x. Частное от деления есть x4 – x3 + x2 – x + 1.
В результате получаем уравнение 31(1+x)4 = x4 – x3 + x2 – x + 1. Возведение 1+x в четвертую степень с помощью «Алгебраиста» сводит исходное уравнение к уравнению 31x4 + 124x3 + 186x2 + 124x + 31 = = x4 – x3 + x2 – x + 1, что равносильно уравнению 30x4 + 125x3 + 185x2 + 125x + 30 = 0. Далее, используя «Алгебраист», раскладываем на множители левую часть 30x4 + 125x3 + +185x2 + 125x + 30 и получаем произведение (x + 2)(30x3 + 65x2 + 55x + 15). Следовательно, первый корень x = -2 нами подтвержден. После сокращения оставшегося выражения получаем уравнение 6x3 + 13x2 + 11x + 3 = 0. Для левой функции строим график на интервале [-1, 1]. Второй корень x = – 1/2 без труда обнаруживается из графики. Проверяем подстановкой и убеждаемся, что это верно. Таким образом, только графическими средствами мы решили задачу, получив два точных корня. Из вида графика следует, что третьего корня нет.
С другой стороны, система «Алгебраист» дает возможность то же найти аналитически, не прибегая к сложным преобразованиям, выполняемым вручную. Для этого делим уравнение 6x3 + 13x2 + 11x + 3 = 0 на x3 и производим замену y = 1/x. В результате получаем уравнение 3y3 + 11y2 + 13y + 6 = 0. Используем «Алгебраист» и раскладываем левое выражение. Получаем уравнение (y + 2)(3y2 + 5y + 3) = 0. Отсюда уже аналитически следует, что второй корень равен -1/2. Уравнение 3y2 + 5y + 3 = 0 корней не имеет.
Польза от использования двух подсистем «Графики» и «Алгебраист» при решении этого примера состоит в том, что наглядно выделяются интервалы, в которых лежат решения, и сами эти решения. Далее задача сводится не к нахождению решений, а к обоснованию, что они имеют такие значения. Это существенно проще, нежели выполнять все аналитические преобразования. Следует заметить, что в этом примере строилась сложная функция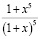 
, с использованием механизма построения суперпозиции.
Пример 3. Решить неравенство
|x2 – 3|x – 1|| < x + 2.
В этом примере также используется механизм построения суперпозиции для определения функции слева. Правая функция – линейная и принадлежит базисным. Строим графики обеих функций, расположенных слева и справа от знака неравенства. График функции |x2 – 3|x – 1|| состоит из нескольких частей. Правая ветвь определяется функцией x2 – 3(x – 1) = x2 – 3x + 3. Средняя часть – двумя функциями: -(x2 – 3(x – 1)) и -(x2 + 3(x – 1)). Функции неравенства имеют две точки пересечения в левой ветви и в средней части. Нас интересует вторая функция. Остается решить два уравнения: –(x2 + 3(x – 1)) = x +2 и x2 – 3x + 3 = x +2. Решая их, получаем искомый интервал (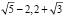
).
Достоинство графического метода при решении этого примера состоит в том, что он позволяет отбросить заведомо не подходящие варианты. В результате экономятся ресурсы, что немаловажно, например, для подготовки к экзаменам или олимпиадам. Внимание ученика сосредоточивается именно на том интервале, где лежит решение, что избавляет его от необходимости исследовать варианты, заканчивающиеся констатацией: на этом интервале решения нет.
Пример 4. При каких значениях a неравенство -1 ≤ sin x (a – cos 2x) ≤ 1 выполняется при любом x.
Здесь уместно упомянуть, что в системе «Живая математика» имеется весьма мощный банк различной справочной информации по школьной математике. Эта справочная информация сосредоточена в разделе «Справка» и содержит не только полезные соотношения из всех разделов школьной математики, но и большое число полезных приемов решения задач, разбитых по разделам: арифметика, алгебра, геометрия, тригонометрия и пр.
Для решения исходной задачи воспользуемся равенством cos 2x = 1 – 2sin2 x, которое легко находим в «Справке», и получаем неравенства: -1 ≤ sin x (a – 1 + 2sin2 x) ≤ 1. Используя замену y = sin x и A = a – 1, перейдем к неравенствам -1 ≤ y (2y2 + A) ≤ 1. Здесь диапазон изменения y ∈ [-1, 1]. Далее с помощью «Алгебраиста» выполним умножение одночлена на многочлен и получим неравенства -1 ≤ 2y3 + Ay ≤ 1. Для простоты вводим обозначение f(y) = 2y3 + Ay. Графики для функции f показывают, что при A ≥ 0 решения нет. Все они имеют единственную точку пересечения с осью абсцисс в точке x = 0. При A < 0 графики этой функции ведут себя сложнее, у них кроме точки x = 0, имеются и еще по две точки пересечения, одна на положительной, другая – на отрицательной полуоси. Так как y ∈ [-1, 1], то строим графики этой функции на интервале [-2, 2], чтобы увидеть общее поведение. Из графиков видно, что на интервале [-1, 0] функция имеет положительный экстремум, а на интервале [0, 1] – отрицательный. Из вида функции на диапазоне [-1, 1] и в силу симметрии вытекает, что функцию f можно исследовать только на одном диапазоне [0, 1] изменения аргумента. На интервале [-1, 0] решение находится из соображений симметрии, что следует из вида графиков. Из графиков при различных значениях параметра A следует, что надо провести полноценное исследование поведения функции на интервале [0, 1]. Т.е. оценить экстремум и значение в граничной точке x = 1. Эти значения не должны быть меньше -1. Провести исследование функции, когда имеется ее график, не представляет труда. Поэтому решение исходных неравенств сведено к исследованию простой функции. И существенную роль при этом сыграло графическое сопровождение процесса решения.
Достоинство использования в этом примере подсистемы «Графики» по сравнению с «ручным» решением состоит в том, что весь процесс сопровождается содержательными иллюстрациями в виде графиков. Таким образом, мы оперируем формальными конструкциями, одновременно привлекая их содержательный смысл.
Вывод
В статье приведено относительно подробное изложение подсистемы «Графики» системы «Живая математика», назначение которой состоит в графической иллюстрации поведения функций, изучаемых в школьной математике. Показано, что можно строить графики как для базисных функций, так и для функций, получаемых суперпозицией из базисных. Продемонстрировано, что использование подсистем «Графики» и «Алгебраист» позволяет повысить эффективность обучения школьников навыкам решения алгебраических задач.