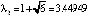Математическая модель  объекта, процесса или явления может представлять собой функцию или систему функций, уравнение или их систему. Уравнения могут быть конечными (например, алгебраическими или трансцендентными), дифференциальными, интегральными, рекуррентными и др. Процессы можно описывать дискретно – итерациями отображений, либо непрерывно – траекториями дифференциальных уравнений или интегральными кривыми. Пусть модель
объекта, процесса или явления может представлять собой функцию или систему функций, уравнение или их систему. Уравнения могут быть конечными (например, алгебраическими или трансцендентными), дифференциальными, интегральными, рекуррентными и др. Процессы можно описывать дискретно – итерациями отображений, либо непрерывно – траекториями дифференциальных уравнений или интегральными кривыми. Пусть модель  зависит от некоторого параметра λ:
зависит от некоторого параметра λ:  . Значение параметра λ* называется бифуркационным, если при переходе через него объект изменяет качественные или количественные характеристики [1–3]. Поясним сказанное простыми примерами.
. Значение параметра λ* называется бифуркационным, если при переходе через него объект изменяет качественные или количественные характеристики [1–3]. Поясним сказанное простыми примерами.
Пример. Рассмотрим модель 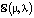 :
: 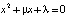 , с двумя параметрами
, с двумя параметрами 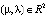 , т.е. семейство квадратных уравнений. Таким образом, устанавливается биекция между точками плоскости параметров R2 и множеством квадратных уравнений. На плоскости параметров рассмотрим три множества
, т.е. семейство квадратных уравнений. Таким образом, устанавливается биекция между точками плоскости параметров R2 и множеством квадратных уравнений. На плоскости параметров рассмотрим три множества 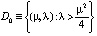 ,
, 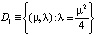 ,
, 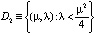 . Ясно, что для точек из множества D0 чисел, которые представляют решения квадратного уравнения на вещественной оси R, нет. Как только точка (μ, λ) оказывается на параболе D1, уравнение приобретает решение
. Ясно, что для точек из множества D0 чисел, которые представляют решения квадратного уравнения на вещественной оси R, нет. Как только точка (μ, λ) оказывается на параболе D1, уравнение приобретает решение 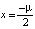 . При переходе точки (μ, λ) в область D2 решение
. При переходе точки (μ, λ) в область D2 решение 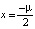 расщепляется на два
расщепляется на два 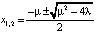 , т.е. происходит бифуркация (ветвление), при этом кривую D1 естественно называть бифуркационной кривой.
, т.е. происходит бифуркация (ветвление), при этом кривую D1 естественно называть бифуркационной кривой.
Пример. Рассмотрим семейство алгебраических уравнений 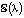 :
: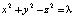 . Хорошо известно, что при λ = 0 уравнение определяет конус, при λ > 0 – однополостный гиперболоид, при λ < 0 – двуполостный гиперболоид, т.е. при переходе через λ = 0 геометрический объект изменяет качество. Стало быть, значение параметра λ = 0 – бифуркационное.
. Хорошо известно, что при λ = 0 уравнение определяет конус, при λ > 0 – однополостный гиперболоид, при λ < 0 – двуполостный гиперболоид, т.е. при переходе через λ = 0 геометрический объект изменяет качество. Стало быть, значение параметра λ = 0 – бифуркационное.
Целью статьи является построение методики изложения начала качественного исследования двух динамических моделей c непрерывным и дискретным временем
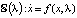 ,
,
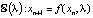
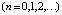
Несмотря на внешнюю схожесть и простоту этих моделей, вторая – оказывается труднее в исследовании, существенно содержательней и несравнимо богаче эффектами. Заметим, что в стандартных курсах дифференциальных уравнений втузов эти вопросы часто не затрагиваются. Однако в настоящее время этот материал желательно включить в программы для первого знакомства. Используемый в статье математический аппарат несложен, и мы не исключаем возможность ознакомления с ним школьников старших классов, например в рамках факультатива, учитывая, что качественные методы исследования, вычислительный эксперимент, имитационное моделирование играют в настоящее время в науке огромную роль [3; 4].
Динамические системы с непрерывным временем
Определение 1. Динамической или автономной системой на прямой называется уравнение
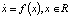 . (1)
. (1)
Здесь x = x(t), t – время, f – непрерывная функция x; 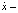 производная по t, т.е. скорость.
производная по t, т.е. скорость.
Уравнение (1) задает закон движения точки (изображающей точки) по прямой 0x, называемой фазовой или прямой состояний. Точки 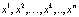 в которых f(x) = 0 называются положениями равновесия – это простейшие траектории. Интервалы
в которых f(x) = 0 называются положениями равновесия – это простейшие траектории. Интервалы 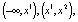 …,
…, 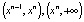 отвечают также траекториям, по ним точки движутся либо к положениям равновесия, либо от них, либо убегают на бесконечность. Направление движения точек указывается стрелкой. При этом работает правило: если f(x) > 0 при
отвечают также траекториям, по ним точки движутся либо к положениям равновесия, либо от них, либо убегают на бесконечность. Направление движения точек указывается стрелкой. При этом работает правило: если f(x) > 0 при 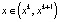 , то стрелка на интервале ставится вправо, если f(x) < 0 при
, то стрелка на интервале ставится вправо, если f(x) < 0 при 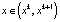 , то влево. Таким образом, фазовая прямая разбивается на траектории: положения равновесия и ориентированные интервалы. Других траекторий в этом случае нет. Заметим, что если
, то влево. Таким образом, фазовая прямая разбивается на траектории: положения равновесия и ориентированные интервалы. Других траекторий в этом случае нет. Заметим, что если 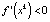 , то интервал
, то интервал 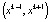 будет представлять собой область притяжения точки xk, т.е. окружающие его точки будут стремиться к нему. Такие положения равновесия называются устойчивыми или притягивающими. Если
будет представлять собой область притяжения точки xk, т.е. окружающие его точки будут стремиться к нему. Такие положения равновесия называются устойчивыми или притягивающими. Если 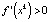 , то – неустойчивыми или отталкивающими. Таким образом, неравенства
, то – неустойчивыми или отталкивающими. Таким образом, неравенства 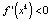 и
и 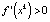 выступают критериями устойчивости (неустойчивости) положений равновесия. Задача разбиения оси 0x на траектории – задача качественного исследования уравнения (1). Обращаем внимание, что мы не прибегали к операции интегрирования, и вообще, качественное исследование подразумевает изучение свойств решений (траекторий) по структуре уравнения [2; 5]. Следующий пример прояснит сказанное.
выступают критериями устойчивости (неустойчивости) положений равновесия. Задача разбиения оси 0x на траектории – задача качественного исследования уравнения (1). Обращаем внимание, что мы не прибегали к операции интегрирования, и вообще, качественное исследование подразумевает изучение свойств решений (траекторий) по структуре уравнения [2; 5]. Следующий пример прояснит сказанное.
Пример 1. Рассмотрим уравнение
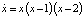 . (2)
. (2)
Ясно, что 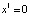 ,
, 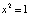 ,
, 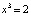 – его положения равновесия. Из графика функции
– его положения равновесия. Из графика функции 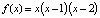 (рис. 1) легко заключить, что
(рис. 1) легко заключить, что
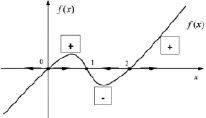
Рис. 1. Фазовая прямая 0x и семь траекторий на ней
x1 = 0, x3 = 2 – неустойчивые положения равновесия (иначе они называются седловыми), x2 = 1 – устойчивое (узловое), причем интервал (0,2) является его областью притяжения. Обратим внимание на неравенства в положениях равновесия 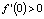 ,
, 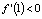 ,
, 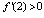 .
.
Бифуркации в системах с непрерывным временем
Рассмотрим теперь уравнение с параме- тром
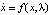 (3)
(3)
и поставим вопрос: как структура фазовой прямой будет меняться при изменении λ. Понятие бифуркации, обсуждаемое далее, продемонстрируем на следующем примере.
Пример 2. Рассмотрим некоторое обобщение уравнения (2)
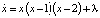 . (4)
. (4)
Так как параметр λ определяет сдвиг графика функции y = f(x, λ) вдоль оси ординат, то уравнение f(x, λ) = 0 может иметь разное количество корней. Следовательно, количество положений равновесия уравнения (4) зависит от λ. Нетрудно проверить, что при 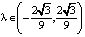 их будет три, при
их будет три, при 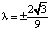 – два, а при
– два, а при 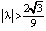 – одно.
– одно.
В данном примере изменения на фазовой прямой связаны с появлением (исчезновением) положения равновесия, при этом говорят о бифуркации рождения (гибели) положения равновесия. При этом бифуркационными значениями будут 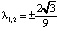 . Обратим внимание, что при
. Обратим внимание, что при 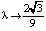 устойчивое и неустойчивое положения равновесия сливаются, образуя, как говорят, седло-узел (или полуустойчивое положение равновесия) (рис. 2). Аналогичная картина наблюдается и при
устойчивое и неустойчивое положения равновесия сливаются, образуя, как говорят, седло-узел (или полуустойчивое положение равновесия) (рис. 2). Аналогичная картина наблюдается и при 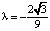 (почему?).
(почему?).
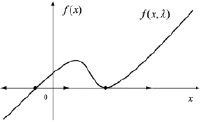
Рис. 2. Неустойчивый узел и седло-узел при 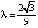
Дискретные динамические системы и их траектории
Представим теперь для определенности некоторый объект (возможно процесс), состояние которого в каждый дискретный момент времени t = k определяется величиной xk = x(k). Предположим, что состояние xk в момент времени t = k полностью определяет состояние 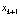 в последующий момент времени t = k + 1 по формуле
в последующий момент времени t = k + 1 по формуле
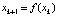 . (5)
. (5)
Здесь f – заданная функция (иначе – отображение), определенная на множестве 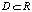 .
.
Определение 2. Уравнение (5), представляющее собой рекуррентную формулу первого порядка для получения итерационной последовательности, называется дискретной динамической системой с одномерным фазовым пространством.
Заметим, что численные методы решения уравнений 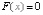 или
или 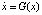 , основанные на идее дискретизации, также приводят к уравнениям вида (5) [5; 6] (почему?).
, основанные на идее дискретизации, также приводят к уравнениям вида (5) [5; 6] (почему?).
Определение 3. Пусть x0 – заданное число. По формуле (5) построим последовательность
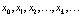 (6)
(6)
Такую последовательность называют решением, а соответствующее множество точек на оси 0x – траекторией системы (5), выпущенной из точки x0. Впрочем, в дальнейшем решение (6) мы будем интерпретировать с геометрической точки зрения, т.е. как совокупность точек на прямой, и отождествлять его, таким образом, с траекторией.
Центральным вопросом в исследовании эволюции динамических систем является вопрос о финитном поведении. Иными словами: как ведут себя траектории при 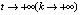 и что представляют собой предельные множества. Оказывается, что в отличие от непрерывных одномерных систем, в которых эволюция конкретной начальной точки заканчивается либо в положении равновесия, либо на бесконечности, структура предельных множеств в дискретных системах вида (5) может быть существенно сложнее. Это мы увидим позднее, а сейчас обратимся к следующему примеру.
и что представляют собой предельные множества. Оказывается, что в отличие от непрерывных одномерных систем, в которых эволюция конкретной начальной точки заканчивается либо в положении равновесия, либо на бесконечности, структура предельных множеств в дискретных системах вида (5) может быть существенно сложнее. Это мы увидим позднее, а сейчас обратимся к следующему примеру.
Пример 3. Рассмотрим систему (5), где 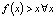 . Ясно, что для любой точки x0 соответствующая траектория
. Ясно, что для любой точки x0 соответствующая траектория 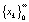 будет монотонно возрастающей:
будет монотонно возрастающей: 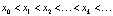 и стремиться при k → +∞ к бесконечности. Это наглядно демонстрирует так называемая диаграмма Кёнигса-Ламерея, принцип построения которой описан на рис. 3.
и стремиться при k → +∞ к бесконечности. Это наглядно демонстрирует так называемая диаграмма Кёнигса-Ламерея, принцип построения которой описан на рис. 3.
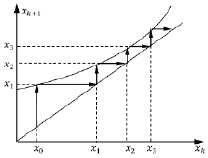
Рис. 3. Убегающая в бесконечность траектория (положений равновесия нет)
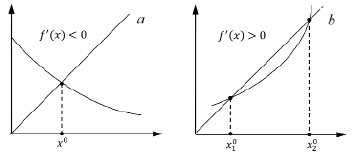
Рис. 4. Положения равновесия
Ясно, что если 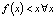 , то для любой начальной точки
, то для любой начальной точки 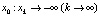 . Нарисуйте самостоятельно диаграмму в этом случае.
. Нарисуйте самостоятельно диаграмму в этом случае.
Определение 4. Предположим теперь, что 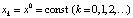 является решением (5). Такое решение называется стационарным, а соответствующая траектория, т.е. точка x0 на оси 0x – положением равновесия.
является решением (5). Такое решение называется стационарным, а соответствующая траектория, т.е. точка x0 на оси 0x – положением равновесия.
Положения равновесия системы (5) находятся из уравнения 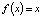 , корни которого суть абсциссы точек пересечения двух графиков
, корни которого суть абсциссы точек пересечения двух графиков 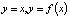 (рис. 4).
(рис. 4).
Замечание. Легко видеть, что если система задана монотонно убывающим отображением f, то в ней возможно лишь одно положение равновесия (рис. 4а). В случае монотонно возрастающего отображения f возможно несколько (рис. 4в).
В дискретной системе, заданной монотонно возрастающим отображением, можно наблюдать и простейший тип бифуркации – бифуркацию рождения нового положения равновесия. Этот тип бифуркации, так же как и в непрерывном случае, поясним на примере.
Пример 4. Рассмотрим систему 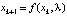 , где
, где 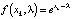 . Видно, что при λ < 1 – положений равновесия нет, при λ > 1 – два, а при λ = 1 – одно (рис. 5), т.е. параметр λ = 1 – бифуркационный.
. Видно, что при λ < 1 – положений равновесия нет, при λ > 1 – два, а при λ = 1 – одно (рис. 5), т.е. параметр λ = 1 – бифуркационный.
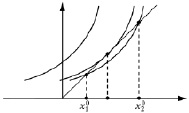
Рис. 5. Бифуркация положений равновесия
Определение 5. Предположим теперь, что система (5) имеет решение
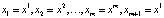 ,…,
,…,
причем никакие два числа в наборе 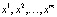 не совпадают. Такое решение называется периодическим, число m – периодом, а соответствующая траектория – циклом периода m. Числа
не совпадают. Такое решение называется периодическим, число m – периодом, а соответствующая траектория – циклом периода m. Числа 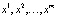 называют периодическими точками периода m отображения f.
называют периодическими точками периода m отображения f.
Цикл периода m будем обозначать символом 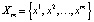 .
.
Договоримся также о следующем обозначении: 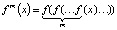 .
.
Тогда нетрудно проверить, что для периодических точек периода m цикла Xm имеет место m равенств: 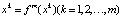 . Заметим, что цикл периода m = 1 представляет собой положение равновесия. Для нахождения цикла
. Заметим, что цикл периода m = 1 представляет собой положение равновесия. Для нахождения цикла 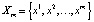 достаточно найти одну периодическую точку x1 периода m отображения f:
достаточно найти одну периодическую точку x1 периода m отображения f:
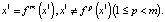 (7)
(7)
Другие компоненты периодической траектории найдутся по формулам
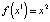 ,
, 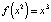 , …,
, …, 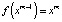 .
.
Замечание. Пусть f – непрерывное отображение и для некоторых чисел 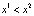 выполняется
выполняется 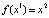 ,
, 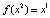 . Это означает, что
. Это означает, что 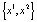 – цикл периода 2. Ясно также, что точки
– цикл периода 2. Ясно также, что точки 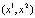 и
и 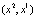 расположены симметрично относительно биссектрисы y = x. В силу непрерывности f вытекает, что существует точка
расположены симметрично относительно биссектрисы y = x. В силу непрерывности f вытекает, что существует точка 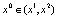 , для которой
, для которой 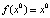 , т.е. x0 – положение равновесия. Таким образом, из существования цикла периода 2 следует существование положения равновесия.
, т.е. x0 – положение равновесия. Таким образом, из существования цикла периода 2 следует существование положения равновесия.
Пример 5. На множестве (2, +∞) рассмотрим 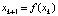 , где
, где 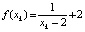 . Видно, что
. Видно, что 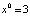 – положение равновесия, а f – убывающая. Кроме того, для любого x > 2 выполняется
– положение равновесия, а f – убывающая. Кроме того, для любого x > 2 выполняется 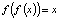 . Последнее соотношение означает, что все траектории рассматриваемой системы – циклы периода два. Такую систему можно назвать консервативной (почему?).
. Последнее соотношение означает, что все траектории рассматриваемой системы – циклы периода два. Такую систему можно назвать консервативной (почему?).
В заключение этого пункта отметим, что дискретные системы, задаваемые монотонно возрастающими отображениями, подобны непрерывным динамическим системам. В них отсутствуют периодические траектории. В противоположность этому, как мы это видели в примере 5, в дискретных системах, заданных монотонно убывающими отображениями, можно наблюдать новый тип траекторий, а именно, периодические. Кроме того, можно наблюдать и новый тип бифуркации – бифуркацию рождения цикла. Это мы увидим ниже.
Устойчивость положений равновесия и циклов
Пусть x0 – положение равновесия (5): 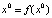 .
.
Определение 6. Положение равновесия x0 называется устойчивым, если существует окрестность (α, β) точки x0 такая, что для любой начальной точки 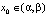 выполняется
выполняется 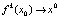 при k → +∞. Если, кроме того,
при k → +∞. Если, кроме того, 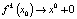 при
при 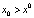 и
и 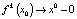 при
при 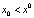 , то x0 называется устойчивым узлом. Если же
, то x0 называется устойчивым узлом. Если же 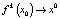 и
и 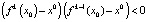 , то называется устойчивым фокусом. При этом интервал (α, β) называют областью притяжения устойчивого положения равновесия x0. Если интервал
, то называется устойчивым фокусом. При этом интервал (α, β) называют областью притяжения устойчивого положения равновесия x0. Если интервал 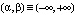 , то систему (5) называют устойчивой в целом.
, то систему (5) называют устойчивой в целом.
Определение 7. Положение равновесия x0 называется неустойчивым, если любая траектория, выпущенная из сколь угодно малой окрестности 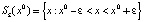 , за конечное время (конечное число шагов) покидает
, за конечное время (конечное число шагов) покидает 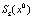 .
.
Критерии устойчивости и неустойчивости положений равновесия
Если для отображения f системы (5) выполняется неравенство 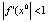 , то положение равновесия x0 – устойчиво. На рис. 6 a изображен устойчивый узел, на рис. 6 b – устойчивый фокус. Если для отображения f системы (5) выполняется неравенство
, то положение равновесия x0 – устойчиво. На рис. 6 a изображен устойчивый узел, на рис. 6 b – устойчивый фокус. Если для отображения f системы (5) выполняется неравенство 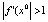 , то положение равновесия x0 – неустойчиво. На рис. 7 a, b изображены соответственно неустойчивый узел и неустойчивый фокус.
, то положение равновесия x0 – неустойчиво. На рис. 7 a, b изображены соответственно неустойчивый узел и неустойчивый фокус.
На рис. 8, 9 изображены графики монотонно возрастающих отображений f, порождающих дискретные системы с тремя положениями равновесия. Обратим внимание на то, что граничными точками области притяжения устойчивого положения равновесия являются неустойчивые положения равновесия.
Рис. 6. Устойчивые узел и фокус
Рис. 7. Неустойчивые положения равновесия
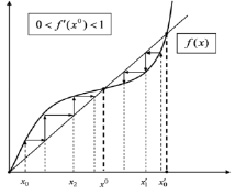
Рис. 8. x0 – устойчивое положение равновесия
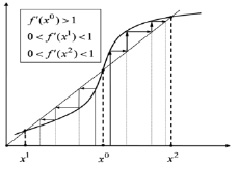
Рис. 9. x0 – неустойчивое положение равновесия
Рассмотрим теперь цикл 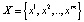 периода m системы (5). Напомним, что все числа, образующие цикл, различны (в противном случае мы имели бы цикл меньшего периода).
периода m системы (5). Напомним, что все числа, образующие цикл, различны (в противном случае мы имели бы цикл меньшего периода).
Определение 8. Цикл X называется устойчивым (притягивающим), если существует окрестность S этого цикла такая, что для любой точки 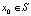 траектория
траектория 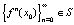 расщепляется на m последовательностей, сходящихся к точкам
расщепляется на m последовательностей, сходящихся к точкам 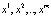 . При этом максимальная окрестность S, точки которой обладают указанным свойством, называется областью притяжения цикла X [6; 7].
. При этом максимальная окрестность S, точки которой обладают указанным свойством, называется областью притяжения цикла X [6; 7].
Так, например, для устойчивого цикла 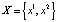 периода 2 с областью притяжения S в зависимости от выбора x0 может быть (рис. 10)
периода 2 с областью притяжения S в зависимости от выбора x0 может быть (рис. 10)
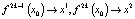 либо
либо 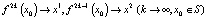
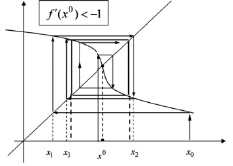
Рис. 10. Диаграмма Кенигса-Ламерея для устойчивого цикла
Напомним, что числа x1, x2 связаны формулами f(x1) = x2, f(x2) = x1.
Критерий устойчивости цикла периода два
Рассмотрим уравнение 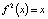 , корнями которого являются x1, x2, и найдем производную отображения
, корнями которого являются x1, x2, и найдем производную отображения 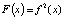 :
: 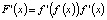 . Учитывая, что
. Учитывая, что 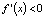 , получим
, получим 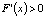 . А это означает, что отображение
. А это означает, что отображение 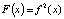 – монотонно возрастающее. Далее возможна альтернатива, отмеченная на рис. 11.
– монотонно возрастающее. Далее возможна альтернатива, отмеченная на рис. 11.
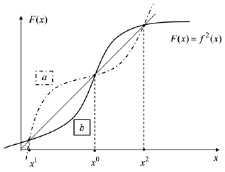
Рис. 11. Пунктирной кривой отмечен неустойчивый цикл, сплошной – устойчивый
Для формулировки критерия введем определение.
Определение 9. Мультипликатором цикла 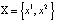 называется
называется 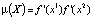 .
.
Из сказанного и определения 10 вытекает критерий: цикл X является устойчивым, если 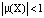 , и неустойчивым, если
, и неустойчивым, если 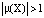 .
.
Пример 6. Рассмотрим систему 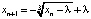 , где λ – параметр. Нетрудно видеть, что правая часть
, где λ – параметр. Нетрудно видеть, что правая часть 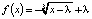 является монотонно убывающей на всей вещественной оси и, кроме того,
является монотонно убывающей на всей вещественной оси и, кроме того, 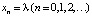 является неустойчивым стационарным решением. Стало быть, x0 = λ положение равновесия. Найдем периодическую траекторию системы. Для этого рассмотрим уравнение
является неустойчивым стационарным решением. Стало быть, x0 = λ положение равновесия. Найдем периодическую траекторию системы. Для этого рассмотрим уравнение 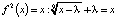 . Откуда легко находятся корни x0 = λ и
. Откуда легко находятся корни x0 = λ и 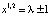 – периодические точки периода 2 и цикл
– периодические точки периода 2 и цикл 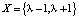 . Исследуем цикл на устойчивость. Для этого вычислим производную
. Исследуем цикл на устойчивость. Для этого вычислим производную 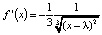 , её значения
, её значения 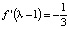 ,
, 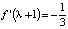 и мультипликатор
и мультипликатор 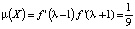 . Учитывая неравенство
. Учитывая неравенство 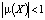 и критерий устойчивости, заключаем, что цикл
и критерий устойчивости, заключаем, что цикл 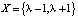 является устойчивым.
является устойчивым.
Введенное понятие мультипликатора распространяется и на произвольную периодическую траекторию 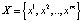 . А именно: мультипликатором цикла X называется число
. А именно: мультипликатором цикла X называется число 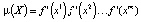 . При этом остается в силе и указанный выше критерий: если
. При этом остается в силе и указанный выше критерий: если 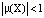 , то цикл X устойчив, если
, то цикл X устойчив, если 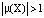 , то – неустойчив.
, то – неустойчив.
Итак, в дискретных системах с одномерным фазовым пространством, заданных монотонными отображениями, могут наблюдаться траектории трех типов. Это положения равновесия, периодические траектории, т.е. циклы и траектории, асимптотически стремящиеся при n → +∞ либо к положениям равновесия, либо к циклам, либо уходящие на бесконечность. По существующей терминологии устойчивые положения равновесия и циклы называют аттракторами (регулярными аттракторами) [3; 4; 6].
Дискретная система, заданная треугольным отображением
В системах, заданных немонотонными отображениями f, может наблюдаться еще один тип траекторий. Этот тип связывают с фактом открытия в некоторых простых системах сложного установившегося динамического поведения. К настоящему времени уже известно множество примеров детерминированных динамических систем, в которых траектории ведут себя хаотическим, т.е. непредсказуемым образом [4; 7; 8]. Это явление называют детерминированным хаосом [6; 7]. Значимость этого открытия, сделанного в конце XX века, невозможно переоценить. Оно позволяет по-новому взглянуть на многие явления окружающего нас мира и переосмыслить наши знания о нем.
Не имея возможности дать сколько-нибудь полное изложение вопросов, связанных с теорией детерминированного хаоса, мы ограничимся демонстрацией и обсуждением двух важных примеров систем, в которых наблюдается сложное поведение траекторий. При этом обратим внимание на основные черты, которыми обладают динамические системы, порождающие хаотическую динамику и сценарии возникновения хаоса.
Начнем с примера 
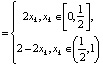 (рис. 12).
(рис. 12).
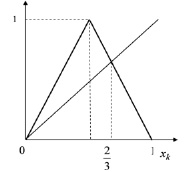
Рис. 12. График треугольного отображения
Видно, что функция f (треугольное отображение) задана на замкнутом промежутке [0,1] и отображает отрезок [0,1] в себя: 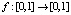 . Таким образом, траектории, начавшиеся в отрезке [0,1], никогда в дальнейшем не покидают его. Кроме того, легко находятся две простейшие траектории. Это положения равновесия
. Таким образом, траектории, начавшиеся в отрезке [0,1], никогда в дальнейшем не покидают его. Кроме того, легко находятся две простейшие траектории. Это положения равновесия 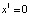 и
и 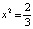 . Учитывая неравенства
. Учитывая неравенства 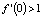 ,
, 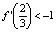 , заключаем, что оба положения равновесия неустойчивы. Из очевидного тождества
, заключаем, что оба положения равновесия неустойчивы. Из очевидного тождества 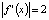 для всех
для всех 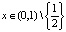 следует, что траектории, выпущенные из двух сколь угодно близких начальных точек
следует, что траектории, выпущенные из двух сколь угодно близких начальных точек 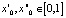 , экспоненциально разбегаются друг от друга, оставаясь в пределах интервала [0,1]. Это свойство траекторий называют чувствительностью к начальным данным (экспоненциальной неустойчивостью траекторий). На рис. 13 представлена одна траектория, выпущенная из точки x0. Для того чтобы ощутить явление неустойчивости, возьмите в качестве начальной точку, близкую к x0, и постройте соответствующую ей траекторию, используя диаграмму Кенигса-Ламерея.
, экспоненциально разбегаются друг от друга, оставаясь в пределах интервала [0,1]. Это свойство траекторий называют чувствительностью к начальным данным (экспоненциальной неустойчивостью траекторий). На рис. 13 представлена одна траектория, выпущенная из точки x0. Для того чтобы ощутить явление неустойчивости, возьмите в качестве начальной точку, близкую к x0, и постройте соответствующую ей траекторию, используя диаграмму Кенигса-Ламерея.
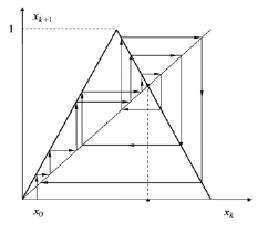
Рис. 13. Траектория, выпущенная из точки x0
Проведенные рассуждения наводят на мысль, что хаотические траектории, вероятно, возникают в системах, задаваемых растягивающими немонотонными отображениями 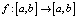 . Оказывается, что это действительно так. На первый взгляд может показаться, что все траектории в нашей системе непериодические. Однако это не верно. Более того, в рассматриваемой системе, как мы увидим, существуют циклы любого сколь угодно большого периода. Однако все они, повторяем, неустойчивы.
. Оказывается, что это действительно так. На первый взгляд может показаться, что все траектории в нашей системе непериодические. Однако это не верно. Более того, в рассматриваемой системе, как мы увидим, существуют циклы любого сколь угодно большого периода. Однако все они, повторяем, неустойчивы.
Легко видеть, например, что имеется один цикл периода 2: 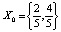 . Числа
. Числа 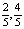 (периодические точки периода 2) – корни уравнения
(периодические точки периода 2) – корни уравнения 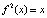 , для нахождения которых мы применили графический способ (рис. 14). Два цикла периода 3:
, для нахождения которых мы применили графический способ (рис. 14). Два цикла периода 3: 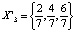 и
и 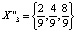 . Числа
. Числа 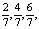
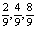 (периодические точки периода 3) – корни уравнения
(периодические точки периода 3) – корни уравнения 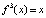 .
.
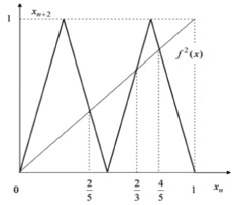
Рис. 14. График отображения f 2(x)
Пусть 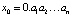 – десятичная конечная дробь. Ясно, что каждое
– десятичная конечная дробь. Ясно, что каждое 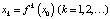 в силу специфики отображения f будет содержать не более n цифр после десятичной запятой. Всего же различных чисел вида 0. a1a2...an может быть 10n. Отсюда вытекает, что для выбранного x0 найдется номер
в силу специфики отображения f будет содержать не более n цифр после десятичной запятой. Всего же различных чисел вида 0. a1a2...an может быть 10n. Отсюда вытекает, что для выбранного x0 найдется номер 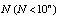 такой, что
такой, что 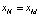 , где
, где 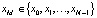 . А это будет означать, что траектория за конечное число шагов выходит на цикл
. А это будет означать, что траектория за конечное число шагов выходит на цикл 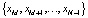 . Пусть теперь
. Пусть теперь 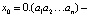 периодическая десятичная дробь. Тогда, как хорошо известно, найдутся натуральные числа s и
периодическая десятичная дробь. Тогда, как хорошо известно, найдутся натуральные числа s и 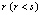 , такие, что
, такие, что 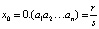 . Ясно также, что все последующие числа xk траектории будут представляться дробями вида
. Ясно также, что все последующие числа xk траектории будут представляться дробями вида 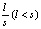 , что в свою очередь также приведет к периодической траектории. Если же в качестве x0 взять иррациональное число, десятичная запись которого представляет собой бесконечную непериодическую дробь, то эффекта повторяемости уже не будет, т.е. мы будем наблюдать непериодическую (хаотическую) траекторию.
, что в свою очередь также приведет к периодической траектории. Если же в качестве x0 взять иррациональное число, десятичная запись которого представляет собой бесконечную непериодическую дробь, то эффекта повторяемости уже не будет, т.е. мы будем наблюдать непериодическую (хаотическую) траекторию.
Таким образом, рациональная начальная точка x0 приводит к периодической траектории, иррациональная – к непериодической (хаотической) траектории. Однако проводить вычисления траекторий, выпущенных из иррациональных точек, в аналитическом виде мы не можем. В любом случае при вычислениях нам приходится аппроксимировать иррациональные числа рациональными числами и наблюдать, тем самым, периодические, возможно очень больших периодов, траектории. Поясним последнее. Аппроксимация иррациональных чисел рациональными числами тем точнее, чем больше десятичных знаков в его разложении мы берем. С другой стороны – с увеличением количества знаков увеличивается степень 10n – и в общем случае растет число N, т.е. возрастает период соответствующего цикла.
За последние полвека получен ряд теорем, используя которые можно определить, при каких условиях в дискретных системах возникает сложная нерегулярная динамика (детерминированный хаос). Один из известных результатов носит название теоремы А.Н. Шарковского [6; 7]. Приведем ее в формулировке математиков Т. Ли и Дж. Йорка.
Теорема. Если в дискретной системе имеется цикл периода 3, то имеются циклы любых сколь угодно больших периодов. На рис. 15 изображен один из двух циклов периода 3.
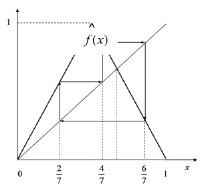
Рис. 15. Цикл периода 3
Каскад бифуркаций и детерминированный хаос
Далее мы кратко рассмотрим пример дискретной системы 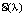 , который уже стал классическим в нелинейной динамике [6]:
, который уже стал классическим в нелинейной динамике [6]:
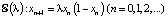 .
.
Здесь 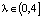 – параметр,
– параметр, 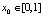 – начальная точка траектории
– начальная точка траектории 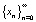 .
.
Можно сказать, что мы будем рассматривать не одну систему, а семейство и следить за динамикой в поведении ее траекторий в зависимости от λ. Оказывается, что траектории в такой системе по мере увеличения параметра λ от 0 до 4 демонстрируют удивительно разнообразное поведение.
Замечание. Квадратичное отображение 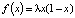 впервые встречается в работах П. Ферхюльста (1845 г.) при описании динамики популяций.
впервые встречается в работах П. Ферхюльста (1845 г.) при описании динамики популяций.
Рассмотрим для начала 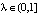 . Тогда
. Тогда 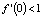 и система имеет единственное устойчивое положение равновесия
и система имеет единственное устойчивое положение равновесия 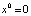 , притягивающее все точки промежутка (рис. 16).
, притягивающее все точки промежутка (рис. 16).
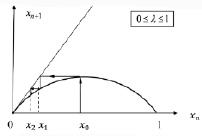
Рис. 16. Траектория стремится к x0 = 0
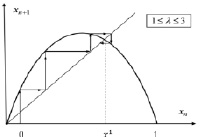
Рис. 17. Траектория стремится к положению
равновесия 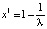
Пусть теперь 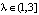 . Тогда x0 = 0 теряет устойчивость, т.к.
. Тогда x0 = 0 теряет устойчивость, т.к. 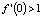 и происходит первая бифуркация: рождается новое положение равновесия
и происходит первая бифуркация: рождается новое положение равновесия 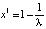 (рис. 17), и оно будет устойчивым до λ = 3, так как при этом
(рис. 17), и оно будет устойчивым до λ = 3, так как при этом 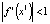 .
.
Пусть 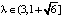 . При λ > 3 происходит следующая бифуркация: положение равновесия x1 теряет устойчивость, и из него рождается цикл периода 2:
. При λ > 3 происходит следующая бифуркация: положение равновесия x1 теряет устойчивость, и из него рождается цикл периода 2: 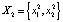 . Здесь
. Здесь 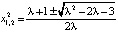 корни уравнения
корни уравнения 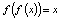 . Числа
. Числа 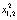 – называются, как уже отмечалось, периодическими точками периода 2 отображения f. Цикл X2 устойчив, так как для его мультипликатора выполняется неравенство
– называются, как уже отмечалось, периодическими точками периода 2 отображения f. Цикл X2 устойчив, так как для его мультипликатора выполняется неравенство 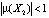 (проверьте это). Поясним геометрически бифуркацию рождения цикла из устойчивого положения равновесия
(проверьте это). Поясним геометрически бифуркацию рождения цикла из устойчивого положения равновесия 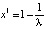 . Для этого изобразим графики отображений f(x) (сплошная линия) и f 2(x) (пунктирная линия) для следующих значений параметра: λ = 2.8 (рис. 18а), λ = 3 (рис. 18b) и λ = 3.2 (рис. 18c). Видно, что при
. Для этого изобразим графики отображений f(x) (сплошная линия) и f 2(x) (пунктирная линия) для следующих значений параметра: λ = 2.8 (рис. 18а), λ = 3 (рис. 18b) и λ = 3.2 (рис. 18c). Видно, что при 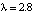
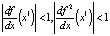 , при λ = 3
, при λ = 3 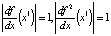 , при
, при 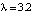
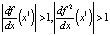 . Таким образом, при λ > 3 уравнение
. Таким образом, при λ > 3 уравнение 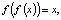 помимо корня
помимо корня 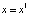 , приобретает два новых корня, которые и образуют цикл
, приобретает два новых корня, которые и образуют цикл 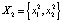 .
.
Рис. 18. Сценарий бифуркации рождения цикла периода 2
Пусть  . При
. При  происходит следующая бифуркация: цикл X2 теряет устойчивость, и из него рождается цикл периода 4:
происходит следующая бифуркация: цикл X2 теряет устойчивость, и из него рождается цикл периода 4: 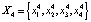 . Здесь
. Здесь 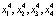 – корни уравнения
– корни уравнения 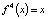 (периодические точки периода 4 отображения f). Цикл устойчив, так как для его мультипликатора
(периодические точки периода 4 отображения f). Цикл устойчив, так как для его мультипликатора 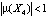 .
.
При λ > 3.54… происходит следующая бифуркация удвоения периода с рождением устойчивого цикла периода 8.
Описанная ситуация происходит до значения 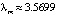 …, при котором притягивающий цикл достигает бесконечно большого периода, а все циклы периодов
…, при котором притягивающий цикл достигает бесконечно большого периода, а все циклы периодов 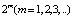 оказываются неустойчивыми. Начиная со значения
оказываются неустойчивыми. Начиная со значения 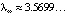 , в системе устанавливается непериодический (случайный) процесс, именуемый детерминированным хаосом. Структурировать предельное множество в этом случае не удается. В таблице приведены бифуркационные значения, при которых рождаются устойчивые циклы периода
, в системе устанавливается непериодический (случайный) процесс, именуемый детерминированным хаосом. Структурировать предельное множество в этом случае не удается. В таблице приведены бифуркационные значения, при которых рождаются устойчивые циклы периода 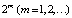 .
.
|
Период цикла |
Значение бифуркационного параметра λm |
|
1 |
|
|
λ1 = 3 |
|
|
2 |
|
|
|
|
|
4 |
|
|
λ3 = 3.544 |
|
|
8 |
|
|
λ4 = 3.56872 |
|
|
16 |
|
|
λ5 = 3.56981 |
|
|
32 |
|
|
λ6 = 3.569934 |
|
|
… |
… |
|
λ∞ = 3.569978 |
|
|
∞ |
Таблица была открыта американским математиком Митчелом Фейгенбаумом – одним из основателей теории детерминированного хаоса. Для полноты приведем ещё один принадлежащий ему результат: для числовой последовательности 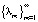 существует предел
существует предел 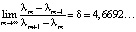 Это число называется сегодня постоянной Фейгенбаума. Причем оказывается, что величина δ для любой дискретной системы, заданной отображением f с единственным максимумом, неизменна, т.е. является инвариантом.
Это число называется сегодня постоянной Фейгенбаума. Причем оказывается, что величина δ для любой дискретной системы, заданной отображением f с единственным максимумом, неизменна, т.е. является инвариантом.
Удивительным в описанной последовательности бифуркаций является не только наличие области в пространстве параметров, с характерным сложным поведением, но и переход от хаоса вновь к порядку, который наступает при значении λ = 3.83. При этом возникают два цикла периода 3: устойчивый и неустойчивый (рис. 19). Видно, что график отображения f3(x) имеет с биссектрисой x семь точек пересечения, абсциссы которых соответствуют устойчивому и неустойчивому циклам и положению равновесия.
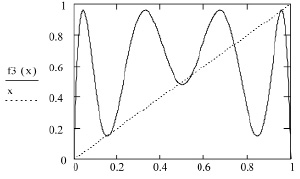
Рис. 19. Абсциссы точек пересечения графика с биссектрисой определяют два цикла (λ = 3.83)
На этом мы здесь остановимся, но обратим внимание, что после значения λ = 3.83 бифуркационная история не заканчивается. О её продолжении можно прочесть в книгах [4; 5; 7].
Замечание. Рассмотренная динамическая система, определяемая квадратичным отображением, несмотря на её внешнюю простоту, оказалась чрезвычайно емким математическим объектом. Ее исследованию в свое время были посвящены десятки научных публикаций, начиная с пионерских работ [6; 7]. О многих теоретических результатах и понятиях мы здесь, естественно, умолчали (эргодичность, перемешивание, корреляционная функция) [3], так как они требуют существенного погружения вглубь теории и выхода за рамки нашей ознакомительной статьи. Однако, несмотря на ограниченность материала, дальнейшее знакомство может быть продолжено в русле программирования и вычислительной математики. В этом направлении можно поставить и провести ряд интересных экспериментальных работ, например в курсе информатики и даже в средней школе.
Критерий детерминированного хаоса
В заключение сформулируем важное определение и один из критериев детерминированного хаоса.
Определение 10. Пусть 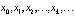 – некоторая траектория динамической системы
– некоторая траектория динамической системы
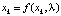 ,
, 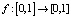 , λ – задано.
, λ – задано.
Число
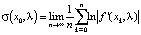
называется её показателем Ляпунова [3; 5].
Показатель Ляпунова характеризует скорость экспоненциального поведения (сближения или разбегания) близких траекторий по отношению к выбранной 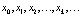 . Доказано, что величина σ(x0, λ) практически не зависит от начальной точки x0 и для больших n становится функцией параметра λ: σ(λ).
. Доказано, что величина σ(x0, λ) практически не зависит от начальной точки x0 и для больших n становится функцией параметра λ: σ(λ).
Критерий: если при заданном значении λ показатель Ляпунова σ(λ) > 0, то система обладает хаотическим поведением траекторий (все траектории экспоненциально разбегаются друг от друга). Если σ(λ) < 0, то – регулярным, т.е. каждая траектория системы при n → +∞ экспоненциально стремится к своему аттрактору (положению равновесия или циклу).
Вычислим, например, показатель Ляпунова для динамической системы, определяемой треугольным отображением. В данном случае он находится тривиально:
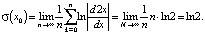
А так как ln2 > 0, то система обладает хаотической динамикой. Спрашивается, есть ли в данной системе циклы? Ответ – есть, но все они неустойчивы, а стало быть, не наблюдаемы в численном эксперименте.
Заключение
В курсе дифференциальных уравнений втузов изучение простых и содержательных эталонных математических моделей должно занять приоритетное место. Такие базовые модели в каждой естественно-научной дисциплине хорошо известны. Этим будет устанавливаться междисциплинарность в обучении, с одной стороны, с другой – подводить к пониманию проблем современной науки, развивать творческую активность и в целом повышать мотивацию студентов к обучению. На этих моделях необходимо демонстрировать методы, приемы и основные результаты. Там, где полный анализ модели осуществить в силу временных рамок невозможно, необходимо теоретический анализ заменить компьютерными экспериментами и тем самым, по возможности, визуализировать результаты [9–11]. Исследование нелинейных моделей при этом должно быть поставлено в центр обучения, ибо нелинейные модели играют и будут играть в дальнейшем в науке центральную роль. Студент по окончании обучения должен четко усвоить, хотя бы на качественном уровне, весь спектр возможного поведения нелинейных систем. Естественно, что обучение надо начинать с простейших динамических систем первого порядка и выработки некоторого понятийного аппарата. Это не потребует большого времени, зато сделает хороший задел для дальнейшего изучения этих вопросов, в том числе и в специальных дисциплинах. В настоящей статье намечен методический подход к изложению основных вопросов первого знакомства с динамическими системами, с опорой на конкретные примеры, набор которых можно с лёгкостью пополнить, воспользовавшись, например, источниками [12–14].


 science-review.ru
science-review.ru