Одной из главных составляющих человеческой жизни во все времена так или иначе являлась математика. Период существования и развития математики как неотъемлемой части системы человеческих знаний в области понятий количества, структуры и соотношения невероятно велик: древнейшие египетские математические тексты относятся ко второму тысячелетию до нашей эры. На протяжении всего своего существования математика развивалась вместе с человечеством, расширяясь вследствие совершенствования собственных методов. Современная трактовка предполагает ее как науку об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств, – именно тех, которые в качестве аксиом положены в основание той или иной математической теории [1].
При этом, являясь наукой абстрактной, формальной, т.е. опирающейся на формальную систему, а не фактическую методологию, математика требует от человека абсолютно уникального мышления. Так, формальная система – это совокупность абстрактных объектов, не связанных с внешним миром, в которой представлены правила оперирования множеством символов в строго синтаксической трактовке без учёта смыслового содержания, то есть семантики. Формальность математики как науки обуславливает необходимость существования определенных методов доказательства истинности или ложности утверждения. Основным инструментом установления истинности или ложности математических утверждений (теорем) является математическое доказательство [2]. Математическое доказательство – это структурированная система логических утверждений, связанных правилами вывода и следующих от аксиом к искомому утверждению.
Целью данной статьи является рассмотрение доказательства методом математической индукции и его практическая реализация в системе компьютерной алгебры Maxima, наиболее оптимальной для данной цели.
Материалы и методы исследования
Главной характеристикой математического доказательства является универсальность, как общеприменимость. Одним из основополагающих универсальных методов математического доказательства является метод математической индукции [3], справедливый для множества натуральных чисел. Суть доказательства утверждений посредством математической индукции состоит из двух этапов:
1. Проверка базы индукции, т.е. проверка истинности утверждения при n = 1.
2. Проверка шага индукции, т.е. проверка истинности утверждения при n = n + 1.
Максимально просто представить данный метод на практике можно через известный всем принцип домино, когда каждая косточка домино опрокидывает следующую, вследствие чего весь ряд из косточек последовательно падает.
Метод математической индукции широко применяется при доказательстве теорем, тождеств, неравенств, при решении задач на делимость, при решении некоторых геометрических и многих других задач. С помощью метода математической индукции можно доказывать различные утверждения, касающиеся делимости натуральных чисел [4, 5].
Распространенность метода математической индукции достаточно широка, и проблема повышения эффективности обучения данному методу обуславливается для современного образования в первую очередь тем, что применение метода математической индукции предполагается в процессе решения некоторых заданий при сдаче Единого государственного экзамена [6]. При этом, анализируя требования актуального на сей день федерального государственного образовательного стандарта общего образования, можно сделать вывод о том, что изучение метода математической индукции включено лишь в программы профильных классов с углубленным изучением математики и имеет достаточно поверхностный характер.
В силу своей одновременной сложности и важности изучение метода математической индукции требует использования в образовательном процессе современных информационных технологий, главными преимуществами которых являются наглядность, удобство использования и значительно более широкие вычислительные возможности, нежели у инструментов традиционного обучения. Также важно заметить, что использование современных образовательных технологий и их программных возможностей в процессе обучения, помимо математической грамотности, способствует развитию компьютерной грамотности обучающегося, повышает его интерес к учебной дисциплине через смену деятельности и актуализирует межпредметную связь с информатикой.
В настоящее время существует достаточно большое количество различных систем и платформ, позволяющих разрешить данную задачу. Среди них можно выделить такие системы, как MathCad, Maple, Mathematica и Maxima. Сравнивая вышеуказанные платформы в рамках разрешения проблемы изучения метода математической индукции в школе, необходимо понимать, что для программы, реализующей символьные вычисления, т.е. преобразования и работу с математическими выражениями в символьной форме [7], метод математической индукции является элементарной задачей. При этом в целях обеспечения успешной интеграции систем компьютерной алгебры в процесс обучения математике в средней школе необходимо обеспечить цифровой копией каждого обучающегося. При существующих сегодня ценах на системы компьютерной алгебры (от 500$ за одну цифровую копию), обеспечение одной образовательной организации полным цифровым пакетом обойдется в сумму около миллиона рублей, что, очевидно, не является целесообразным, учитывая ненадобность большинства из предлагаемых Maple, MathCad или Mathematica функций на ступени среднего общего образования.
Особняком в данном перечне стоит система компьютерной алгебры Maxima, возможности которой также позволяют выполнять символьные вычисления различной сложности, однако распространяется она на бесплатной основе. И очевидно, что наилучшим выбором для решения проблемы совершенствования процесса изучения метода математической индукции в курсе среднего общего образования посредством интеграции в педагогический процесс программных продуктов современных информационных технологий является система компьютерной алгебры Maxima.
Результаты исследования и их обсуждение
Реализация математического доказательства методом математической индукции в системе компьютерной алгебры Maxima требует от пользователя знания таких простейших функций, как:
- sum (выражение, переменная, нижняя граница изменения переменной, верхняя граница изменения переменной), применяющаяся для нахождения суммы n членов ряда, где n принадлежит множеству натуральных чисел [8–10];
- simpsum: true или false как функция активации возможности вычисления бесконечной суммы членов ряда;
- ratsimp (выражение), производящая упрощение и приведение выражения к каноническому виду;
- переменная: значение, как синтаксис присваивания значений переменным;
- mod (x, y) – функция для нахождения остатка от деления;
- if <выражение> then <действие>, как синтаксис условного оператора со значением «если…то…».
Рассмотрим возможную структуру программы для реализации математического доказательства методом математической индукции на различных примерах.
Пример 1. Доказать методом математической индукции следующее равенство: 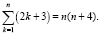
Согласно определению, две части равенства можно считать равными в том случае, если разность левой и правой части выражения равна нулю. Так, первым шагом после записи функции в общем виде необходимо приравнять левую часть выражения к одной переменной (в данной программе – переменной «left»), а правую, соответственно, к другой переменной (в данной программе – «right») (рис. 1).
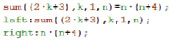
Рис. 1. Приравнивание левой и правой части к соответствующим переменным
Далее, следуя уже определенному выше алгоритму математического доказательства методом математической индукции, необходимо присвоить переменной n значение k и активировать возможность вычисления бесконечной суммы членов ряда, так как на данном шаге будет производиться вычисление такого типа. После чего необходимо создать строку с условной функцией формата «if left-right = 0 then (ok)», и использование возможностей системы компьютерной алгебры Maxima приведет к расчету приведенных функций при n = k и отразит разность между левой части выражения и правой. При разности левой и правой части, равной нулю, Maxima выведет сообщение, приведенное в скобках «(ok)», что будет свидетельствовать об успешном доказательстве равенства при n = k. В случае, если разность левой и правой части нулю не равна, на экране появится выражение «false». Реализация данного этапа приведена на рис. 2.

Рис. 2. Доказательство равенства левой и правой части приведенного выражения при n = k
Следующие два этапа математического доказательства методом математической индукции абсолютно идентичны приведенному алгоритму, с той лишь разницей, что последовательно переменной n присваивается сначала значение n=1 (рис. 3).

Рис. 3. Доказательство равенства левой и правой части приведенного выражения при n = 1, а потом – значение n = k + 1 (рис. 4)

Рис. 4. Доказательство равенства левой и правой части приведенного выражения при n = k + 1
Результатом данной программы будет окно вывода (при условии отсутствия скрытия строки вывода через добавление к строке символа «$»), приведенное на рис. 5.
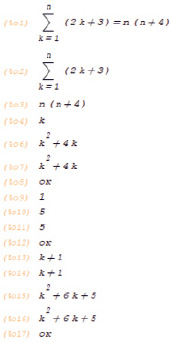
Рис. 5. Окно вывода программы по доказательству приведенного в примере 1 равенства
В целях демонстрации широкого спектра возможностей метода математической индукции, рассмотрим еще один пример, отличный от первого своим заданием.
Пример 2. Доказать, что сумма 5n – 4n + 15 при любом натуральном n делится на 4 (задача заимствована из [11]).
Прежде всего, в целях полного понимания поставленной задачи, уточним формулировку. Так, в примере 2 необходимо доказать, что любое натуральное число, которое возможно представить в виде 5n – 4n + 15, кратно 4.
Решение методом математической индукции с использованием системы компьютерной алгебры Maxima выглядит следующим образом:
Первым шагом вводим данные по условию. Так, обозначим заданное выражение через переменную K и проверим базу индукции (проверим справедливость выражения для n = 1). Для большего удобства введем переменную «itog», присвоив ей значение «mod(K,4)», т.е. переменная «itog» будет равна остатку от деления выражения 5n – 4n + 15, ранее выраженного через переменную K, на 4. Также добавим строку с условной функцией вида «if…then…», задав условие равенства переменной «itog» нулю. При выполнении данного условия, выходная строка Maxima выдаст значение «ок». Проверим справедливость утверждения «остаток от деления выражения 5n – 4n + 15 на 4 при n = 1, равен нулю» (рис. 6).

Рис. 6. Проверка истинности утверждения «остаток от деления выражения 5n – 4n + 15 на 4 при n = 1, равен нулю»
При заданных значениях утверждение является верным, т.к. число 16 делится на 4 без остатка и, соответственно, кратно 4.
Согласно методу математической индукции предположим, что выражение 5n – 4n + 15 делится на 4 при n = k, тогда то же выражение при n = k + 1: 5n+1 – 4n + 11 = K(n) + B, делится на 4, если B делится на 4. Проверим данное утверждение в СКА Maxima, присвоив переменной «LEFT» значение выражения K при n = k, а переменной «RIGHT» значение выражения K при n = k + 1. Так, итогом вычисления «RIGHT-LEFT», т.е. вычисления значения K(n + 1) – K(n), после всех упрощений является 4∙5n – 4, что позволяет сделать заключение о верности утверждения 5n – 4n + 15 при любом натуральном n делится на 4. Результатом решения данного примера в системе компьютерной алгебры Maxima будет окно вывода, приведенное на рис. 7.
Так, приведенные выше решения примеров с различными задачами ярко демонстрируют преимущества использования системы компьютерной алгебры Maxima на уроках математики при изучении доказательства с использованием методом математической индукции.

Рис. 7. Решение примера 2. Окно вывода СКА Maxima
Заключение
Объединяя теоретические умозаключения и практическую реализацию, приведенную выше, можно сделать вывод о том, что использование встроенных функций системы компьютерной алгебры Maxima на уроках математики способствует реализации принципа наглядности и доступности, развитию информационной культуры обучающихся, при этом значительно облегчает усвоение учебного материала. Наличие этих преимуществ, очевидно, демонстрирует положительный эффект интеграции систем компьютерной алгебры в процесс обучения математике, а также актуализирует проблему внесения темы «Метод математической индукции» в базовую программу школьного курса в целях повышения качества обучения математике и развития личной информационной культуры обучающихся.


 science-review.ru
science-review.ru