science-review.ru
«Обучение – это целенаправленный процесс взаимодействия учителя и учащихся, в ходе которого осуществляется образование, воспитание и развитие человека» [1].
Обучение проводится различными способами. Оно зависит от условия проведения, средств, используемых в той или иной деятельности, от среды обучения. Для эффективности процесса обучения учащиеся на уроках должны быть активными. В центре обучения должен располагаться сам ученик, т.е. применяться студентоцентрированный подход к обучению. Поэтому каждый педагог применяет различные методы, приемы и техники обучения, основанные на обновленном содержании.
Некоторые учителя на практике проводят исследовательскую работу и стремятся использовать различные приемы и техники на уроках, исходя из особенностей класса и собственного опыта.
Цель исследования заключается в обобщении опыта по применению авторской техники обучения учащихся на уроках математики, инструкции по его проведению и составлению заданий по уровням сложности.
В педагогической деятельности сталкиваются с разного рода сложностями и решают проблемы за счёт анализа и синтеза тех или иных ситуаций. Математика как предмет является наукой очень серьезной, сложной и требует тщательных знаний, внимательности и сообразительности, поэтому приходится искать пути для активизации процесса обучения через методы, приемы и техники [2].
Авторская техника обучения учащихся, которую применяем на своих уроках математики, называется «Найди, реши и докажи». Эта активная техника применима для средних и старших классов школ. В среднем звене учащиеся воспринимают её очень активно, бурно, а главная цель – победа. В старших классах ученики также активны, но большое внимание уделяют проверке и доказательству задач. У учеников развиваются такие качества, как организованность, сообразительность, внимательность, хорошая память, трудолюбие, решительность, стремление помочь, умение слушать, отстоять свою точку зрения и лидерские качества [3].
Для проведения данной техники понадобится различное количество заданий. Количество заданий зависит от времени выполнения, от того, на каком этапе урока будет проводиться эта активная техника. При подборе заданий немаловажную роль играет выбор разных уровней по одной теме или при закреплении можно использовать несколько тем, а также отдельный раздел.
При подборе заданий можно использовать два варианта распределения по уровням сложности:
1. Дифференцированные задания трех уровней:
A. Базовый уровень, т.е. задания обязательные для всех учащихся.
B. Средний уровень, т.е. задания, усложненные, выполняемые в несколько действий.
C. Продвинутый уровень, т.е. сложные задания, приближенные к олимпиадным задачам [4].
Пример составления дифференцированных заданий по уровням сложности для 10 класса по теме «Производная функции».
Уровень А
Задание 1. Найди производную функции:
а) f(x) = 2x5; b) f(x) = 4 sin x; c) f(x) =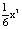 
;
d) f(x) =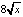 
; e) f(x) = 
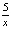; f) f(x) = 7 tg x.
Ответ: а) 10x4; b) 4 cos x; c)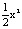 
; d) 4/
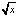; e) – 
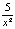; f) 
.
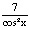Задание 2. Найди производную в точке x0:
a) f´(1), если f(x) =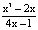 
; b) f´(0), если f(x) = ex sinx;
c) f´(3), если f(x) = 5х²; d) f´(-1), если f(x) = x8 – 3x6 – 7;
е) f´(4), если f(x) =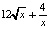 
+ 9.
Ответ: а)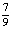 
; b) 1; c) 30; d) 3; e) 2
.
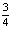Дескриптор обучающийся:
- применяет правила нахождения производной;
- вычисляет производную функции в точке и записывает правильный ответ.
Уровень В
Задание 3. Решить уравнение: f ´(х) = 0
а) f(х) = х³ – 3х² + 7; b) f(х) = (х –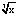 
) 
.
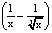Ответ: a) х = 0, х = 2; b) x = 1
Задание 4. Составьте и решите уравнения:
а) f ´(x) = g ´(x), если f(x) = (2x – 1)5 и g(x) = 10x + 7;
b) f ´(x) = – g ´(x), если f(x) = (3x – 5)4 и g(x) = 96x – 17;
c) f ´(x) = – g ´(x), если f(x) = sin²x и g(x) =cos x + cos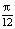 
;
d) f ´(x) = g ´(x), если f(x) = cos²x и g(x) =sin x – sin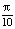 
.
Ответ: а) 0; 1; b) 1; c) πn; ±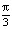 
+ πk; d) 
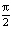+ πn; 
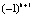
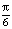+ πk.
Дескриптор обучающийся:
- применяет формулы для нахождения производной;
- применяет правила нахождения производной;
- вычисляет производную функции;
- составляет уравнение;
- решает уравнение;
- записывает правильный ответ.
Уровень С
Задание 5. Составьте и решите неравенство:
а) f ´(x) ≤ f ´´(x), если f(x) =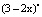 
;
b) f ´(x) ≥ f ´´(x), если f(x) =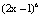 
Ответ: а) (- ∞; 4,5]; b)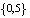 
U[5,5; +∞).
Задание 6. Найдите производную сложных функций:
а) f(x) =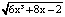 
; b) f(x) = 2cos23x; c) f(x) = 56–2x + 15;
d) f(x) = log4 (1 – 6x) + 3; e) f(x) = 2 ln(5 – 2x).
Ответ: а)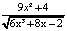 
; b) -6sin6x; c) 
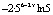; d) 
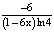; e)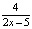 
.
Дескриптор обучающийся:
- применяет формулы для нахождения производной;
- применяет правила нахождения производной;
- вычисляет производную функции;
- составляет неравенство;
- решает неравенство и записывает правильный ответ.
Дополнительное задание
Докажите, что при всех допустимых значениях х верно равенство
а) для f(x) =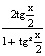 
и g(x) = 
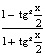, f ´(x)· g´(x) = – f(x)·g(x); b) для f(x) =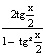 
и g(x) =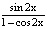 
, 
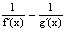= 1; c) для f(x) =1 + 
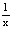, ( f(f(x)))´ = – 
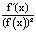[5].
2. Задания, построенные по таксономии Блума:
Знания – определения, факты, терминология конкретного материала.
Понимание – объяснение, интерпретация, экстраполяция.
Применение знаний в различных ситуациях.
Анализ – взаимосвязи элементов и принципы построения.
Синтез – план и система действий, основанная на знаниях из различных областей, экспериментирование, получение системы абстрактных отношений.
Оценка – суждение на основе имеющих данных, внешних критерий [6].
Показан пример составления задания по таксономии Блума для 8 класса по теме «Решение квадратных неравенств».
Уровень – Знания
Задание 1. Выбери из данных неравенств квадратные:
а) х² +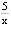 
– 12 < 0; b) -х² + 7х + 1 ≤ 0; c) -m² + 3m + 5 > 0;
d) 5х² + 8y + 6 ≤ 0; e)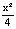 
+ 7х ≥ 0; f) -5х² + 9х ≤ 21.
Дескриптор:
- определяет квадратное уравнение.
Ответ: b, c, е, f.
Задание 2. На рис. 1 изображен график функции f(x) = -5х² + 3х + 2.
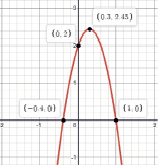
Рис. 1. График функции
Используя график функции, определи решение неравенств:
a) -5х² + 3х + 2 ≥ 0 b) -5х² + 3х + 2 ≤ 0
c) -5х² + 3х + 2 > 0 d) -5х² + 3х + 2 < 0
Дескриптор:
- определяет точки пересечения графика с осью ох;
- находит промежутки, удовлетворяющие условию (а);
- находит промежутки, удовлетворяющие условию (b);
- находит промежутки, удовлетворяющие условию (c);
- находит промежутки, удовлетворяющие условию (d);
Ответ: a) [-0,4; 1]; b) (-∞; -0,4]U[1; + ∞); c) (-0,4; 1); d) (-∞; -0,4)U(1; + ∞).
Задание 3. Реши квадратные неравенства:
а) х² – 16 < 0; b) -у² + 3у ≤ 0; c) 4m² + m – 5 > 0; d) 5n² ≤ 0.
Дескриптор:
- находит нули квадратичной функции;
- определяет схематическое расположение параболы относительно оси абсцисс;
- находит промежуток соответствующий неравенству.
Ответ: а) (-4; 4); b) (-∞; 0]U[3; + ∞); c) (-∞; -1,25)U(1;+∞); d) {0}.
Уровень – Понимание
Задание 4. Найди целые решения квадратных неравенств:
а) 4х² + 4х ≥ -1; b) 2n² + 4n + 3 ≤ 0; c) -3m² + 2m + 5 ≥ 0; d) 25у² + 9 ≤ 30y.
Дескриптор:
- решает квадратное уравнение;
- находит числовой промежуток;
- определяет число целых решений неравенства.
Ответ: а) х ϵ Z; b) х ϵ Ø; c) х ϵ {-1; 0; 1}; d) х ϵ {0,6}.
Задание 5. Реши квадратные неравенства методом интервалов:
а) 3х² – 7х ≥ 0; b) 0,5n² + 3n + 2,5 ≤ 0; c) -2m² + 9m > 4; d) -3у² + 6y – 5 < 0.
Дескриптор:
- решает квадратное уравнение;
- находит числовой промежутки;
- определяет число целых решений неравенства.
Ответ: а) (-∞; 0)U(2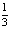
; +∞); b) [-5; -1]; c) (0,5; 4); d) (-∞; + ∞).
Задание 6. На рис. 2 изображены графики квадратичной функции y = ax2 + bx + c. Определите при каких значениях х значения у будут:
a) положительные; b) отрицательные;
с) не положительные; d) не отрицательные.
1) 2) 3)
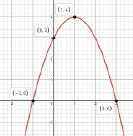
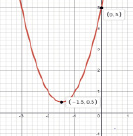
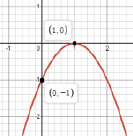
Рис. 2. Графики квадратичной функции
Дескриптор:
- определяет точки пересечения графика с осью ох;
- находит промежутки удовлетворяющее условию (а), (b), (c), (d)
Ответ:
1) a) (-1; 3); b) (-∞; -1)U(3; + ∞); c) (-∞; -1]U[3; + ∞); d) [-1; 3].
2) a) (-∞; + ∞); b) Ø; c) Ø; d) (-∞; + ∞).
3) a) Ø; b) (-∞; 1)U(1; + ∞); c) (-∞; + ∞); d) 1.
Уровень – Применение
Задание 7. Найди наибольшее значение неравенства и получи факты о животных:
a) гепард бежит со скоростью -0,1х² + 10х + 110 ≥ 0 км/ч;
b) у кенгуру рекордный прыжок в высоту составил -5х² + 11х + 16 ≥ 0 м;
с) верблюды могут не пить воду около 0,2х² – 4х – 60 ≤ 0 дней.
Дескриптор:
- выбирает способ решения полученного неравенства;
- находит решение неравенства;
- записывает ответ в соответствии с условием задачи.
Ответ: a) 110 км/ч; b) 3,2 м; c) 30 дней.
Задание 8. Найди область определения функции:
a) у =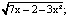 
b) у = 
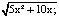c) у = 4 –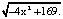 
Дескриптор:
- определяет одз для подкоренного выражения;
- составляет квадратное неравенство;
- решает квадратное неравенство;
- находит область определения функции.
Ответ: a) [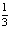
; 2]; b) (-∞; -2]U[0; + ∞); c) (-6,5; + 6,5).
Задание 9.
a) ширина прямоугольника на 5 см больше его длины. Какой должна быть длина прямоугольника, чтобы его площадь была не меньше 36 см2?
b) уравнение h = -4t² + 12t + 2 описывает высоту h (м) мяча в каждый момент времени t(сек), (t ≥ 0). Сколько секунд будет мяч на высоте выше 10 м?
с) когда в бейсбольный мяч бьют битой, то высота мяча в момент времени t(сек), (t ≥ 0) достигает h (м), а ее траектория выражается функцией h = -12t² + 16t + 9. В какой промежуток времени высота мяча будет выше 13 м?
Дескриптор:
- составляет неравенство по условию задачи;
- выбирает способ решения полученного неравенства;
- находит решение неравенства;
- записывает ответ в соответствии с условием задачи.
Ответ: a) [4; + ∞); b) (1; 2); c) (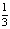
; 1).
Уровень – Анализ
Задание 10. Реши квадратные неравенства:
а) 11 – (х + 1)² ≥ 0; b) (2у – 8)² – 4у(2у – 8) ≥ 0;
c)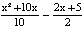 
≤ 0; d) х > 
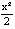– 4х + 5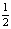
Дескриптор:
- преобразовывает неравенство;
- решает полученное неравенство;
- записывает правильный ответ.
Ответ: а) [-5; 2]; b) [-4; 4]; c) [-15; 15]; d) (5 –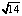 
; 5 + 
).
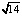Задание 11. Найди область определения функции:
a) у =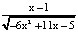 
; b) у = 
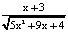; с) у =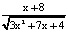 
Дескриптор:
- использует свойства корня и дроби;
- составляет квадратное неравенство;
- решает неравенство;
- записывает область определения функции.
Ответ: a) (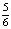
; 1); b) (
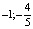); c) (
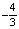; -1).
Уровень – Синтез
Задание 12.
a) При каких значениях m неравенство -x² – (m – 2)x – 1,5m + 3 < 0 имеет решение?
b) При каких значениях х график функции у = x² – 14x + 49 имеет не положительные значения?
с) При каких значениях m неравенство x² + 6x + 5m² – 6m + 1 > 0 имеет два корня?
Дескриптор:
- находит дискриминант относительно переменной х;
- находит дискриминант относительно переменной m;
- решает неравенство d ≥ 0;
- записывает промежуток для переменной m.
Ответ: a) [2; 8]; b) 7; c) (-4; 10).
Задание 13.
a) Произведение четного натурального числа и его половины больше 17, но меньше 25. Найди эти числа.
b) Если к квадрату натурального числа, увеличенного на единицу, прибавить 1, то полученная сумма будет больше 10. Если прибавить 5, то полученная сумма будет меньше 30. Найди натуральное число.
с) Если квадрат натурального числа, уменьшенного на единицу, увеличить на 4, то полученная сумма будет меньше 20. Найди натуральное число.
Дескриптор
- составляет по условию задачи неравенство;
- решает неравенство;
- находит правильное решение.
Ответ: a) 6; b) 4; c) 1 и 2.
Задание 14.
а) Длина прямоугольника больше 45 см, а ширина составляет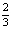 
его длины. Верно ли, что площадь прямоугольника больше 900 см²?
в) Одна сторона прямоугольника больше другой на 4 дм. Какими могут быть стороны прямоугольника, если его площадь меньше 15 дм2?
Дескриптор:
- составляет неравенство в соответствии с условием задачи;
- решает неравенство;
- оценивает неизвестный элемент;
- записывает правильный ответ.
Ответ: a) верно; b) ширина 0 < х < 3, длина 4 < х < 5.
Задание 15. При каких значениях а все точки графика функции:
a) у = х² – 4ах + а(а – 1) расположены выше оси Ох;
b) у = -х² + 6ах + а(а + 1) расположены ниже оси Ох;
с) у = ах² + 2(а + 1)х + 4а расположены не ниже оси Ох.
Дескриптор:
- составляет неравенство по условию задачи;
- решает неравенство;
- оценивает неизвестный элемент;
- записывает правильный ответ.
Ответ: а) а ϵ (-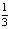
; 0); b) а ϵ (-0,1; 0); с) а ϵ [1; +∞), при а > 0 [7, 8].
Задания, сформированные в карточках, желательно разграничить по уровням в зависимости от цвета. Допустим, задания от простого к сложному при дифференцировании распределим следующим образом: зеленый, желтый, красный. При оформлении заданий, построенных по таксономии Блума, можно использовать цвета от бледного к более яркому.
После составления заданий, как и во всех методах, приемах и техниках, необходимо сформулировать четкие правила поведения учеников и учителя для выполнений заданий. Так как при проведении техники «Найди, реши и докажи» имеется большое количество заданий, нужны четкие установки для их выполнения.
Правила для учеников:
1. Быть вежливым, уважать друг друга.
2. Уметь выслушать, не перебивать.
3. Довести свою точку зрения до слушателей, признавать свою ошибку.
4. Работа индивидуальная, переходящая в дискуссию.
5. Выбрав любые понравившиеся задания, решить их предельно правильно и грамотно так, чтобы смог доказать свое решение.
6. Решай, проверяй, доказывай, побеждай.
Правила для учителя:
1. Выдает задания.
2. Следит за дисциплиной.
3. Является наблюдателем.
4. Не отвечает на вопрос: «Кто прав?»
5. Корректирует вопросы и ответы учеников.
Для проведения техники также необходимо приготовить площадку для ответов учащихся и фишки для накопления бонусов. На школьной доске либо на интерактивной доске заранее заготавливаются номера всех заданий. Первый ученик, выполнивший задание, записывает правильный ответ напротив данного задания и берет одну фишку. Остальные ученики, как только выполнят задание, проверяют его на правильность. Если задание верно, то фишка остается у первого ученика, но если же ответ не сходится с ответом другого ученика, то ученики выходят на бой. Каждый ученик должен расписать свое решение и доказать свою правоту, вступая в дебаты. Если первый ученик доказал свое решение, то второй терпит поражение и фишка остается у первого ученика. Если же второй доказывает правоту своего решения, то он забирает у первого ученика его фишку. Так продолжается решение всех заданий, в конце подводится итог по количеству фишек у учеников.
Заключение
Из практического опыта делаем вывод, что не все ученики справляются с некоторыми заданиями, так как не понятны решения той или иной задачи. Поэтому подводя итог данного соревнования, необходимо уточнить, какие возникли вопросы при решении и кому необходимо объяснить то или иное задание. Ученики-лидеры объясняют решение сложных заданий, с которыми не справились учащиеся, т.е. оказывается менторская помощь.
Исследование показало, что данная техника направлена на развитие у ученика следующих качеств: самообразование, воспитание, активность, критическое, рефлексивное мышление и лидерские качества. Отличительной стороной данной техники является как групповая, так и индивидуальная работа. В результате применения такой активной техники успеваемость и качество знаний учащихся имеет положительную динамику.