Scientific journal

Научное обозрение. Педагогические науки

ISSN 2500-3402

ПИ №ФС77-57475

В процессе профессионального становления военных специалистов важную роль играет формирование таких качеств, как визуально-тактильное восприятие протекающих процессов, пространственное и абстрактное мышление. Достичь этого возможно на занятиях по физике, выполняя поисковые, частично поисковые задания. Формами таких заданий являются лабораторные работы, расчетно-графические работы, кейс-задания, а также военно-научная работа курсантов. В последнее время актуализировалось использование в образовательном процессе кейс-заданий [1–3]. Это связано с тем, что данные дидактические материалы органично соединяют учебную и научно-исследовательскую деятельности. Предполагается, что это, с одной стороны, позволит улучшить методическое обеспечение и укажет направления модернизации материально-технической базы, а с другой стороны, улучшит понимание и усвояемость у обучающихся наиболее сложных и важных разделов изучаемого материала дисциплины. Поэтому данная работа посвящена разработке кейс-заданий на примере лабораторной работы «Определение главных моментов инерции модели самолета».

Цель исследования состояла в разработке методики составления кейс-задания, критериев оценки эффективности принятого решения, выборе существующих способов решения творческих заданий, методов оценки эффективности принятия решения.

Материалы и методы исследования

Для реализации поставленной цели проведен анализ научной литературы, дидактического материала, нормативных документов. Тема кейс-задания связана с необходимостью модернизировать установку для выполнения лабораторной работы «Определение главных моментов инерции модели самолета», а также усовершенствования ее методики выполнения. Рассмотрены следующие проблемы, решение которых необходимо представить в рамках кейс-задания:

1. Уменьшение погрешности измерений. Это связано с толщиной нити и длиной шкива, так как для уменьшения трения и запутывания нити во время падения груза, её необходимо наматывать на шкив в один слой, что уменьшает возможный пройденный путь грузом при падении и время падения.

2. Уменьшение погрешности определения главных моментов модели самолета. График зависимости углового ускорения ԑ от разгоняющего момента силы М строится по трем точкам, что явно недостаточно и может приводить к существенной погрешности определения момента силы трения и главных моментов модели самолета.

3. Влияние использования на точность вычисления главных моментов инерции модели самолета по осям Оz и Оy момента трения, найденного относительно оси Ох.

4. Техническое решение по замене электрического секундомера 1957 г. выпуска, используемого в работе, на более современное устройство.

5. Верификация полученных данных.

6. Выявление иной проблемы методологического или технического характера и её возможное решение.

При выполнении лабораторной работы «Определение главных моментов инерции модели самолета» [4] используются следующие приборы и принадлежности: установка для определения моментов инерции модели самолета, электрический секундомер, набор грузов (100 г, 200 г, 300 г).

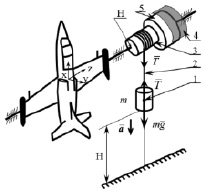
Схема лабораторной установки

Лабораторная установка состоит из рамы, на которой установлены подвижный и неподвижный подшипники для закрепления модели в трёх различных положениях. Модель самолёта соединяется соосно с валом, на котором закреплены два шкива 3 и 5 (рисунок). Один из них (5) используется для торможения электрическим тормозом (4), а другой (3) служит для создания вращения модели с помощью груза, подвешенного на нити 2, намотанной на шкив 3. Ниже рамы установлена масштабная рейка, по которой перемещается площадка с концевым выключателем электрического тормоза. При попадании груза на площадку электрический секундомер выключается, а тормоз включается автоматически.

Для приведения во вращение модели самолёта к свободному концу нити 2 (рисунок), намотанной на шкив, прикрепляется груз 1 (рисунок) массой m. При падении груза нить натягивается с силой Т и создаёт вращающий момент: M = T∙R, где R – радиус шкива.

Ускорение, с которым движется груз, и угловое ускорение вращения шкива взаимосвязаны:

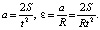
На основании 2-го закона Ньютона можно записать

ma = mg – T => T = m∙(g – a).

Тогда выражение момента силы примет вид

M = m∙(g – a)∙R.

На вращающуюся систему кроме разгоняющего момента сил Μ действует определённый момент сил трения Mтр., который необходимо вычислить, используя график зависимости углового ускорения ԑ от разгоняющего момента силы М. Момент инерции для выбранной оси самолёта рассчитывается по формуле

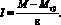
А относительную погрешность определения момента инерции можно вычислить по упрощённой формуле

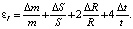
Для решения указанных выше проблем выбран один из наиболее эффективных и интересных системных методов решения творческих технических задач – морфологический анализ [5, 6], состоящий в выявлении нескольких морфологических признаков (важных параметров) и составлении всех возможных их сочетаний.

В процессе использования данного метода придерживались следующего алгоритма:

1. Сформулировали проблему, подлежащую решению, цель задачи, которая состоит в поиске новых вариантов схем, методик, принципов действия, конструктивных решений разрабатываемой системы. При этом исследование можно проводить одновременно по нескольким признакам.

2. На следующем шаге необходимо исследуемую систему разбить на несколько основных частей (узлов) и выявить параметры, которые подлежат модификации. Рекомендуется выбирать при ручной обработке число узлов от 4 до 7. Удобно решать задачу, применяя морфологический метод несколько раз: сначала для наиболее важных узлов, а затем для дополнительных, второстепенных или выявленных в ходе анализа новых узлов и представляющих интерес.

3. Далее необходимо создать многомерную матрицу (морфологический ящик), содержащую возможные решения проблемы.

4. После этого анализируются решения, сформированные в морфологическом ящике, и оценивается их эффективность.

5. На заключительном этапе выбираются и реализуются наилучшие решения.

Для наглядности применения описанного метода решения творческих задач приведем пример модификации стула. Для этого выделяем важные узлы, которыми могут быть ножки стула, сиденье, спинка. Далее формируем морфологический ящик (табл. 1).

Возможные сочетания решений рассматриваемой проблемы имеют вид (А1; Б1; В3), (А3; Б1; В3) и т.д. Число возможных сочетаний в морфологическом ящике находится как произведение количества элементов в строках: 4*5*5 = 100.

В приведенном примере каждый узел имеет решение по одному свойству. Например, ножки – по их числу, сиденье – по форме, спинка стула – по форме и пространственной ориентации. Однако можно модифицировать каждый узел по нескольким параметрам, но в этом случае увеличивается число возможных решений и обработка данных вручную становится затруднительной. Кроме того, выбор оптимального решения тоже требует больших затрат времени и автоматизированного анализа. Но при указанных затруднениях появляется большая вариативность решения, что позволяет выбрать наиболее продуктивное решение.

В процессе оценки эффективности решений творческих заданий можно использовать большое количество методов используемых в педагогике, социологии, метрологии, теории принятия управленческих решений, экономике. В данной работе предлагается два варианта оценки эффективности принятого решения: метод ранжирования и метод экспертных оценок.

Если оценку эффективности осуществляет один человек – преподаватель или эксперт, выбранный из числа обучаемых, то используется метод ранжирования, в противном случае выбираются несколько экспертов из числа обучаемых, которые выполняют эту работу в рамках метода экспертных оценок.

Критериями оценки эффективности решения выберем такие показатели, как себестоимость, доступность, времязатраты, оригинальность.

Рассмотрим более детально каждый из вариантов. Метод ранжирования состоит в расположении оцениваемых объектов в определенной последовательности (убывания или возрастания показателей) и определении их места в этом ряду. В процессе использования данного метода составляется таблица, в которую вносятся полученные творческие решения и принятые критерии оценки. Затем каждому решению по указанным критериям присваивается ранг (индекс) от 1 до 3. Первый ранг, например, имеет неудовлетворительное решение, третий ранг – наиболее удачное. Ранжировать можно и наоборот: худшему решению присваивать наибольший ранг, наилучшему – наименьший. Если решения имеют одинаковую значимость, по мнению эксперта, то в этом случае обоим присваивается одинаковый ранг.

Затем по каждому решению находится суммарный ранг и по его значению отбираются решения с наибольшим или равными (связанными) рангами. Затем процедура повторяется с выбранными решениями, остальные более не рассматриваются. Рассмотрим описанную процедуру на примере модификации модели стула, описанного выше (табл. 2).

В случае оценки эффективности решений экспертами ранжирование решений производится аналогично [7]. Затем проверяется согласованность действий экспертов, которая определяется с помощью коэффициента конкордации Кендалла:

,

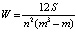где S – сумма квадратов отклонений всех оценок рангов каждого критерия эффективности экспертизы от среднего значения; n – число экспертов; m – число критериев эффективности экспертизы.

Коэффициент конкордации изменяется в диапазоне 0 < W < 1, причем 0 – полная несогласованность мнений, 1 – полное единодушие экспертов.

Рассмотрим экспертный метод ранжирования на примере модификации стула. Для оценки эффективности решения выбрано четыре эксперта, которые по данному решению ранжировали критерии эффективности. Определим согласованность мнений экспертов по данным вышеприведенного примера. Расчеты представим в табл. 3.

Рассчитаем коэффициент конкордации:

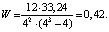
Полученный коэффициент конкордации имеет допустимое значение согласованности мнения экспертов, что позволяет продолжить решение задачи. Расчет коэффициента конкордации Кендалла удобнее производить с помощью редакторов персонального компьютера, например, Excel.

Заключение

Таким образом, выполненная работа позволила разработать методику составления кейс-задания на примере лабораторной работы «Определение главных моментов инерции модели самолета», критерии оценки эффективности принятого решения, выбрать методы оценки эффективности принятия решения из существующих способов решения творческих заданий. Данное исследование позволит составлять кейс-задания по другим темам, изучаемым в рамках дисциплины «Физика» высшего военного профессионального образования, а также выполнять военно-научную работу с курсантами. Разработанная методика составления кейс-заданий позволит уменьшить времязатраты на составление подобных заданий, осуществить модернизацию методики выполнения, материальных и технических средств, используемых при выполнении лабораторных и научно-исследовательских работ, а также повысит усвояемость и понимание у обучающихся наиболее сложных разделов изучаемого предмета.