Математика является одной из основополагающих наук, в которой изучаются не только числа, но и множество других немаловажных разделов. В данной статье речь пойдет о математических доказательствах. Если рассматриваемое утверждение логически следует из уже доказанных и обоснованных утверждений, то оно является истинным [1].
Таким образом, дедуктивный метод считается основой математического доказа- тельства.
Из вышесказанного следует, что математическое доказательство – это своего рода рассуждение с целью дальнейшего обоснования истинности какого-либо утверждения. Одним из универсальных методов доказательства является метод математической индукции.
Применение знаний и навыков использования данного метода предполагается при решении множества задач. Выпускники средних общеобразовательных организаций при сдаче Единого государственного экзамена (ЕГЭ) сталкиваются с заданием, которое, в свою очередь, предусматривает применение метода математической индукции.
Проведя анализ требований Федеральных государственных образовательных стандартов (ФГОС), заметим, что, несмотря на вышеизложенные факты, изучение метода математической индукции (ММИ) включено лишь в программы профильных классов с углубленным изучением математики. Но даже на этом уровне с ММИ учащихся знакомят только поверхностно [2, 3].
Цель исследования: ответить на вопрос: «Как следует строить процесс обучения математике, а конкретно решение задач с использованием методом математической индукции с использованием системы компьютерной алгебры Maple?»
Материалы и методы исследования
Метод математической индукции – один из основополагающих способов доказательства утверждений, справедливых на множестве натуральных чисел (иногда утверждения могут быть сформулированы для всех натуральных чисел, иногда – на множестве натуральных четных чисел и т.п.) [4].
Основой доказательства утверждений с помощью ММИ является:
Утверждение P(n) (где n – натуральное число), которое справедливо при n ∈ N, если:
1. База индукции (базис индукции). На данном этапе проверяется истинность утверждения, как правило, при n = 1. Таким образом, утверждение P(n) справедливо при n = 1.
2. Индуктивный переход (шаг индукции). Считая, что утверждение P(k) справедливо при n = k, соответственно проверяется истинность утверждения P(k + 1) при n = k + 1[3, 5].
Метод математической индукции зачастую применяется при доказательстве:
1) делимости и кратности;
2) равенств и неравенств;
3) тождеств;
4) последовательности и суммы [4, 6].
Результаты исследования и их обсуждение
При рассмотрении образовательного процесса в условиях реализации современных информационных технологий очевидным становится то, что для наилучшего усвоения знаний учащихся осуществляется продуктивное внедрение современных средств обучения, которые, в свою очередь, помогают активизировать мыслительную деятельность учащихся, способствуют развитию творческой деятельности всех участников образования. А также, что немаловажно и актуально на сегодняшний день, позволяют проводить занятия дистанционно и активно влиять на повышение эффективности образовательного процесса. Перечисленные вопросы являются одной из важнейших проблем сегодняшнего дня [7, 8].
Кроме того, при применении на уроках математики информационных технологий осуществляется взаимосвязь с информатикой, что позволяет говорить о межпредметных связях в развитии методики обучения, общеобразовательной школы и способствует модернизации учебно-воспитательного процесса.
Одной из возможностей решения вышеизложенных вопросов является применение системы компьютерной алгебры (СКА) Maple в ходе изучения ММИ.
CKA Maple представляет собой программный пакет, содержащий более двух тысяч команд, которые позволяют производить аналитические вычисления на компьютере, такие как решение задач алгебры, геометрии, математического анализа, дифференциальных уравнений, статистики, математической физики и т.д. [9, 10].
Решение математических задач с использованием СКА Maple, в свою очередь, позволяет учащимся осуществить доказательство методом математической индукции, произвести экономию время при проведении урока, способствует инновационному и наглядному изучению различных тем школьного курса.
СКА Maple предусматривает встроенное наличие функции simplify, которая позволяет производить упрощение символьных выражений, формат этой команды позволяет указать в качестве параметров для преобразования практически любое выражение. Если упрощение произвести невозможно, функция возвращает исходное выражение [11].
Для задания (вычисления) суммы в СКА Maple используется встроенная функция sum, для вычисления значения факториала команда factorial, а для введения значения пределов изменения суммы до бесконечности – infinity [12].
Примеры доказательства делимости и кратности
Пример 1. Доказать, что сумма 5n – 4∙n + + 15 при любом натуральном п делится на 4 (задача заимствована из [13]).
Эта задача может быть сформулирована более точно: «Доказать, что все натуральные числа, которые можно представить в виде 5n – 4∙n + 15, делятся на 4».
Решение:
Решение методом математической индукции.
Выразим заданную сумму (обозначим заданное выражение) через переменную K;
> restart;
> K: = n->5^n-4*n+15;
K≔n → 5n – 4∙n + 5
Изначально проверяется справедливость утверждения для K(1):
> K(1);
16
При заданных значениях утверждение является верным, так как число 16 кратно 4.
Предположим, что утверждение K справедливо при n = 1, k ≥ 1, то есть число 5n – 4∙n + 15 – делится на 4, тогда число K(n + 1) = 5n+1 – 4∙n + 11 = K(n) + B делится на 4, если B делится на 4. Проверим данное утверждение:
> B:=K(n+1)-K(n);
B≔5(n+1) – 4 – 5n.
Для упрощения полученного выражения воспользуемся встроенной функцией simplify ( % означает выполнение операции с предыдущим значением) [4].
> simplify(B);
4∙5n – 4.
Полученное выражение можно представить в виде произведения:
> evalb(4*5^n-4=4*(5^n-1));
true
Что позволяет утверждать, выражение вида 5n – 4∙n + 15 – делится на 4, так как 5n – 1 делится на 4 при любых n ≥ 0, а значит, произведение делится на 16.
Вывод: Данное утверждение верно. Задача решена.
Пример 2. Доказать, что сумма n3 + + 6∙n2 + 29n кратна 6.
Решение:
Для доказательства истинности данного утверждения воспользуемся методом математической индукции.
Выразим заданную сумму (обозначим заданное выражение) через переменную P;
>P:=n->n^3+6*n^2+29*n;
P∶ = n –> n3 + 6n2 + 29n.
Таким образом получим решение функции P при n равном 1;
>P(1);
36.
Далее следует выразить значение разности функций P от n + 1 и n;
>P(n+1)-P(n);
(n + 1)3 + 6(n + 1)2 + 29 – n3 – 6n2.
Применим ранее рассмотренную функцию simplify ( %), для упрощения, полученного выражения, где % означает выполнение операции с предыдущим значением [4].
>simplify( %);
3n2 + 15n + 36.
В вышеприведенном значении кратность 6 не очевидна, для более наглядного представления найдем полную индукцию, то есть применим метод математической индукции повторно.
Полученную функцию 3∙n2 + 15∙n + 36 зададим через новую переменную W;
>W:=n->3*n^2+15*n+36;
W∶ = n –> 3n2 + 15n + 36.
Проверим справедливость утверждения: значение функции W при n равном 1 должно быть кратно 6:
>W(1);
54.
Утверждение доказано и является верным.
Найдем значение разности функций от n + 1 и n;
>W(n+1)-W(n);
3(n + 1)2 + 15 – 3n2.
Упростим полученное выражение;
>simplify ( %);
6n + 18.
Проверим выполнение условия выражения, кратность 6, путем деления предыдущего выражения на 6;
> %/6;
n + 3.
Вывод: Очевидным становится то, что условия метода математической индукции выполнены, следовательно, выражение является истинным, что и требовалось доказать.
Пример доказательства равенств
Пример 3. Доказать равенство 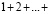
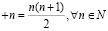 [14].
[14].
Решение:
Зададим сумму из данного равенства:
>restart; sum(i, i=1…n);
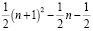 .
.
Произведем упрощение полученного выражения для суммы:
>H:= simplify ( %);
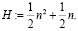
Выполним сравнение левой и правой части равенства:
>simplify (n*(n+1)/2-H);
0.
Вывод: Предположение равенства суммы является верным. Для доказательства данного равенства использовалась функция simplify.
Пример 4. Доказать равенство

Решение:
Для доказательства данного равенства с помощью СКА Maple разделим его на левую и правую части, которые зададим переменными L и R соответственно.
Зададим левую часть равенства через переменную L, выразив ее суммой
>L := sum(n/factorial(n+1), n = 1 .. infinity);
L := 1.
Аналогичные действия выполняются для правой части равенства;
>R: = sum(1/(n*(n+1)), n = 1 .. infinity);
R := 1.
Применим метод математической индукции, для доказательства истинности данного утверждения, получим значение при n равном 1(база индукции);
>L(1);
1.
>R(1);
1.
Соответственно, выразим обе части равенства последовательно, при значении n + 1 (Индуктивный переход);
>L(n+1);
1.
>R(n+1);
1.
Далее выразим значение разности от n + 1 и n, задав через новые переменные L1 и R1;
>L1 := L(n+1)-L(n);
L1 := 0.
>R1 := R(n+1)-R(n);
R1 := 0.
Покажем равенство;
>L1 = R1;
0 = 0.
Вывод: Метод математической индукции выполнен, следовательно, выражение истинно, что и требовалось доказать.
Пример доказательства неравенств
Пример 5. Доказать, что при n∈N, n ≥ 5 справедливо неравенство 2n ≥ n2 + n + 2.
Решение:
Проверим верность утверждения при n = 5:
> evalb(2^5>=5^2+5+2);
true
Допустим справедливость утверждения при п = k ≥ 5
> 2^k> = k^2+k+2;
k2 + k + 2 ≤ 2k.
Вышеприведённое выражение равносильно следующему выражению:
> 2^k-k^2-k-2> = 0;
0 ≤ 2k – k2 – k – 2.
Докажем справедливость неравенства при n = k + l
> 2^(k+1)-((k+1)^2-(k+1)-2);
2(k+1) – (k + 1)2 + k + 3;
> simplify( %);
2(k+1) – k2 – k + 2.
Вывод: Данное выражение больше нуля при k ≥ 5. Таким образом, задача решена.
Очевидно, что применение встроенных функций СКА Maple позволяет осуществить возможность наглядного и доступного доказательства различных тождеств с использованием ММИ, что значительно облегчает работу педагога, и, таким образом, решение различных задач школьного курса математики методом математической индукции способствует более облегченному усвоению тем.
Выделим преимущества применения в ходе учебного процесса СКА Maple, такие как: возможность избежать арифметических ошибок, значительное сокращение времени проведения урока, кроме того, появляется уникальная возможность более точного планирования рабочих программ. Представленные инновационные подходы могут явиться основанием для внесения темы «Метод математической индукции» в базовую программу школьного курса, что в свою очередь позволяет говорить о более полном овладении знаниями по данной теме учащимися выпускных классов [15].
Заключение
Изучение метода математической индукции с применением СКА Maple может существенно повлиять на развитие общеобразовательных знаний и расширение кругозора обучающихся, способствовать более детальной подготовке школьников к единому государственному экзамену. Кроме того, текущие обстоятельства (ведение занятий дистанционно) диктуют необходимость наличия и использования универсальных и интерактивных программ обучения.
Педагогическая деятельность в условиях современной информационной образовательной среды становится значительно доступнее, появляется возможность облегчить работу педагога и позволяет ему более доступно представить материал.


 science-review.ru
science-review.ru