science-review.ru
Правильная геометрическая подготовка будущих учителей математики имеет большое значение в формировании их универсальной и профессиональной компетентностей, кроме того, является предпосылкой для развития геометрических знаний и мышления учащихся общеобразовательной школы. Эффективность преподавания геометрии в общеобразовательной школе и в вузе зависит от многих факторов, одним из которых является наглядность. Наглядность «способствует реализации основного принципа доступности, а также успешности формирования понятий, методов, приёмов, поддержанию интереса к математике, приводит к более высокому уровню развития математической культуры, математического языка, логического мышления, обоснованности суждений» [1].
Основоположником принципа наглядности, применяемого в обучении, считается Я.А. Коменский. Он гениально обосновал, обобщил, углубил и расширил имевшийся уже к тому времени некоторый практический опыт наглядного обучения, применил широко наглядность в практике, снабдив свои учебники рисунками. Коменский в основу познания и обучения поставил чувственный опыт и теоретически обосновал и подробно раскрыл принцип наглядности, называя его «золотым правилом» дидактики [2, с. 22].
Дальнейшее развитие принципа наглядности в обучении встречаются в трудах Г. Песталоцци, И.Ф. Гербарта, А. Дистервега, К.Д. Ушинского и других психологов, педагогов и методистов.
В условиях модернизации системы образования, интенсивно развивающихся компьютерных технологий, доминирования «экранной культуры» приобретения информации, появления новых областей знаний, возрастания объема и скорости информации, перехода от процесса преподавания к процессу учения содержание понятия «наглядность» подверглось значительному изменению, в соответствии с этим изменились и средства наглядности, методы их применения, и даже требования к применениям.
Под наглядностью понимается «широкое использование зрительных ощущений, восприятий, образов, а также постоянная опора на свидетельства органов чувств, благодаря которым достигается непосредственный контакт с действительностью при обучении и воспитании человека». [3]
«Не исключено, что скоро обучаемым предложат изучать виртуальный мир, который позволит получать ощущения, ничем не отличающиеся от ощущений реального мира. Мы можем определять плотность вещества, не пользуясь реальными предметами, а в виртуальной физической лаборатории мы можем «посмотреть» на Землю из иллюминатора космической станции в режиме online. Более того, мы можем «ощутить» то, что в принципе не дано нашей сенсорной системе: сможем совершить путешествие по кровеносной системе человека, посмотреть на нашу галактику и на атом со стороны. При этом можно будет «потрогать» эритроциты, электроны и планеты. В таких условиях проблему наглядности можно было бы считать решенной» [4] на уровне ощущения, восприятия и понимания. Но все же проблема наглядности в таком чувственном познании реальностей, процессов и явлений с помощью высокомощных технологических средств, в плане развития мышления, особенно пространственного, осталась бы не решенной. Да и «неоправданное преувеличение роли виртуальной формы предъявления материала идет во вред содержанию и целям обучения, негативно сказывается на эффективности всего педагогического процесса» [5, с. 253].
При исследовании проблемы развития и формирования пространственного мышления невозможно обойти стороной вопрос применения наглядности в геометрических дисциплинах. Проблема наглядности в развитии и формировании пространственного мышления в геометрии рассмотрена в научных исследованиях Г.Д. Глейзера [6], И.Я. Якиманской [7], В.А. Далингера [8], И.Я. Каплуновича [9], Р.Ф. Мамалыги [10], Е.И. Саниной [11], Ефремовой Д.Д. [12] и др. Ими установлены роль и место наглядности, классифицированы средства, разработаны принципы создания, разборки и использования ее, предложена реализация принципов наглядности в формировании пространственного мышления обучающихся. В наших [13–15] работах показана роль медиасредств и изображений геометрических фигур в развитии пространственного мышления студентов-математиков.
Выяснению роли, места и функции наглядности при формировании пространственного мышления студентов на основе геометрических понятий в современном образовательном процессе посвящено немного работ. Здесь мы попытаемся показать место наглядности в развитии пространственного мышления студентов-математиков при формировании таких понятий, как поверхности второго порядка.
Материалы и методы исследования
Студенческий возраст психологами (Б.Г. Ананьев, В.Т. Лисовский, Л.Д. Столяренко, И.А. Зимняя, С.Д. Смирнов и др.) характеризуется достижением наивысших результатов, быстрой реакцией на внешние раздражители, наивысшей скоростью и большим объемом оперативной памяти, быстрым переключением внимания, умением решать различные задачи и выполнять задания разного уровня, формированием самости, развитием способности принятия ответственных решений и т.д.
Высшее образование оказывает огромное влияние на психику человека, развитие его личности. За время обучения в вузе, при наличии благоприятных условий, у студентов происходит развитие всех уровней психики, меняется вся структура личности в связи с вхождением в новые, более широкие и разнообразные социальные общности. Они определяют направленность ума человека, т.е. формируют склад мышления, который характеризует профессиональную направленность личности [16, с. 422]. Поэтому крайне необходимо оптимально использовать настоящее время для успешного обучения, воспитания, развития и формирования личности студента и его профессиональной подготовки. И этому, в первую очередь, способствует грамотно организованный учебный процесс, соответствующий возрастному и индивидуальным особенностям, а также потребностям студента.
В профессиональной подготовке студентов, помимо методической, психолого-педагогической, предметной, компьютерной, необходимо сформировать и их мышление, в том числе пространственное, что требует умения создания пространственных образов, оперирования ими и правильной ориентации в пространстве.
По предположению И.Я. Каплуновича в студенческие годы «действительно заканчивается дифференциация основных подструктур пространственного мышления (топологический, проективный, порядковый, метрический, алгебраический), но не развитие в целом. Здесь продолжается процесс дифференциации, но не самих подструктур, а внутри них. Также идет процесс интеграции основных подструктур, который обеспечивает наличие высшего уровня развития пространственного мышления» [17].
Результаты исследования и их обсуждение
Студенты со многими объектами вузовского курса геометрии (прямая, плоскость, сфера, вектор, парабола, сечения и т.п.) уже знакомы со школы. Имеют представления о них, умеют воссоздать их образы и оперировать ими. Кроме того, для современных студентов в эпоху развития информационных потоков уже давно преподаватель не является единственным источником информации. При наличии умений и навыков самостоятельной деятельности они способны воспринимать и осваивать теоретический материал, закрепляя его практической деятельностью, при этом обогащая личный опыт приобретения знаний, развивая психические процессы и осуществляя рефлексию.
В постнеклассической дидактике основным дидактическим отношением становится взаимодействие «студент – учебно-профессиональная задача». Соответственно меняются функции преподавателя (от обучения к сопровождению, от отбора учебной информации и организации ее усвоения студентами к систематизации их субъектного опыта); обновляется содержание ведущих дидактических принципов, форм, методов, технологий и т.д. [18]. В таком случае деятельность педагога должна строиться таким образом, чтобы у студента сформировались определенные знания, умения и способности на основе его собственной активности с имеющими знаниями. Однако печально, что некоторые преподаватели до сих пор проводят занятия по традиционной технологии: преподаватель – докладчик, студенты – слушатели; подают готовые знания и оценивают результат выполненных заданий репродуктивного уровня, при этом забывают, что педагогу всего лишь остается грамотно организовать учебный процесс, направлять, помогать, поддержать студента в формировании способности к самостоятельному приобретению знания.
«Поверхности второго порядка» – один из благодатных разделов аналитической геометрии для развития пространственного мышления студентов. Здесь нужно обозначить, что, так как студенты более успешно умеют представлять по памяти, то при изучении поверхностей второго порядка преподавателю сначала следует предложить им мысленно получить эти поверхности самостоятельно, но при этом нельзя недооценивать их умения при создании новых образов. Например, предложить получить поверхности вращения с помощью мысленного вращения плоской фигуры вокруг определенной оси, а эллиптический параболоид – передвигая одну параболу по другой, и пр. Проводимая педагогическая практика показала, что многие студенты могут выполнить такие простые мыслительные операции, могут начертить похожие изображения и сказать, на что они похожи. Поскольку этот раздел изучается в конце курса, студенты уже умеют оперировать пространственными образами без опоры на материальные и условно графические наглядности. Использование таких наглядностей сразу же в начале занятия считается не целесообразным. Чувственное познание поверхности всего лишь дает первичную информацию о ней, с чем студенты уже знакомы, т.е. готовое изображение поверхности, показанное на интерактивной доске, или показ модели поверхности ознакомит лишь с формой этой фигуры и выполнит не когнитивную функцию наглядности, а интерпретирующую, что не способствует развитию пространственного мышления, а, наоборот, мешает. По С.Л. Рубинштейну, ребёнку очень рано доступно восприятие, распознавание и представление пространственных геометрических объектов [19, c. 380]. Поэтому в таком случае нельзя сказать, что применена наглядность для развития мыслительной деятельности студентов. Вращение материальной модели плоской фигуры вокруг некоторой оси с целью описания полученной поверхности или мыслительное вращение с помощью такой модели считается лишним действием. Такое действие является преимуществом процессов восприятия и памяти, но не пространственного мышления. Конечно, мысленное вращение плоской фигуры вокруг оси считается операцией пространственного мышления, но такая деятельность выражается развитием на низком уровне. Здесь целесообразно с помощью знаково-символьной (формулы) или вербальной (словесного описания) моделей создать условия для представления об изучаемой поверхности, т.е. для создания идеальной модели, и мысленно проанализировать и осмыслить поверхность, с уже имеющимися знаниями. Как утверждает А.Н. Леонтьев, наглядность должна служить внешней опорой внутренних действий, совершаемых учащимися [20]. В таком случае мышление перерабатывает эти представления и информацию, помогая создать идеальную модель изучаемой поверхности. Знаково-символьные средства, как абстрактная форма наглядности, способствуют формированию теоретического мышления, которое в свою очередь обеспечивает развитие пространственного мышления высокого уровня. Такое мышление обеспечивает более ясное понимание и представление о пространствах высшего порядка и неевклидовых пространствах.
В исследования пространственного мышления значительный вклад внесла И.С. Якиманская, разработавшая типы оперирования пространственными образами. Все виды оперирования пространственными образами она свела к трем основным: изменение положения воображаемого объекта; изменение его структуры; комбинации этих преобразований [7, c. 118–120].
В формировании пространственного мышления студентов большая часть заданий должны быть последнего уровня, требующими неоднократных мысленных преобразований.
Проанализируем пример, требующий несколько мысленных операций, и покажем место медиасредств при его решении.
«Найти множество точек, являющихся серединами хорд, выходящих из точки М (2, 0, 1), лежащей на эллипсоиде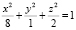 
». При решении этой задачи из точки М мысленно неоднократно придется осуществлять поворот хорды, которая изменит свою длину и положение в эллипсоиде. В результате множество середин таких хорд создадут новый эллипсоид, расположенный внутри данного эллипсоида и соприкасающийся с ним в точке М, каноническое уравнение которого 
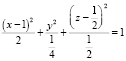. Определение положения вершин и центра по каноническому уравнению полученного эллипсоида – отдельная ментальная деятельность, требующая знания и логики.
Такая проблемная ситуация, созданная преподавателем, является начальным моментом мыслительного процесса, в котором у студента появляется потребность создания нового образа.
В принципе особых проблем при решении такого рода задач без материальных и условно графических наглядностей у студента-математика возникать не должно, здесь главное сформированность умения оперирования пространственными образами и наличие геометрических знаний, какие они имеют на определенном уровне.
При создании образов или оперировании ими педагог не сможет проследить за процессом мыслительной деятельности каждого студента, а всего лишь сможет направлять их мышление в нужное русло, для достижения результата. После мысленного решения данного примера нужно показать не статическую, а динамическую модель с помощью медиасредств, где такая наглядность применяется в целях рефлексии студентов по результату своей мыслительной деятельности. Такая динамическая модель решения рассматриваемого примера более наглядно и легко восприимчива, чем его материальная модель. Таким образом, динамическая модель «позволяют не только закодировать информацию в новую форму, но и визуально передать процесс ее трансформации в пространстве» [21]. Понятие «визуализация» (традиционно трактуемое как психический процесс) предлагается интерпретировать как не только непосредственное зрительное восприятие объекта реальной действительности (распространенная трактовка), но и особый психологический механизм перевода невидимого мыслеобраза (продукта психической деятельности; прообраза) в видимый, зримый образ [22, с. 127].
Современные медиасредства позволяют использовать множество моделей разного уровня сложности, имеющих в условиях интерактивного процесса обучения возможность контроля уровня знаний учащегося (за счет наличия обратной связи), а также подбор вариантов его развития «в ближайших зонах развития» [23]. Несмотря на это, однако, нельзя сказать, что здесь решен вопрос использования наглядности в обучении, всего лишь облегчена деятельность педагога при демонстрации трудно представляемого процесса.
«Каким бы парадоксальным это ни казалось, наиболее адекватным средством наглядности выступает язык математических формул и соответствующих математических понятий» [5, с. 254] для развития пространственного мышления студентов. Такой вид наглядности преследует развивающую цель мыслительной деятельности. Здесь достаточно взаимосвязанных и взаимодополняющих двух кодов передачи информации. В нашем случае знаково-символьный код передачи информации считается основным, а вербальный вспомогательным, но его сопровождение также необходимо. Второй код обеспечивает правильность понимания информации. Эти коды получаются разными органами чувств и выполняют разные функции. Однако третий код передачи информации, например графический, считается уже лишним для развития психологических процессов. Здесь осуществляется процесс перекодирования вербальной и знаково-символьной информации в образную, и наоборот, т.е. идет процесс взаимосогласованной работы обоих полушарий мозга. «Разумеется, мозг функционирует как единое целое, объединяя оба способа организации контекста как взаимодополняющие компоненты мышления. Поэтому чрезвычайно важно развивать оба полушария головного мозга для воспитания гармоничного человека, способного к решению любых самых сложных задач» [24]. Такая способность оказывает существенное влияние на успех профессиональной деятельности при развитии пространственного мышления учащихся общеобразовательной школы.
Таким образом, «весь состав средств обеспечения наглядности по их характеру и значимости в обучении можно распределить на основные и вспомогательные» [25]. В нашем случае знаково-символьные и вербальные наглядности являются основными, а медиасредства вспомогательными.
Выводы
Как мы отметили, С.Л. Рубинштейном установлено, что ребенок очень рано воспринимает конкретную форму предмета, поэтому требовать от студента распознавать и различать геометрические фигуры, создать их образ, изготовить материальные модели, с помощью специальных инструментов графического редактора компьютерных программ получить всего лишь изображение фигур нецелесообразно, так как это отнимает у них время, которого у них и так не хватает на освоение учебных дисциплин, требующих продуктивного мышления. Такие мыслительные и физические деятельности считаются на уровне наглядно-образного и наглядно-действенного мышлений, которые доступны школьнику.
Задания на уровне знания и понимания, например «составить каноническое уравнение эллипсоида по заданным элементам…», не способствуют развитию мышления, здесь всего лишь активизируется память. Поэтому предлагается разработать примеры, задачи и задания, требующие от студента рационального мышления, которое в свою очередь оперирует понятиями, формулами и словесными описаниями изучаемого материала, создавая условие взаимосогласованной работе обоих полушарий, что важно для успешного психического развития.
Преподавателю вуза для развития мышления на занятиях предлагается чаще использовать знаково-символическую и вербальную наглядности, а материальные и условно графические только при необходимости, когда получаемая информация первичная или же если эти наглядности сами являются носителями информации. Динамические компьютерные изображения желательно показывать на стадии закрепления и проверки созданной ментальной модели изучаемого объекта. При использовании наглядности преподавателю необходимо акцентироваться на активизации мыслительной деятельности студента.
По мнению психологов, студенты естественных специальностей отличаются немногословностью, необщительностью и несоциабельностью. Поэтому преподаватель должен принимать во внимание будущую профессию студентов и следить за тем, чтобы у них визуальный канал приема информации не превалировал над вербальным.
Такое организованное обучение не только дает знание предмета, но и обеспечивает развитие пространственного и продуктивного мышлений, рефлексивных навыков, которые способствуют формированию универсальных и профессиональных компетенций будущих учителей математики.