science-review.ru
Современное состояние математического образования в школе показывает, что из разряда лучшего оно перешло на более низкие ступени. Большинство учащихся не усваивают многие вопросы из школьной программы. Явно западают навыки по решению текстовых сюжетных задач, по решению уравнений и неравенств с модулями, по решению уравнений и неравенств с параметрами, по решению нестандартных задач, которые отражены в ОГЭ и ЕГЭ по математике. Слабыми остаются умения и навыки учащихся по владению школьным курсом геометрии (отмечаются несформированность пространственных представлений, низкая логическая культура, неумение доказывать теоремы, неспособность переносить известные факты в измененные ситуации и т.д.).
Причинами столь низкого качества математических знаний, умений и навыков можно назвать слабую мотивированность обучающихся к познанию, нерегулярное выполнение домашних заданий, слабое владение теоретическим материалом и т.д.
Не менее важной причиной такого низкого качества математических знаний, умений и навыков является и используемая учителем технология обучения (арсенал репродуктивных, активных и интерактивных методов обучения, процедура диагностики и оценивания достигнутых результатов учебной деятельности и т.д.).
Цель исследования: ответить на вопрос: «Как следует строить процесс обучения математике, чтобы он задействовал функции как левого, так и правого полушарий головного мозга, иными словами – как создать разумное сочетание логического и наглядно-образного мышления?»
В психолого-педагогической литературе авторы различают стили учебно-познавательной деятельности учащихся и обучающей деятельности учителя.
Опыт учителей, в том числе и наш опыт, показывает, что уровень обученности ученика в учебном процессе напрямую связан как со стилем его учебной деятельности, так и со стилем обучения учителя. Наиболее высокий уровень обученности достигается, когда эти стили совпадают.
Бетти Лу Ливер отмечает, что обучение слабо ориентируется на ученика [1].
А.Г. Мордкович провозглашает два лозунга, относящихся к обучению школьной математике: меньше схоластики и формализма; больше геометрических иллюстраций и наглядности [2].
А.Л. Сиротюк отмечает, что школьные методики в основном развивают левое полушарие головного мозга.
При использовании когнитивно-визуальной технологии обучения математике реализация принципа наглядности в обучении получает новое решение: язык наглядных образов математических объектов становится и предметом познания, и средством обучения.
Известный математик Д. Гильберт отмечал, что приоритетными должны быть тенденция к наглядности, стремление к живому пониманию объектов и их внутренних отношений.
Центральным компонентом когнитивно-визуальной технологии являются визуализированные задачи (подробный анализ использования визуализированных задач представлен в работах [3, 4]).
Основу визуального поиска предоставляет чертеж, который должен быть верным, наглядным, легко выполнимым.
В когнитивно-визуальной технологии наглядность может использоваться как явно, так и неявно.
Покажем на двух задачах явное и неявное использование наглядности.
Задача 1. Длина ребра куба ABCDA1B1C1D1 равна 2 см. Пусть М – точка окружности S1 , вписанной в квадрат ABCD, а N – точка окружности, проходящей через вершины А, В1 , С. Найдите наименьшее расстояние между ними.
Эта задача имеет замечательно красивое, но трудно находимое геометрическое решение. В литературе приводится аналитическое решение, основанное на условной оптимизации. Опишем начальный шаг авторского решения.
Введем пространственную систему координат следующим образом: начало координат О поместим в центр куба, положительные полуоси Ox, Оу, Oz направим проходящими соответственно через грани AA1D1D, DD1B1C, A1B1C1D1 перпендикулярно им. Тогда имеем А = (1; –1; –1), В1 = (–1; –1; 1), С = (–1; 1; –1). Проходящая через эти точки окружность является сечением сферы х2 + у2 + z2 = 3 плоскостью х + у + z + 1 = 0. Берутся точки
N = (x; y; z)∈S2,
М = (cos t; sin t; –l)∈S1 (0 ≤ t ≤ 2p) (1)
и минимизируется расстояние между ними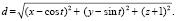 
Беря подкоренное выражение в качестве целевой функции и применяя метод Лагранжа при условиях x + y + z + +1 = 0, x2 + y2 + z2 – 3 = 0, получаем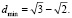 
В предлагаемой статье в решении задачи 1 вместо минимизации функции от четырех аргументов при двух связях она решается как оптимизационная двумерная задача с параметром t при одном уравнении связи, при этом целевая функция линейная по основным переменным. По ходу решения попутно выявляется и величина dmax без обращения к чертежу. Проведенные рассуждения почти дословно переносятся на решение следующей родственной задачи 2.
Задача 2. В том же кубе на лучах А1А, А1В1, A1D1 взяты соответственно точки E,F,G так, что А1Е = A1F = A1G = b. Пусть М – точка окружности S1, вписанной в квадрат ABCD, а N – точка окружности S2, проходящей через E,F,G. Чему равно наименьшее значение длины отрезка MN?
Решение задачи 1
Используя уравнения сферы и плоскости, пересечением которых является S2, представим целевую функцию (квадрат расстояния между N, М) в виде:
u = 3 – 2(l + cos t)x – 2(l + sin t)y,
0 < t < 2p. (2)
Будем исследовать ее на экстремум при связи
g(x, y) = x2 + у2 + (х + у + 1)2 – 3 = 0. (3)
Геометрически задача сводится к тому, чтобы при всяком фиксированном значении параметра t среди линий уровня и = const (прямых) выбрать те, которые касаются графика уравнения связи g(x, y) = 0 (эллипса), и точки касания проверить на нужную оптимальность.
Потребуем, чтобы градиент функции Лагранжа L = u + λg по х, у был нулевым. Из равенств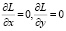 
получим систему:
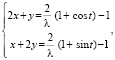
откуда
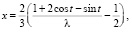
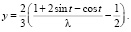(4)
При таких х, у из уравнения связи (3) получим:
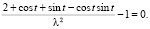
Заметим, что здесь числитель дроби не меньше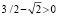 
, так что:
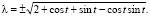
При указанных выше х, у как функций параметра получим следующее выражение через него целевой функции:
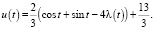
Заметим, что второй дифференциал функции Лагранжа d2L = 2l(dх2 + + dxdy + + dy2) является знакоопределенной квадратичной формой. Она положительно определенная, если множитель Лагранжа положительный, поэтому указанное выше значение целевой функции минимальное; при смене знака имеем максимум. На этом применение метода Лагранжа и закончилось. Остается исследовать функцию u(t) отрезке [0; 2p] на минимум при l > 0 и на максимум при l < 0. Анализ этой функции на экстремум технически затруднителен, поэтому введем еще параметр р = cos t + sin t. Имеем: t∈[0, 2p] ⇒ р∈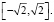
Тогда
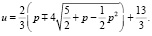
Рассмотрим случаи знаков множителя Лагранжа.
1. l > 0. Оптимизационная задача
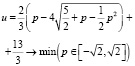
имеет единственное решение во внутренней стационарной точке отрезка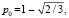 
при этом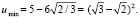 
2. l < 0. Задача
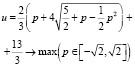
имеет решение на границе: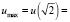 
.
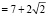Осталось указать точки окружностей, между которыми расстояния экстремальные. Для этого подберем какой-нибудь угол t так, что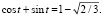 
Рассмотрим точки в R3
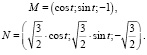
Они лежат соответственно на окружностях S1, S2, и расстояние между ними равно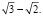 
Наибольшее расстояние между точками окружностей достигается при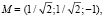 
N = (–1; –1; 1) и равно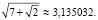 
Заметим, что в решении задачи 1 наглядность использовалась неявно.
Решение задачи 2
Предполагаем, что b > 0. При указанном выше выборе системы координат имеем E = (1; –1; 1– b), F = (1 – b; –1; 1), G = (1; –1 + b; 1). На этот раз окружность S2 является пересечением поверхностей х2 + у2 + z2 – – 2 – (b – – 1)2 = 0, x – y + z + b – 3 = 0. Берем точки согласно (1) и будем находить не только наименьшее, но и наибольшее расстояние между ними. Целевая функция строится аналогично и имеет вид:
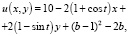
уравнением связи будет g(x, y) = х2 + + у2 + (–х + у + 3 – b)2 – 2 – (b – 1)2 = 0. Аналогами равенств (4) станут:
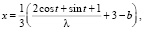
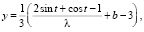(4а)
множителями Лагранжа будут l = ±(2 + + cos t sin t – sin t + cos t)1/2 / b. При этом значение целевой функции в точке (4а):
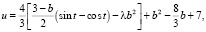
а второй дифференциал функции Лагранжа имеет вид d2L = 4l(dх2 – dxdy + + dy2). Введем параметр р = sin t – cos t и будем исследовать функции:
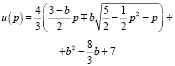(5)
соответственно на минимум и на максимум на отрезке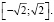 
Согласно знакам в (5) стационарная точка как функция параметра b имеет вид:
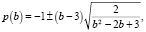
соответствующие графики представлены ниже. Несложные выкладки дают значение целевой функции в ней: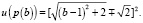 
Снова рассматриваем случаи знаков множителя Лагранжа.
1. l > 0, т.е. в (5) берем знак «минус». Из двух значений целевой функции на концах отрезка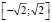 
наименьшим является 
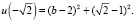Нетрудно проверить, что 
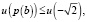причем знак равенства имеет место лишь при 
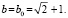Такое значение параметра является критическим в том смысле, что при b < b0 стационарная точка покидает отрезок, иначе остается на нем. Этой ситуации соответствует левый чертеж на предлагаемом ниже рисунке.
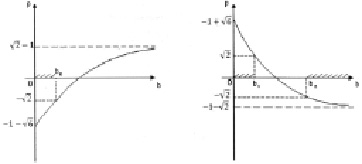
К задаче 2
Следовательно,
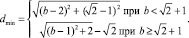(6)
2. l < 0. На этот раз имеем значения на границе
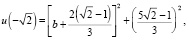
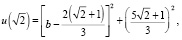(7)
при этом:
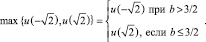
Непосредственно проверяется, что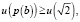 
причем знак равенства имеет место лишь при 
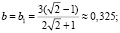аналогично 
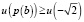, и равенство возможно только при 
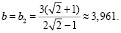Эти значения также критические: при b < b1 или b > b2 стационарная точка p(b) покидает отрезок (см. правый чертеж на рис. (зона «покидания», как и на левом чертеже, помечена штриховкой)).
Следовательно,
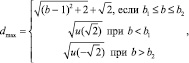(8)
где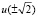 
находятся согласно формулам (7). Здесь верхнее выражение согласуется с тем, что расстояние между точками двух концентрических сфер не более суммы их радиусов, причем равенство достижимо. Например, при b = 2 найдем какое-нибудь решение уравнения 
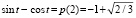и положим:
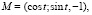
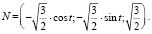
Расстояние между этими точками равно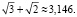 
Заметим, что равенства (6), (8) верны и при b = 0. В этом случае (сделаем чертеж!) окружность S2 вырождается в точку А1, наименее удаленная от нее точка N1 окружности S1 лежит на диагонали АС на расстоянии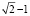 
от А, наиболее удаленная N2 – на расстоянии 
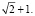По теореме Пифагора:
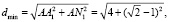
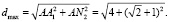
Но точно такие же расстояния получаются и по формулам (6), (8).
Заметим, что в решении задачи 2 наглядность использовалась явно.
Читателю, проявившему интерес к рассматриваемой проблеме, небезынтересным будет знакомство с содержанием статей [5–7] и книги [8].