Оценка качества винных изделий является не простым процессом без проведения специальных лабораторных тестов и экспертных дегустаций. Применение методов интеллектуального анализа данных в винодельческой отрасли позволит значительно облегчить процесс определения качества вина.
Благодаря тому, что за последние несколько лет были разработаны многочисленные библиотеки с открытым исходным кодом и мощные алгоритмы, позволяющие обнаруживать в данных повторяющиеся образы, стало возможным делать прогнозы о будущих событиях.
Таким образом, основываясь только на наборе химических показателей, классификация качества винных изделий будет производиться без участия экспертов.
Постановка задачи и описание набора данных
Основной целью данной работы является разработка программного продукта для классификации экспертных сенсорных оценок качества винных изделий на основе физико-химических тестов.
Для исследования предметной области использовался набор данных белого португальского вина «Vinho Verde» [1], взятый из общедоступного хранилища UC Irvine [2].
Этот набор данных содержат 3298 уникальных экземпляров белого вина с 11 физико-химическими характеристиками, такими как:
1 – фиксированная кислотность (fixed acidity);
2 – летучая кислотность (volatile acidity);
3 – лимонная кислота (citric acid);
4 – остаточный сахар (residual sugar);
5 – хлориды (chlorides);
6 – свободный диоксид серы (free sulfur dioxide);
7 – общий диоксид серы (total sulfur dioxide);
8 – плотность (density);
9 – pH;
10 – сульфаты (sulphates);
11 – алкоголь (alcohol).
Кроме этого, эксперты в ходе дегустации оценили качество вина от 0 (очень плохо) до 10 (очень хорошо). Усредненные сенсорные оценки по каждому примеру содержатся в этом же наборе данных.
Практическая реализации
Этапы практической реализации заключаются в следующем:
I. В интерактивной оболочке Jupyter Notebook [3] подключаются необходимые библиотеки [4] интеллектуального анализа данных.
II. Набор данных представлен в файле формата *.csv. Он загружается в оперативную память.
III. Переменной Y присваивается вектор со всеми значениями сенсорных оценок, значения остальных признаков записываются в переменную Х.
IV. После того как данные загружены необходимо провести качественный анализ.
Анализ данных
Авторами проведен статистический анализ данных на основе имеющегося набора и были определены минимальное, максимальное, среднее и стандартное отклонение значений всех экземпляров для каждого примера, которые представлены в таблице.
Статистические данные по набору
|
Признак |
Мин. |
Макс. |
Ср. знач. |
Ст. откл. |
|
Fixed acidity (г\дм3) |
3.800 |
14.20 |
6.855 |
0.842 |
|
Volatile acidity (г\дм3) |
0.080 |
1.100 |
0.278 |
0.100 |
|
Citric acid (г\дм3) |
0.000 |
1.660 |
0.333 |
0.121 |
|
Residual sugar (г\дм3) |
0.600 |
65.80 |
6.406 |
5.108 |
|
Chlorides (г\дм3) |
0.009 |
0.346 |
0.046 |
0.021 |
|
Free sulfur dioxide (мг\дм3) |
3.000 |
289.0 |
35.33 |
17.16 |
|
Total sulfur dioxide (мг\дм3) |
9.000 |
440.0 |
138.4 |
42.99 |
|
Density (г\см3) |
0.987 |
1.039 |
0.994 |
0.003 |
|
pH |
2.740 |
3.800 |
3.188 |
0.150 |
|
Sulphates (г\дм3) |
0.220 |
1.080 |
0.490 |
0.114 |
|
Alcohol ( %) |
8.000 |
4.200 |
10.52 |
1.237 |
|
Quality |
3.000 |
9.000 |
5.877 |
0.890 |
Исходный набор не содержит отрицательных значений и пропусков, а также ни один из винных экземпляров не получил оценку ниже 3 или выше 9, поэтому сформировано 7 классов качества.
Архитектура нейронной сети
Модель нейронной сети представляет собой многослойный персептрон, схематично изображен на рис. 1.
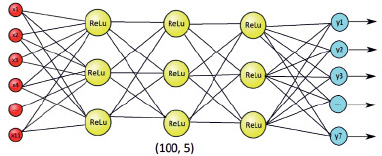
Рис. 1. Архитектура многослойного персептрона
Входной слой обозначен красным цветом и включает 11 входных параметров, перечисленные в первом столбце таблицы. Определение количества скрытых слоев и нейронов в них зависит от показателя точности (accuracy). Опытным путем установлено, что 5 скрытых слоев по 100 нейронов каждый является оптимальным, в противном случае будем иметь более низкие показатели обучаемости сети. Последний слой, синий, состоит из 7 выходных значений классов качества.
Существует несколько методов обучения нейронной сети и в нашей задаче будет использоваться алгоритм обратного распространения ошибки, который использует стохастический градиентный спуск (SGD) [5] в качестве алгоритма оптимизации. Функцией активации нейронов выступает выпрямленная линейная функция (ReLU) [6]. На рис. 2 изображена часть программного кода, необходимая для реализации обучения нейронной сети.

Рис. 2. Пример программного кода для обучения нейронной сети
Для оценки точности работы используемого алгоритма применяется такая метрика, как достоверность.
Оценка точности алгоритма
Достоверность (accuracy) – это доля выборки, по которым классификатор принял правильное решение. Достоверность считается по формуле:
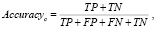 (1)
(1)
где Accuracyc – достоверность c-го класса, TN – истинно-отрицательное решение, TP – истинно-положительное решение, FP – ложно-положительное решение, FN – ложно-отрицательное решение [7].
Для оценки точности работы алгоритма исходный набор данных был случайным образом разделен на обучающую и тестовую выборку в соотношении 7:3 соответственно.
Обучив модель нейронной сети и протестировав ее на данных второй выборки получился следующий результат: accuracy=0.453532. Для повышения accuracy можно пытаться подобрать более удачные гиперпараметры или воспользоваться другим алгоритм.
Заключение
В ходе решения поставленной задачи была спроектирована и обучена модель нейронной сети, проведено испытание на тестовой выборке и получена оценка точности алгоритма.
Таким образом, можно заключить, что на прирост точности влияют множество факторов и нюансов, для этого изначально рекомендуется качественно исследовать набор данных, связи между различными признаками, корреляцию. Это позволит лучше понять данные, с которыми предстоит работа и в перспективе найти оптимальную модель обучения.
Данная работа выполнена в рамках курсового проекта по дисциплине «Методы интеллектуального анализа данных», научный руководитель – д.ф.-м.н., профессор Воронова Л.И.


 science-review.ru
science-review.ru