science-review.ru
Во все времена люди имели потребности во благах. В современном мире в связи с увеличивающимися потребностями населения появляется необходимость в расширении рынка товаров и услуг, что влечет за собой развитие экономической науки.
Экономика – это наука, которая изучает, как люди использует имеющиеся ограниченные ресурсы для удовлетворения своих неограниченных потребностей в жизненных благах [1].
Экономика призвана ответить на три основных вопроса:
– какие товары и услуги надо производить и в каком количестве;
– каким образом и с помощью каких ресурсов будут произведены товары и услуги;
– для кого производить услуги и товары.
Несмотря на то, что экономическая наука существует не одно столетие и имеет большую теоретическую базу, она не в силах предвидеть изменения в будущем и дать точные прогнозы. Это связано с тем, что многие экономические показатели носят характер случайных отклонений. Поэтому чтобы экономистам рассчитать наиболее выгодный вариант с высокой точностью, необходимо применять знания теории вероятностей.
Теория вероятностей – наука, изучающая закономерности в массовых случайных событиях. Случайным событием называют какой-либо факт, который может произойти или не произойти при определенной совокупности условий. Совокупность всех условий, при которых наблюдается то или иное событие, определяется как опыт или эксперимент [2].
Вероятность рассматривают как некоторый критерий возможности наступления определенного события. Возможные значения вероятностей изменяются в диапазоне от 0 до 1. Событие, вероятность появления которого равна 0, называется невозможным, то есть это событие никогда не произойдет при заданных условиях. Событие с вероятностью, равной 1, считают достоверным, речь идет о событиях, которые обязательно произойдут при данных условиях [3].
События, одно из которых обязательно произойдет в результате опыта, составляют полную группу. Сумма значений вероятностей наступления событий из полной группы равна единице. Например, если вероятность увеличения цены товара в ближайший месяц равна 0,3, а вероятность того, что цена останется неизменной – 0,65, вероятность уменьшения цены несложно найти. Так как эти события составляют полную группу (одно из них обязательно произойдет), то вероятность того, что цена товара уменьшится, равна 0,05, так как 1-0,3-0,65 = 0,05 [4].
Сумма вероятности наступления события и вероятности того, что оно не произойдет, также равна 1. Так как возможен только один из вариантов: наступит событие или нет.
На практике мы имеем дело с независимыми событиями, то есть одно событие не влияет на появление другого, и зависимыми, когда наступление событий взаимосвязано.
Для решения задач используют формулы сложения вероятностей, когда необходимо найти вероятность появления хотя бы одного события, и формулу умножения вероятностей, если важно совместное наступление событий.
При решении задач с независимыми событиями мы работаем с вероятностями появления одного или нескольких события вне зависимости от других. Бывают ситуации, когда необходимо найти вероятность наступления определенного количества событий.
Рассмотри задачу с независимыми событиями. Две организации производят одинаковую продукцию. Вероятность того, что АО «Стройка» выйдет ни мировой рынок, равна 0,6, а вероятность выхода на мировой уровень ПАО «Стройоптторг» равен 0,7. Найти вероятность того, что только одна организация выйдет на мировой рынок [5.6].
Для решения этой задачи отметим события, о которых говорится в задаче:
А – событие, что АО «Стройка» организация выйдет на мировой рынок,
В – событие, что ПАО «Стройоптторг» организация выйдет на мировой рынок.
Имеем дело с событиями:
А1 – событие, что АО «Стройка» организация выйдет на мировой рынок, при этом ПАО «Стройоптторг» не выйдет на мировый рынок,
В1 – событие, что ПАО «Стройоптторг» организация выйдет на мировой рынок, а АО «Стройка» не выйдет на мировой рынок.
Определим вероятности этих событий:
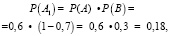
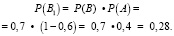
Теперь найдем сумму этих вероятностей, так как нам не важно, какое именно событие из двух произойдет:
.
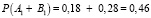Ответ: вероятность того, что только одна из организаций выйдет на мировой рынок, равна 0,46.
Часто вероятность наступления события зависит от другого события. Если событие А может произойти только вместе с одним из других событий (Н1, Н2, …, Нn), образующих полную группу, то формула нахождения вероятности будет выглядеть следующим образом:
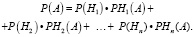
Эта формула называется формулой полной вероятности, а события H1, H2, …, Hn – гипотезы [2].
Приведем пример экономической задачи, решаемой с помощью формулы полной вероятности. Экономист полагает, что вероятность роста стоимости акций некоторой компании в следующем году будет равна 0,75, если экономика страны будет на подъеме; и эта же вероятность будет равна 0,3, если экономика страны не будет успешно развиваться. Вероятность экономического подъема в новом году равна 0,8. Оценить вероятность того, что акции компании поднимутся в цене в следующем году [2].
Для решения этой задачи необходимо выбрать события, о котором идет речь в задаче:
А – событие, что акции компании в следующем году поднимутся в цене.
Далее мы определяем гипотезы:
H1 – гипотеза, что экономика страны будет на подъеме,
H2 – гипотеза, что в стране не будет успешного развития экономики.
Определим вероятности гипотез:
P(H1) = 0,8 (по условию); P(H2) = 1 – 0,8 = 0,2, так как эти события образуют полную группу.
Из условия известны вероятности наступления события при выполнении гипотез:
.
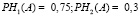Применив формулу полной вероятности, найдем вероятность повышения цены акций компании в следующем году:
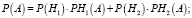
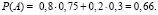
Ответ: вероятность того, что акции компании в следующем году увеличатся в цене, равна 0,66.
Также в экономической практике приходится работать с последовательностью событий, вероятность которых не зависит от наступления других. Вероятность наступления таких событий вычисляется по формуле Бернулли [7]:
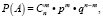
где n – общее число исходов,
m – число благоприятных исходов,
p – вероятность наступления благоприятного исхода,
q – вероятность наступления противоположного исхода,
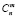– количество способов выбора комбинации, в которую входит необходимое сочетание благоприятных и противоположных им событий.
Пример экономической задачи, решаемой с помощью формулы Бернулли. В городе 10 коммерческих банков. У каждого риск банкротства в течение года составляет 10 %. Чему равна вероятность того, что в течение года обанкротится больше одного банка? [2].
В данной задаче можно выделить 11 событий: событие, что обанкротятся 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 банков. Все эти события составляют полную группу, так как обязательно произойдет одно из них. Следовательно, сумма вероятностей всех событий равна 1. Таким образом, чтобы ответить на вопрос задачи, можно найти вероятность, того что обанкротится 1 банк и вероятность того, что не один банк не обанкротится, и вычесть их сумму из единицы .
Определим события, которые мы будем рассматривать:
А – событие, что в течение года обанкротится больше одного банка,
В – событие, что в течение года не один банк не обанкротится,
С – событие, что в течение года обанкротится 1 банк.
Мы выяснили, что
.
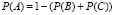Воспользуемся формулой Бернулли для нахождения вероятности события B, подставив нужные значения [8]:
n = 10, так как всего рассматривается 10 банков;
m = 0, так как мы рассматриваем вариант, что не один банк не обанкротится;
p = 0,1, так как в условии сказано что вероятность события, что банк обанкротится равна 10 % ( 10 % от 1 – 0,1);
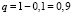– вероятность, что банк не обанкротится.
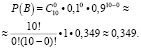
Теперь найдем вероятность события C. В этом случае переменные принимают следующие значения: n = 10, m = 1, p = 0,1, q = 0,9.
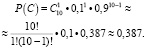
Найдем вероятность события A:
.
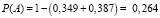Ответ: вероятность того, что в течение года обанкротятся больше одного банка, равна 0,264.
Мы рассмотрели некоторые случаи применения теории вероятностей при решении экономических задач. На практике экономисты часто сталкиваются с задачами, для решения которых необходимы знания теории вероятностей [9, 10].
Таким образом, экономика тесно переплетается с математическими науками, теория вероятностей не является исключением. Данный раздел математики широко используется в экономике, помогает рассчитать возможность успеха или неудачи с максимальной точностью. Поэтому можем сказать, что экономистам необходимы знания теории вероятностей для применения в своей профессиональной деятельности, что поможет повысить эффективность экономики.