science-review.ru
Само понятие «корреляция» в такой науке, как математическая статистика появился недавно. Основной вклад в изучении этого понятия внесли английские учёные в середине XIX, Френсис Гальтон и Карл Пирсон. Именно этот показатель позволяет получить ответы на интересующие всех вопросы, может ли быть какая-либо связь между случайно выбранными показателями (например, между прибылью и объемом продаж), либо между совершенно разными показателями (например, при исследовании нескольких предприятий). Также определяется зависимость, если эта связь действительно возможна, то зависит ли повышение одного показателя увеличением другого.
Во всех сферах экономической политики происходит регулирование тех или иных определенных экономических параметров. Поэтому такое управление должно учитывать влияние таких параметров на различные экономические среды [1].
Связь какого-либо одного из показателей с другими описывается с помощью функций одной y = f(x) или нескольких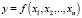 
переменных.
На различные экономические ситуации влияют множество различных ситуаций, существующих в действительности. Эти ситуативные факторы не определяются чётко в модели. Они не могут быть выражены количественно и выбираются абсолютно случайно. Также с помощью этих факторов происходит варьирование реальных данных. Возможно также их несовпадение с величинами, рассчитанными по формуле связи переменной с объясняющими признаками [2].
Приведённые выше данные показывают, что не всегда возможность учитывать эти показатели в корреляционной модели себя оправдывает. Такая модель получается очень объёмной и многие из фактов, которые там используются, влияют на модель в меньшей степени, чем другие. С учётом приведённых данных, можно увидеть, что в корреляционную модель включаются только те, которые в наибольшей степени на нее влияют.
Отбор элементов делится на несколько этапов. При самом первом применяется метод качественного анализа, который, в свою очередь, дополняетсясопоставлением числовых и количественных данных [3].
На предприятии очень часто необходимо исследовать производство, поэтому актуальным становится изучение зависимостей в производстве. Зависимость такого рода функций, которые основываются на данном анализе, описывают соотношение между показателями деятельность в сфере производства предприятия: объемом выпускаемой продукции, издержками на капитал, фондоотдачей, производительностью труда и т.д. Объема производства осуществляется по формуле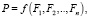(1):
(1)
где Р – объем производства;
F – факторы, определяющие величину выпуска – затраты ресурсов: труда, основных средств, сырья, материалов.
Примером практического использования методов корреляционного анализа может служить решение следующей задачи: необходимо проанализировать финансовое состояние предприятия с учётом факторов, влияющих на наличие необходимых предприятию ресурсов. На РПУП «Торгмаш» основными источниками, определяющими их формирование, являются собственные оборотные средства.
В результате проведения исследования финансовых показателей предприятия было выявлено, что на РПУП «Торгмаш» существует необходимость в собственных оборотных средствах. Всё это влияет на сокращение использования финансовых возможностей и в дальнейшем ведет к шаткому финансовому состоянию предприятия.Для выяснения причин проводятся экономические исследования, цель которых будет состоять в выявлении показателей, таких как – кредиторская задолженность и сумма оборотных активов, влияющих на изменения потребности в собственных оборотных средствах РПУП «Торгмаш».
Поверхностная плотность у, г/м2 является одним из важнейших параметров определения структуры трикотажа, который обусловливает расход полотна на единицу изделия. Необходимо определить аналитическую зависимость поверхностной плотности у трикотажа платированных футерованных переплетений, вырабатываемого на крутовязальной машине модели FIHN фирмы «Орицио», от длины нитей в петлях при следующих заправочных данных: грунтовая и платированная нити – хлопчатобумажная пряжа линейной плотностью 18,5 текс, футерованная нить – хлопчатобумажная пряжа линейной плотностью 72 текс, раппорт кладки футерной нити Кф = 1 + 3 с расположением ее со сдвигом.
В качестве факторов приняты: xг – суммарная длина нитей в платировочной/n и грунтовой 1Г петлях, /n + 1 мм; x2 – соотношение длин нитей в петле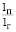 
; x3 – длина футерной нити /ф, мм. Полотна предварительно приводились в условно равновесное состояние путем стирки.
Множественная корреляция является выражением данной зависимости. Также существует возможность выражения криволинейной функции выпуска продукции, которое осуществляется по следующему уравнению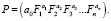(2):
(2)
Есть также возможность для каждой возникшей ситуации определить абсолютную скорость. С помощью этого показателя осуществляется взаимодействие величин в пределе между увеличением объёма выпуска продукции с ростом затрат на данный ресурс. Эта абсолютная скорость определяется как частная производная выпуска продукции по затратам данного вида ресурса и рассчитывается по следующей формуле 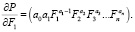(3):
(3)
Величина всех показателей уравнения влияет на абсолютную скорость элементов корреляционной связи, т.е. влияет на показатели между всеми ресурсами и выпуском продукции [4].
Относительная скорость также как и абсолютная является не менее важным показателем для подсчёта экономических величин. Она показываеткак влияет увеличение затрат производства на 1 % на выпуск продукции. Относительная скорость изменения объема выпуска продукции от изменения затрат на 1 % называется эластичностью выпуска по затратам и обозначается символом «Е» и рассчитывается по формуле (4):
Ei = ai. (4)
В качестве функции, показывающей выпуск продукции используется уравнение (2). С учёт этого уравнения мы видим, что эластичность выпуска является величиной постоянной для каждого фактора и приравнивается соответственно коэффициенту регрессии. Иными словами, при любом объеме затрат и выпуска продукции, увеличение затрат n-го вида ресурсов на 1 % ведет к увеличению выпуска продукции на «а», %.
Также немало важными показателями являются не только абсолютная и относительная скорость, но и средняя и предельная эффективность выпуска продукции [5].
Предельная эффективность для линейных и логарифмических функций определяется как частная производная конечного продукта по объему ресурса. Для n-го ресурсаэффективность, может быть, рассчитала по такой же формуле, как и абсолютная скорость (3).
Средняя эффективность выпуска по отношению использования первого ресурса определяется отношением и записывается в виде следующей формулы 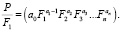(5):
(5)
Из вышеперечисленного можно сделать вывод, что предельная эффективность использования ресурсов всегда оказывается ниже средней, так как при ax > 1 уравнение (3) меньше уравнения (5). Это справедливо и для всех других ресурсов.
Производственные функции кроме того могут принимать вид модификаций уровня производительности труда. Отличают два типа данных модификаций: первая демонстрирует отличия в степенях производительности труда между фирмами, отпускающими однородную продукцию. Здесь устанавливают взаимозависимость среди подобных факторов, как объем производства, размер и структура производственных фондов, степень специализации, энерговооруженность труда, продолжительность производственного цикла и другие [6].
Корреляционный анализ кроме того способен проводиться и в функциях спроса и предложения. На функцию спроса в большей степени могут воздействовать подобные факторы, как прибыли потребителей, уровень стоимости, а кроме того количественный состав семей. Значимым показателем, демонстрирующим взаимосвязь между доходами покупателей, считается коэффициент эластичности [7].
Обозревание нормативов считается возможностью применения корреляционного анализа. В этом случае с помощью представленного анализа возможно аргументировать уровень косвенных издержек в себестоимости продукта. В случае если анализировать прямые расходы, то они как правило разбираются с точки зрения промышленных характеристик изготавливаемого продукта и с применением установленной технологии его производства, в таком случае размер непрямых издержек обусловливается под влиянием разных факторов разной степени трудности. Кроме того имеется корреляционная многофакторная модель, которая подразумевает отбор наиболее значительных из моделей.
Нормирование количества персонала также считается важным элементом при применении корреляционных моделей. Число оснащения и рабочих мест в компании непосредственно находится в зависимости от количества основных рабочих. Если же у руководства появляется необходимость в найме обслуживающего и дополнительного персонала, становится видно отсутствие точных критериев. В то время нормативы формируются свободно. Вследствие применения корреляционных моделей делается допустимым установить среднюю численность работников по ремонтным работам и наладке оснащения, вспомогательных работников, разных категорий административно-управленческого персонала в зависимости от главных показателей. Может производиться оценка тесноты корреляционной связи между признаками. Для этого в аналитических группировках межгрупповую дисперсию δ соизмеряют с общей а. Это отношение называется корреляционным и обозначается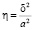 
.
Данная величина характеризует факторный признак, положенный в основание группировки, который вызвал долю вариации результативного признака. Корреляционное отношение по своему абсолютному значению колеблется в пределах от 0 до 1. Чем сильнее факторный признак оказывает влияние на результативный, тем ближе корреляционное отношение к 1. Также можно увидеть и полное отсутствие корреляционной связи, когда факторный признак не влияет на результативный. В таком случае вариация, обусловленная им, будет равна нулю δ2 = 0 и корреляционное отношение также равно нулю.
Вариация, обусловленная изменением результативного признака, происходящего под воздействием какого-либо факторного признака, равна общей вариации δ2 = a2 и корреляционное отношение будет равно единице η2 = 1, что говорит о наличии полной связи.
Кроме того, вероятна перекрёстная классификация, допускающая организацию исходных данных с двумя и более условиями, в каковых постепенная последовательность одного фактора сочетается с определённым уровнем другого; иерархическая (гнездовая) классификация, в которой установленное множество одного фактора отвечает случайно подобранному значению другого каждому.
Таким образом, владение инструментарными основами статистического анализа в экономических исследованиях подразумевает умение изыскателя грамотно установить и осуществить расчёт данных (такие, например, как коэффициент корреляции), которые отображают цели, проблемы, а также необходимости проводимого исследования. Кроме того предполагает возможность абсолютно точно толковать результаты исследуемых действий и, в случае если появляется потребность, дополнить либо же отредактировать установленные итоги проведённого исследования. Применение статистических, а кроме того математических способов предоставляет возможность проверки, анализа, а также объяснения необходимости использования тех или иных методов исследования определенного экономического объекта в установленных ситуациях.