science-review.ru
Теория вероятностей представляет собой науку, которая направлена на исследование вероятностных событий, явлений, процессов, их свойств, качеств, закономерностей. Всё происходящее на рынках финансов, подпадает под действие принципов и законов данной науки, в силу того, что наибольшее число событий на просторах рынка носит случайный характер. С точностью предопределить результаты сделок и операций на финансовых рынках невозможно, потому что последствия зависят от большого количества факторов, предсказать которые достаточно трудно. В математике вероятность определяется как некий показатель, определяющий – случится ли то или иное событие в будущем, который представляется в числовой форме. Значение данного показателя может варьировать от нуля (т.е. событие точно невозможно), до единицы (когда оно несомненно произойдет). Обычно степень вероятности показывают в процентах. При проведении расчетов с использование теории вероятностей применяются также методы сложения и перемножения, но придерживаясь определенных правил. Данная наука является важным способом предопределения возможности создания связей и взаимоотношений [1, 2].
При изучении такой математической дисциплины, как «теория вероятностей», возникает вопрос о ее применении в жизни человека. В экономической сфере, которая является одной из важнейших сфер жизни общества, данная дисциплина играет немаловажное значение, поэтому она стала неотъемлемой частью в обучении специалистов, таких как экономист и финансист. В частности, для исследования экономических данных используют формулу Бернулли, локальную теорему де Муавра-Лапласа, интегральную формулу Лапласа.
Хотя история теории вероятностей берет своё начало с XIII века, в России она получила развитие лишь в XIX столетии, во время создания Петербургской математической школы. Основными ее представителями были П.Л. Чебышев, основатель школы, А.А. Марков и А.М. Ляпунов. Среди их многочисленных заслуг выделяют: расширение и обобщение закона больших чисел; заложение основы теории случайных, или «стохастических», процессов; разработка специального метода характеристических функций для доказательства центральной предельной теоремы при чрезвычайно общих условиях [3].
Теория вероятностей является наукой, которая занимается исследованием использования характерных методов при рассмотрении задач, появляющихся при анализе случайных величин, раскрывая массовые закономерности. Из данного понятия можно сделать вывод, что, если мы исследуем законы, управляющие случайными событиями, тогда сумеем оказать влияние на процесс наступления данных событий.
В экономической науке имеется достаточное количество экономических показателей, вычисление которых не требует точных значений, а допускает наличие небольших отклонений. Методы теории вероятностей необходимо применять там, где допускается возможным создать и проанализировать вероятностные модели действий либо явлений. Примером могут послужить характеристики в сфере кредитования и страхования [4].
Одной из областей в экономике, расчеты в которой позволяют совмещать использование разнообразных методов теории вероятностей, считается сфера страхования. К примеру, с их помощью становится возможным нахождение вероятности наступления каких-либо страховых происшествий (например, наступление смерти гражданина в зависимости от возраста) [5].
Для более подробного изучения применения теории вероятностей на практике наглядно рассмотрим решение задач в сфере страхования [6].
Пример 1.
Страховая компания N заключила 80000 договоров имущественного страхования. Вероятность наступление утраты, недостачи или повреждения имущества по каждому договору в течение года составляет 4 %. Найти вероятность, что таких случаев будет не более 4000.
Решение. По условию задачи n = 80000 (было заключено 80000 договоров), p = 0,04 – вероятность наступления страхового случая.
Находим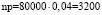 
. Для того, чтобы рассчитать Р(m ≤ 4000) необходимо использовать интегральную теорему Муавра-Лапласа, которая имеет следующий вид:
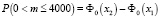
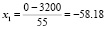
и
,
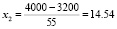которые находятся таким образом:
; 
.
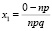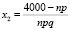По таблице Ф(x1) = 0,5, при x1 = –58,18, Ф(x2) = 0,5, при x2 = 14,54.
Находим по таблице значений функции Лапласа:
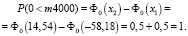
На основании проведенных расчетов можно сказать, что вероятность того, что страховых случаев будет не более 4000, составила 1.
Помимо решения задач в сфере страхования рассмотрим применение теории вероятностей в решении задач, затрагивающих кредитную сферу [7].
Пример 2.
Курс акции, выпущенных кредитной организацией K, в течение 1 дня способен возрасти на 1 пункт с вероятностью 50 %, опуститься - 30 % и не измениться – 20 %. Какова вероятность поднятия курса на 2 пункта за 5 дней.
Решение. При рассмотрении условий задачи видно, что имеют место лишь 2 возможных варианта развития событий:
в первом случае курс может расти на протяжении двух дней, не падая и не меняясь в течение трех дней;
во втором случае – рост замечается на протяжении 3 дней, падение – 1 день, а также курс остается без изменений – 1 день.
Следовательно, можно составить выражение:
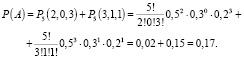
На основании проведенных расчетов видно – вероятность того, что за 5 дней торгов курс поднимется на 2 пункта составила 0,17.
При помощи теории вероятностей можно произвести расчеты на нахождение возможной прибыли, которую может получить страховая компания. Однако для этого необходимо знать количество потенциальных клиентов, условия страхового договора и вероятность наступления случаев, прописанных в нем. Следующий пример этим условиям соответствует, и мы можем произвести нужные нам расчеты [8].
Пример 3.
Страховая компания M обладает 100000 потенциальных клиентов. Для того, чтобы заключить договор личного страхования, необходимо заплатить 700 рублей. При наступлении страховых случаев, прописанных в договоре, имеющих вероятность p = 0,005, компания обязуется выплатить 55000 рублей. Какую прибыль может получить компания с надежностью 90 %?
Решение задачи необходимо начинать с определения формулы нахождения прибыли страховой компании. Для этого необходимо из общей суммы, которую внесут клиенты, вычесть ту сумму, которая будет выплачена страховой компанией ввиду становления случаев, указанных в страховом договоре.
Таким образом:
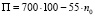тыс. руб.
Чтобы найти n0, необходимо воспользоваться формулой Муавра-Лапласа:
,
,
.
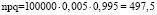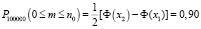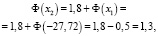
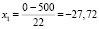Переоценить значение рассматриваемой науки достаточно трудно. С помощью теории вероятностей решают вопросы, связанные с изучением спорных и незаметных взаимосвязей разнообразных событий и явлений в разных отраслях науки. Теория вероятностей дает возможность точно определить колебания таких экономических показателей, как спрос, предложение, цены. Кроме того, теория вероятностей является основой такой науки, как статистика.
Рассматривая сферы применения теории вероятностей, трудно пройти мимо экономических и технических наук. На сегодняшний день сложно вообразить изучение явлений экономического и технического характера отбрасывая моделирование, которое опирается на использование теории вероятностей [9].
События, происходящие на автомобильных дорогах, уровень безопасности самого автотранспортного средства, автокатастрофы, разнообразные ситуации в процессе проектирования автомагистралей попадают в круг вопросов, решаемых с помощью способов теории вероятностей [10].
Проведенные исследования позволяют сделать вывод о важности практического применения методов теории. На основе решения задач в таких экономических сферах, как кредитование и страхование, мы наглядно увидели, что с помощью представленных методов можно производить расчеты, значимые для фирмы при планировании и прогнозировании, а также необходимые для увеличения эффективности экономики.