science-review.ru
Наблюдение за движением пузырька воздуха, выдуваемого из трубки расположенной у дна немагнитной цилиндрической колбы, заполненной магнитной жидкостью, поверх которой залита прозрачная немагнитная среда, проводилось по схеме, представленной на рис. 1 [1].
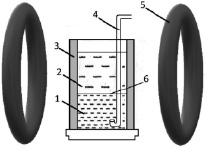
Рис. 1. Схема экспериментальной установки: 1 – магнитная жидкость, 2 – немагнитная прозрачная жидкость, 3 – стеклянный цилиндрический контейнер, 4 – пластиковая трубка, 5 – катушки Гельмгольца, 6 – граница раздела магнитной и немагнитной жидкости
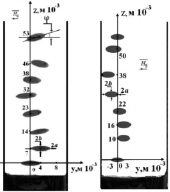
Рис. 2. Этапы движения пузырьков газа, окаймлённый магнитной жидкостью: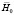 
– направление внешнего магнитного поля; а и b – полуоси эллиптического пузырька
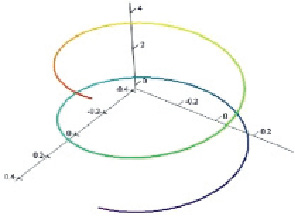
Рис. 3. Винтовая траектория движения пузырька. На осях отложены размеры в м?10-2
В магнитной жидкости 1, покрытой прозрачной немагнитной жидкостью 2, залитый в стеклянный контейнер 3, через трубки 4, выдувался пузырь газа. Вне стеклянного цилиндра, с помощью катушек Гельмгольца 5, создавалось магнитное поле. Пузырек, образованный на дне цилиндра, всплывал и пересекал границу раздела 6 магнитная – немагнитная среда. При пересечении границы он захватывал малый объем магнитной жидкости.
Пузырек, покрытый магнитной жидкостью, двигался вверх по винтовой линии. Всплытие пузырька, при включенном магнитном поле катушек Гельмгольца, регистрировались цифровой видеокамерой. Результаты этого наблюдения представлены на рис. 2.
С помощью этих рисунков изучалось движение пузырьков разной формы и размеров. Форма и размеры пузырька изменялись величиной приложенного магнитного поля [2].
В вертикальном направлении этих рисунков отложены вертикальные координаты движения пузырька, вдоль горизонтальной оси отложены горизонтальные перемещения пузырька при всплытии.
Траектория всплытия пузырька была описана с помощью математического пакета MathCad и представлена на рис. 3.
Колебание угла φ показанного на рис. 2, а, характеризующего поворот большой полуоси пузырька эллиптической формы относительно горизонта происходило по закону, графически представленному на рис. 4. Как следует из представленных на рис. 2, а, б траекторий движения пузырька, это движение представляет собой гармоническое колебание. Траекторию движения пузырька при всплытии подвергали анализу Фурье. То есть находили набор гармоник в спектре этого периодического процесса. Найденный спектр имеет вид представленный на рис. 4.
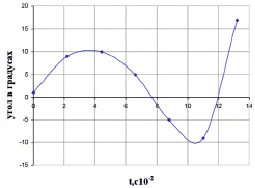
Рис. 4. Зависимость изменения угла φ отклонения большой полуоси (рис. 2, а) пузырька от горизонтальной оси от времени
Многочлен Фурье, характеризующий изменения угла φ при движении пузырька на рис. 2, а имеет вид:
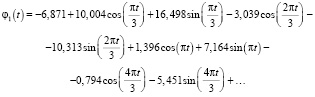
Объем пузырька в прозрачной жидкости менялся по закону приведенному на рис. 5. А пульсирующая форма пузырька мало отличалась от формы эллипсоида вращения с большой полуосью, направленной вдоль вектора внешнего магнитного поля, мог быть представлен в виде многочлена Фурье следующим образом:
а) для пузырька на рис. 2, а
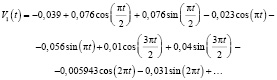
б) для пузырька на рис. 2, б
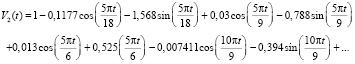
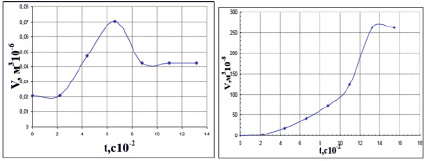
Рис. 5. График зависимости объема пузырька от времени: а) колебания объема пузырька рис. 2, а; б) колебание объема пузырька рис. 2, б
Описанный характер движения пузырька, объяснялся законами гидродинамики немагнитной жидкости омывающей пузырек. Магнитная жидкость, переносимая пузырьками, накапливалась на поверхности прозрачного слоя жидкости. И при достижении большого веса начинает каплями опускаться вниз. Падение капель представлено на рис. 6.
Рис. 6. Кинограмма падения капли магнитной жидкости
Первую половину пути капля движется равномерно и прямолинейно. Заметно лишь колебания объема капли. Вторую половину пути капля проходит по спирали со значительными колебаниями объема. Осуществлялся Фурье-анализ этих колебаний. Результаты разложения колебаний, падающих капель в ряды Фурье представлены графически на рис. 7, а, б, где ω – частота колебания, A – амплитуда колебания.
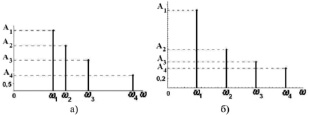
Рис. 7. Спектры колебаний, представленных па рис. 5, а и б, соответственно
Параметрические колебания капли магнитной жидкости, отрывающейся от горизонтальной поверхности в переменном магнитном поле [3].
Предыдущее наблюдение и анализ имели целью моделировать экспериментально и теоретически явления образования, роста и всплытия пузырьков пара при различных режимах парооброзования магнитной жидкости. Для той же цели мы приведены результаты наблюдения роста и отрыва капли магнитной жидкости от горизонтальной поверхности, выполненной из немагнитного материала в зависимости от внешнего постоянного и переменного магнитного поля. Использовался оптический метод регистрации профиля капли на различных стадиях процесса ее роста.
Истечение магнитной жидкости из отверстия на неограниченную поверхность немагнитного контейнера происходило под действием силы тяжести. Получены зависимости объема отрывающейся капли магнитной жидкости от величины приложенного поля. В постоянном горизонтальном поле при напряженности 6,8 кА/м для магнитной жидкости с намагниченностью насыщения 50,9 кА/м наблюдалось увеличение объема оторвавшейся капли в 6 раз. В постоянном вертикальном поле объем отрывающейся капли уменьшался почти в 2 раза. Изменение объема наблюдалось и на двух других концентрациях магнитной жидкости (40,1 кА/м и 32,3 кА/м). Изменение объема капли при отрыве в магнитном поле объясняется изменением параметра смачивания основанием капли поверхности подвеса, за счет этого изменяется величина капиллярных сил, удерживающих каплю [4].
Рис. 8. Возникновение неустойчивости на поверхности капли при напряженности магнитного поля 9,5 кА/м при различных значениях времени
На рис. 8 представлена киногорамма капли, растущей и отрывающейся в горизонтальном переменном магнитном поле при напряженности магнитного поля 9,5 кА/м. Под каждым снимком приведено время регистрации данной формы капли, начиная от момента истечения капли. Из рисунка, видно, что при определенном, достаточно малом, объеме капли на ее поверхности не возникает явления неустойчивости. При достижении каплей определенного объема на поверхности капли начинается бежать волна, наблюдаемая в дальнейшем вплоть до отрыва капли. На момент отрыва капли (рис. 8, д) ее столбик получается ступенчатым с примерно одинаковой длиной ступени, а нижняя часть капли утрачивает осесимметричную форму, удлиняясь в направлении внешнего приложенного магнитного поля [5].
Экспериментальное наблюдение за поведением пузырьков газа, всплывающих в двухслойной среде магнитная – немагнитная жидкость показали, что траектория всплытия этих пузырьков, при обеспеченных в экспериментах условиях, это движение по спирали с колебаниями горизонтальных осей пузырьков в вертикальной плоскости. Найдены спектры этих колебаний.
Наблюдение за истечением капли магнитной жидкости в переменном магнитном поле промышленной частоты показали, что при определенном объёме растущей капли, на ее поверхности образуется бегущая волна.
Работа выполнена при финансовой поддержки РФФИ (проект № 17-01-00037).