science-review.ru
В настоящее время для создания экономически развитого общества, активного продвижения научно-технического прогресса особая роль отводится математике. Математические методы сегодня находят широкое применение в различных областях естествознания, и в частности в экономике, поскольку все экономические категории и явления имеют количественную основу. Математический аппарат удобен для построения, анализа и дальнейшего изучения моделей экономических процессов и явлений, что дает возможность строить прогнозы и анализировать рыночную ситуацию. Таким образом, изучение количественных соотношений переходит в исследования качественного содержания наблюдаемых явлений и процессов, и наоборот.
При построении математической модели возможны два подхода: индуктивный – от более простой модели к общей модели всего процесса, и дедуктивный – от общей модели к более конкретной. Примером такого подхода может служить известное произведение «Капитал» К. Маркса. Сначала он вводит понятие относительной стоимости, сопоставляя стоимости разнородных товаров, а затем строит математические модели простого и расширенного воспроизводства и, наконец, приводит математическую модель нормы прибыли, произведя при этом ее математический анализ.
Математические модели экономических процессов и явлений (экономико-математические модели) можно классифицировать по разному основанию. Например, по целевому назначению: теоретико-аналитические и прикладные. Первые из них используются в исследованиях общих свойств и закономерностей экономических процессов. Другие применяются в решении конкретных экономических задач. В дальнейшем мы будем рассматривать прикладные модели, которые имеют дело с исключительно идеализированными экономическими объектами и ситуациями. Главным принципом построения таких моделей является получение аналитических результатов посредством математических доказательств и исследований. Модели экономических процессов чрезвычайно разнообразны по форме математических зависимостей. Особую роль в исследовании и построении математических моделей экономических процессов играют основные понятия и характеристики классического математического анализа. Применение теории функций, пределов, определенного и неопределённого интегралов позволяет более глубоко определить сущность экономических процессов, раскрыть новые соотношения между экономическими явлениями, влиять на ход и результаты теоретических исследований. Теория математического анализа моделей экономики в последствии реорганизовалась в отдельную дисциплину под названием математическая экономика.
Анализируя литературные источники по математической экономике, можно сделать вывод, что большинство авторов используют следующее определение экономико-математической модели [1, 2]: экономико-математическая модель – это математическое описание экономического объекта или процесса с целью их исследования и управления ими, это математическая запись решаемой экономической задачи. В учебном пособии [3, с. 6] под моделью понимается материальный или мысленно представляемый объект, который в процессе исследования замешает объект-оригинал так, что его непосредственное изучение лает новые знания об объекте-оригинале. Моделирование в экономике – это воспроизведение экономических объектов и процессов в ограниченных, малых, экспериментальных формах, в искусственно созданных условиях.
В экономике чаше используется математическое моделирование посредством описания экономических процессов математическими зависимостями. Объектом моделирования может быть либо реальная хозяйственная система, либо один или несколько процессов, протекающих в ней. Наиболее часто в экономике фигурирует понятие функции, так как функциональная зависимость позволяет получить наглядное представление изучаемого процесса или явления. В качестве примера рассмотрим линейную паутинную модель рынка, в которой спрос d(p) и предложение s(p) являются линейными функциями цены р. Общие положения теории по паутинной модели рынка можно найти в [4]. Мы лишь остановимся на рассмотрении конкретного примера с подробными пояснениями к нему.
Пример 1. В паутинной модели рынка даны функция спроса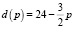 
, функция предложения s(p) = 3p – 3 и начальная цена p0 = 5. Построить графики этих функций, найти координаты точки рыночного равновесия и несколько узлов ломаной 
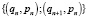. Получить общую формулу для 
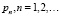. Найти 
.
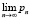Решение.
Найдем точку рыночного равновесия р*. Для этого приравниваем d(p) и s(p):
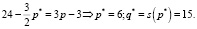
Находим начальное количество товара из функции спроса:
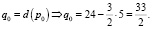
Находим текущую цену pn. Она определяется текущим спросом qn:
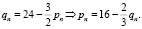
Количество товара qn+1, которое будет выпущено в следующем году, определяется функцией предложения, зависящей от текущей цены: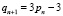 
.
Последовательно находим точки ломаной: q1 = 12, p1 = 8, q2 = 21, p2 = 2, q3 = 3, p3 = 14 и так далее. Результаты расчетов изобразим графически на плоскости (p; q). Для этого выпишем первые точки ломаной: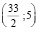 
, (12; 5), (12; 8), (21; 8), (21; 2), (3; 2), (3; 14). Следует отметить, что точки (qn, pn) лежат на графике спроса d(p), а точки (qn+1, pn) лежат на графике функции предложений s(p). Особое внимание надо обратить на то, что аргумент р откладывают по оси ординат, а функцию q – по оси абсцисс. Последовательно находим точки ломаной: q1 = 12, p1 = 8, q2 = 21, p2 = 2, q3 = 3, p3 = 14 и так далее. Результаты расчетов изобразим графически на плоскости (p; q).
Для этого выпишем первые точки ломаной: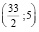 
, (12; 5), (12; 8), (21; 8), (21; 2), (3; 2), (3; 14). Следует отметить, что точки (qn, pn) лежат на графике спроса d(p), а точки (qn+1, pn) лежат на графике функции предложений s(p). Особое внимание надо обратить на то, что аргумент р откладывают по оси ординат, а функцию q – по оси абсцисс.
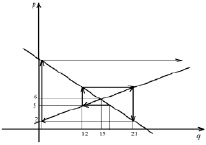
В результате получили паутинную модель рынка, в которой функции спроса и предложения имеют линейную зависимость с ценой р.
Найдем теперь общую формулу для pn, воспользовавшись равенством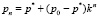 
. Здесь k равен отношению коэффициентов при аргументе р, в нашем случае 
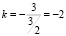. Следовательно, 
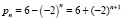и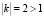 
, поэтому последовательность {pn} является бесконечно большой. На рисунке этот факт отражен направлением стрелок в паутинной диаграмме.
Рассмотрим приложения производной в экономической теории. Математической основой такого приложения является теорема Ферма, которая утверждает: если дифференцируемая на некотором промежутке функция достигает наибольшего ил наименьшего значения во внутренней точке этого промежутка, то производная функции в этой точке равна нулю. Экономической интерпретацией теоремы Ферма является базовый закон теории производства, который утверждает, что оптимальный для производителя уровень выпуска товара определяется равенством предельных издержек и предельного дохода. Отсюда следует, что уровень выпуска x0 является оптимальным, если MS(x0) = MD(x0), где MS – предельные издержки, MD – предельный доход.
Обозначим функцию прибыли C(x). Тогда C(x) = D(x) – S(x), где D(x) – функция дохода, а S(x) – функция издержек. Очевидно, что оптимальным уровнем производства является тот, при котором прибыль максимальна, т.е. такое значение x0, при котором функция C(x) имеет экстремум (максимум).
Пример 2. Найти максимальную прибыль, которую может получить производитель при условии, что весь товар реализуется по фиксированной цене р = 10,5 (ден. ед.) за единицу товара, а функция издержек имеет вид
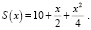
Решение.
Найдем функцию прибыли
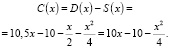
Исследуем эту функцию на экстремум. Для этого найдем производную этой функции:
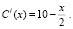
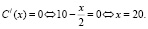
Так как х это количество товара, то x > 0, поэтому исследуем производную C/(x) на промежутке (0; +∞). Так как при переходе через точку x = 20 производная меняет знак с плюса на минус, то x = 20 – точка максимума функции C(x).
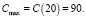Поэтому максимальная прибыль производителя составит 90 денежных единиц.
Уровень наиболее экономичного производства определяется равенством средних и предельных издержек. Напомним, что средние издержки AS(x) это издержки по производству товара, делённые на произведённое его количество. Минимум этой величины достигается в критической точке функции y = AS(x). Рассмотрим более подробнее задачу, которая приведена в [5].
Пример 3. На начальном этапе производства фирма минимизирует средние издержки. В дальнейшем цена единицы товара устанавливается в размере p = 537 (ден. ед.). Какое оптимальное количество товара должна производить фирма, если функция издержек имеет вид: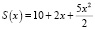 
?
Решение.
Средние издержки равны отношению функции издержек произведённого товара к его количеству, т.е.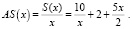 
Найдём при каком значении х они принимают минимальное значение:
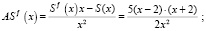
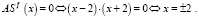
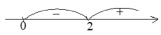
Производная меняет знак с минуса на плюс. Следовательно, xmin = 2.
Предельные издержки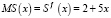 
. При p = 537 оптимальное значение выпуска задаётся условием 
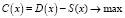. Так как 
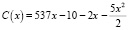, то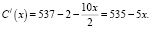 
Следовательно, 
.
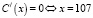Значит оптимальное количество выпускаемой продукции xопт. = 107.
Приведем теперь пример приложения дифференциального исчисления функции нескольких (и в частности двух) переменных в экономике. К наиболее часто встречающимся таким функциям относятся функция полезности и производственная функция. При решении задач с указанными функциями используется теоремы, устанавливающие необходимые и достаточные условия существования экстремума, а в случае наложения дополнительных условий задача сводится к исследованию функции одной переменной. Например, производственная функция, выражающая результат производственной деятельность от обусловивших его факторов, наиболее часто встречается в виде функции Кобба-Дугласа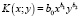 
.
Важнейшим направлением применения дифференциального исчисления в экономике является введение с его помощью понятия эластичности. Коэффициент эластичности показывает относительное изменение исследуемого экономического показателя под действием единичного относительно изменения экономического фактора, от которого он зависит.
Пример 4. Заданы производственная функция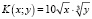 
и цены p1 = 2 и p2 = 4 за единицу первого и второго ресурсов соответственно, а так же ограничения не более 500 ден. ед. в сумме, которая может быть потрачена на приобретение ресурсов. Найти величины х и у, при которых фирма получит наибольшую прибыль.
Решение.
Так как в задаче речь идет о двух видах ресурсов, то функция издержек будет иметь вид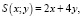 
а получаемая прибыль
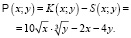
Максимизируем функцию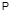 
(x; y) при условии 2x + 4y = 500. С учетом имеющегося ограничения x = 250 – 2y и функция прибыли запишется в виде
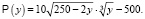
Тогда
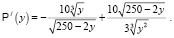
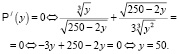
В этом случае x = 150. Таким образом, наибольшая прибыль будет получена при x = 150, а y = 50.
Из приведенных примеров можно сделать вывод о том, что уже при решении задач, в которых использовались только основные положения теории функций и экономический смысл производной, можно сделать вывод о том, что модели экономических процессов чрезвычайно разнообразны по форме математических зависимостей. Особенно следует выделить класс линейных моделей, наиболее удобных для анализа, вычислений и наглядной интерпретации, вследствие чего они получили наибольшее распространение (например, линейная модель рынка). Однако, различие между линейными и нелинейными моделями существенны не только с математической точки зрения, но и в теоретико-экономическом отношении, поскольку многие зависимости в экономике носят принципиально нелинейный характер: эффективность использования ресурсов при увеличении производства, изменение спроса и потребления населения при увеличении производства и т.д. Часть таких зависимостей рассмотрена в примерах 2–4.