С начала 21 века произошел большой скачок в развитии образовательного процесса с точки зрения инноваций. Все началось с компьютеризации школ и теперь во всех школах есть минимальный набор информационных технологий, которые внесли улучшения в процесс обучения, с одной стороны, и ухудшения – с другой.
Так что же это за улучшения и ухудшения? Говоря о первом, можно сказать, что информационные технологии, безусловно, улучшили процесс обучения. Компьютеры облегчили подготовку к урокам, особенно геометрии. Если раньше все конспекты уроков учитель готовил самостоятельно, измеряя до миллиметра каждый чертеж и готовя карточки с заданиями своими руками, убивая огромное количество времени, то компьютер это делает быстрее и качественней, ведь существуют специальные программы, которые позволят построить любой чертеж или модель, по заданным координатам. Тот же урок становится более наглядным, если вы используете презентации.
Ученые доказали, что учащиеся сохраняют 20 % того, что они слышат, 30 % того, что видят и 50 % того, что они видят и слышат. Таким образом, мы можем заключить, что наглядность играет важную роль. Если говорить о геометрии, то обучающимся трудно даётся обучение этому предмету. По 6 класс, школьный курс состоит из математики, а в 7 классе происходит разделение математики на геометрию и алгебру, а последняя дается им лучше, чем геометрия. Это объясняется тем, что алгебра ближе к математике, а геометрических задач было значительно меньше. Поэтому возникает острая проблема изучения геометрического материала и тут на помощь приходят информационные технологии. С помощью наглядности материал становится доступным для изучения. Также, если изучать учебные пособия, прилагаемые к УМК по геометрии, то процесс обучения, согласно современным стандартам, предполагает много самостоятельной работы для учеников с использованием информационных технологий. Это подготовка докладов, презентаций, биографии и прочее. Так учащиеся чувствуют себя частью учебного процесса и развивают интерес к предмету и закрепляют навыки работы на компьютере [1, 2].
Все бы хорошо, если бы не одно «НО», которое омрачает идею компьютеризации в учебном процессе. Это те недостатки, которые заставляют задуматься о том, действительно ли информационные технологии помогают, а не вредят? Особого негативного влияния на организм человека компьютером, специалисты пока не доказали, но любая техника-это прежде всего радиация. Таким образом, если учащиеся имеют дело с компьютером, интерактивной доской или чем-то еще, связанным с информационными технологиями в каждом классе, то нагрузка на организм ребенка и его отдельные органы, например зрение, будет сказываться негативным образом.
Также все мы знаем, что интернет и гаджеты, с которыми люди имеют дело, вызывают некоторую зависимость. Особенно остро эта проблема стоит в нашем веке новых технологий. Каждый ребенок, с его или ее не укрепленной психикой, подвержен зависимости от них. Поэтому если каждый день, большое количество времени, ученику приходится иметь дело с компьютером и интернетом, то со временем его образовательный интерес перерастет в своеобразную зависимость.
С внедрением информационных технологий процесс обучения стал немного проще, но также добавились и другие негативные аспекты этой реализации. Так что не забывайте о балансе. Чувство меры в этой ситуации играет огромную роль, и чтобы не навредить здоровью и психике ребенка, педагог должен четко разграничить грань между информационными технологиями и образовательным процессом.
Как мы уже говорили, геометрия-это сложная наука, изучающая свойства различных фигур на плоскости и в пространстве. Еще до нашей эры она помогала в сельском хозяйстве, откуда и возникла, а в переводе с древнегреческого означает «измерение земли».
Такой предмет, как геометрия занимает огромное место в развитии личности ребенка. Эта наука помогает развивать логическое мышление, пространственное воображение, зрение, память, творческие качества. Поэтому учителя с большой ответственностью должны подходить к своей работе, ведь от того, как преподнести предмет и материал, зависит успешное развитие у учащихся всех этих качеств. Особенно это касается геометрических построений.
Задачи на построение играют особую роль в геометрии. «Они являются важным средством формирования геометрических представлений учащихся в целом. В процессе геометрических построений учащиеся в практическом плане знакомятся со свойствами геометрических фигур и отношений, учатся пользоваться чертежными инструментами, приобретают графические навыки. В правильности многих математических утверждений в большинстве случаев школьники убеждаются также в процессе геометрических построений» [3].
Данную тему можно назвать актуальной. Она заключается в необходимости формирования методологических аспектов обучения геометрическим построениям на плоскости с использованием информационных технологий и приобщения подрастающего поколения к использованию инноваций в образовательных целях.
Цель исследования: необходимо научное обоснование и разработка методических подходов к обучению геометрическим построениям на плоскости и возможность использования в процессе обучения геометрии информационных технологий, с целью развития у учащихся интереса к предмету и познавательного интереса в целом.
Материалы и методы исследования
Если рассмотреть курс геометрии в школьных учебниках, то можно заметить что с геометрическими построениями ученик сталкивается в конце 5 класса, в конце 6 класса, в начале 7 класса. В 8 и 9 классе мы встречаем более углубленное изучение заданий на построения. Особенное место уделяется задачам на построение с применением чертежных инструментов, а именно – циркуль и линейка.
Такие задачи имеют следующую схему решения:
– Анализ: сформулируем решения, при различных методах построения;
– Построение: осуществляется план, составленный в результате анализа;
– Доказательство: доказывается, что решение удовлетворяет условию задачи;
– Исследование: рассматриваются всевозможные пути решения этой задачи.
Задачи на построение решаются различными способами. Рассмотрим некоторые из них:
1. Метод геометрических преобразований:
– Метод центральной симметрии. «В условии задачи в той или иной форме указана точка, являющаяся центром симметрии искомой или вспомогательной фигуры» [4].
– Метод осевой симметрии. «В условии задачи указана прямая, являющаяся осью симметрии части элементов фигуры» [4].
– Метод параллельного переноса. «При анализе задачи трудно найти зависимость между данными элементами, позволяющую построить искомую фигуру, но если мы какую-нибудь часть или всю фигуру перенесем параллельно в некотором направлении на определенное расстояние, то получим вспомогательную фигуру, которую легко можно построить» [4].
– Метод поворота. «Если в задаче, где либо части фигур сближаются в положение, удобное для построения, либо при заданных явно или косвенно центре и угле поворота требуется отыскать две соответственные точки, лежащие на данных или искомых фигурах» [4].
– Метод подобия. «Задача решается методом подобия, если ее условие можно разделить на две части, одна из которых определяет форму фигуры с точностью до подобия, а вторая – размеры фигуры» [4].
2. Метод геометрических мест точек. Имеет ли решение задача или нет в зависимости от того, будут или нет ГМТ, иметь общие точки. Она будет иметь столько решений, сколько имеется точек пересечения.
3. Алгебраический метод. «Составляют уравнение или систему уравнений по условию задачи; решают полученное уравнение или систему и находят нужное неизвестное; осуществляют геометрическое построение по полученной формуле» [4].
4. Метод инверсии. Проектирование от противного.
Результаты исследования и их обсуждение
Мы пришли к выводу, что основу геометрических построений на плоскости, составляют задачи на построение. Далее рассмотрим примеры задач на построение, несколькими методами и рассмотрим возможность использования информационных технологий.
I. Метод поворота. «Земельный участок квадратной формы был огорожен. От изгороди сохранились два столба на параллельных сторонах квадрата. Кроме того, остался столб в центре квадрата. Требуется восстановить границу участка» [3].
«Анализ. Пусть ABCD – искомый квадрат, О – его центр, М и N – данные точки соответственно на сторонах АВ и CD (рис. 1). Если повернуть квадрат на 180 ° около его центра О, то он преобразуется сам в себя. Точка Мзаймет некоторое положение М’ на стороне CD, а точка N – некоторое положение N’ на стороне АВ. После этого нетрудно уже построить прямые АВ и CD и восстановить искомый квадрат.
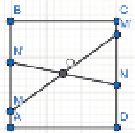
Рис. 1
Построение. 1) Строим точку М’, симметричную М относительно 0, и точку N’, симметричную N относительно О. 2) Строим прямые MN’ и NM’. 3) Повернем построенные прямые около точки О на 90 °. Четыре построенные прямые ограничивают искомый квадрат.
Доказательство опускаем.
Исследование. По смыслу задачи невозможен случай, когда точки М и N располагаются с точкой О на одной прямой, но не симметричны относительно О. Если точки М и N симметричны относительно О, то задача становится неопределенной. В остальных случаях задача имеет единственное решение» [4].
II. Метод геометрических мест точек. «Построить треугольник по основанию а, высоте ha и боковой стороне b.
Анализ. Предположим, что треугольник АВС построен и у него ВС = a, СА = b и высота, опущенная из вершины А, равна ha. Тогда множество всех вершин треугольников с данным основанием a и высотой ha будут лежать на двух прямых, параллельных ВС и отстоящих от нее на расстоянии ha.
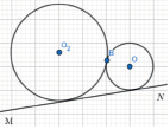
Рис. 2
Далее, т.к. СА = b, то точка А находится на данном расстоянии от точки С, а, значит, лежит на окружности радиуса b с центром в точке С. Значит, точка А является пересечением двух ГМТ и, следовательно, определяется.
Построение. На произвольной прямой MN от произвольной точки В откладываем отрезок ВС = a. Из любой точки К прямой MN проводим прямую FK ^ MN и на FK от K в обе стороны откладываем отрезки KT и KE равные ha . Через Т и Е проводим прямые n и m, перпендикулярные ТЕ. Из точки С проводим окружность радиуса b.
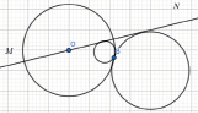
Рис. 3
Точка пересечения этой окружности с прямыми m и n является искомой точкой А. Соединяем ее с точками В и С. Треугольник АВС – искомый.
Доказательство. В треугольнике АВС основание ВС = a по построению, вершина А удалена от основания на расстояние ha , а боковая сторона АС = b.
Исследование. Если b > ha, то имеем четыре решения. Т.к. окружность радиуса a пересечет прямые m и n в четырех точках.
Если b = ha , то получаем два решения, т.к. прямые m и n будут касаться окружности.
Если b < ha , то решений нет» [4,5].
III. Алгебраический метод. «Даны отрезки а и b. Построить отрезок <<hatoh01.wmf>>
Решение. Строим прямой угол с вершиной О (рис. 4). На его сторонах откладываем отрезки ОА = a и ОВ = b. Тогда отрезок АВ является искомым» [4].
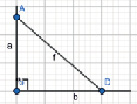
Рис. 4
Решение всех этих задач трудно представить без наглядности и логического мышления. С помощью интерактивной доски и компьютера можно рассмотреть условие задачи, создать модель и выполнить анализ. На обычной доске это не так наглядно и долго. Поэтому преподаватель должен уметь правильно преподнести материал, что бы сэкономить время на занятиях и заинтересовать ученика.
Обозначим основные направления использования информационных технологий:
– Материал для демонстраций: схемы, таблицы, упражнения и др.;
– Визуальная информация: наглядный, иллюстрированный материал;
– Тренажеры;
– Контроль умений и навыков обучающихся.
Информационные технологии помогают сделать процесс обучения проще, доступнее, интереснее [6].
Заключение
Информационные технологии являются эффективным средством повышения качества образовательного процесса. Основным способом изучения материала является интерес к нему. Если есть интерес, то ученику не составит труда разобраться в курсе геометрии.
На уроках геометрии использование ИКТ не только возможно, но и необходимо. Развитие личности ребенка остается главным критерием методики обучения геометрии, поэтому приветствуются всевозможные способы обучения, которые будут его интересовать и способствовать его развитию.
Не стоит забывать о зависимости школьников от компьютеров и интернета, поэтому необходимо знать меру в их использовании, а родителям контролировать время, проведенное за компьютером.


 science-review.ru
science-review.ru