Снижение уровня школьного математического образования, уменьшение аудиторных часов выделенных на преподавание предметов математического цикла в технических вузах влияет на качество математического образования и на формирование математической компетентности. Сергеева Е.В. считает, что интенсивное развитие современного производства со сложным техническим оснащением невозможно без сформированности математической компетентности [1]. В основу математической компетентности на большинстве направлений инженерных специальностей лежат такие компетенции как знания и умения применять законы естественнонаучных дисциплин в будущей профессиональной деятельности, умения математического моделирования в теоретических и экспериментальных исследованиях. Исследователи Л.Д. Кудрявцев, В.А. Садовничий, В.И. Тихомиров и др. в своих работах утверждают, что повышение качества университетского образования неразрывно связано с повышением качества математического образования.
Матвейкина В.П. считает, что согласно новая образовательная парадигма независимо от специализации и характера работы любой начинающий специалист должен обладать фундаментальными знаниями, профессиональными умениями и навыками деятельности своего профиля, опытом творческой и исследовательской деятельности по решению новых проблем, опытом социально оценочной деятельности [2].
Главным недостатком школьного математического образования является неполное понимание школьниками смысла некоторых операций. Например, на вопрос «что такой производная?» каждый год получаем один и тот же ответ – «штрих», несмотря на то, что в ЕГЭ есть задания на геометрический и физический смыслы производной. Большинство старшеклассников нацелены на решение только алгоритмизированных задач, что приводит к неумению решать нестандартные задачи и интегрировать знания из различных областей наук для решения нестандартных задач в будущей профессиональной деятельности.
Цель исследования – формирование у студентов первокурсников понятия производной функции одной переменной; формирование умения описывать математическую модель задачи; формирование умения применять производные в различных областях наук при проведении исследований и при изучении спец. дисциплин.
Методы исследования:
– интеграция – на предметах математического цикла рассматривали различные задачи из разделов физики, экономики и математики в которых студенты учились описывать математические модели задач и решать их через дифференцирование;
– практический метод прикладного анализа – на конкретных задачах показывали применение производных аналитически и геометрически.
На первом этапе при формировании у студентов понятия производной на математике мы вводим понятие механического смысла производной как скорости изменения какого-либо процесса, рассматривая широкий спектр моделей скоростей протекания различных процессов ранее изученных по физике в школе (таблица).
Модели изменения скорости физического процесса
|
Функция, описывающая процесс |
Скорость изменения процесса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Геометрический смысл производную функции y=f(x) можно трактовать как скорость изменения функции: чем больше 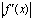 , тем больше угол наклона касательной к кривой, тем круче график f(x) и быстрее растёт (убывает) функция.
, тем больше угол наклона касательной к кривой, тем круче график f(x) и быстрее растёт (убывает) функция.
Студенты на первом курсе впервые сталкиваются с задачами, где надо найти производную функция заданной геометрически или в виде таблицы. Из-за дефицита времени на проведение аудиторных часов по предметам математического цикла не на всех направлениях преподаватели имеют возможность ознакомить на первом курсе методом наименьших квадратов, поэтому и возникает необходимость графического и численного дифференцирования.
Графическое дифференцирование – метод касательных основанный на геометрической интерпретации производной. Проведение на глаз касательной является неточной. Для уточнения используют прибор – зеркальный дериватор, служащий для проведения нормали к линии (в качестве простейшего зеркального дериватора используют зеркала прямоугольной формы) [3].
Численное дифференцирование – приближенное вычисление производных для таблично заданной функции [4]. Численное дифференцирование можно использовать и для вычисления производной аналитически заданной функции, когда производная имеет слишком сложное для вычислений выражение.
Умение применять производную при решении задач, при проведении исследований требует знания и понимание теоретического материала, а также понимания о её необходимости в инженерной деятельности. С целью формирования понимания необходимости использования производной в будущей профессиональной деятельности студентам было задано домашнее задание найти примеры использования производной в различных областях наук являющиеся фундаментальными для инженерного образования: в физике скорость, ускорение, сила тока, теплоемкость, линейная плотность, коэффициент линейного расширения, угловая скорость, угловое ускорение; в экономике предельные показатели в экономике, эластичность экономических показателей, рост производительности труда; в химии скорость химической реакции в данный момент времени.
Для закрепления выдается домашняя контрольная работа для каждого студента индивидуально. Часть А – повторение школьного курса. Часть В – задания где необходимо уметь брать производные от функции заданной параметрически, неявно и от показательно-степенных функций, использовать правило Лопиталя при решении пределов, находить кривизну или координаты центра кривизны линии, используя численные методы найти производную от функции заданной таблично. Часть С – прикладная часть, где используется умение составлять математическую модель и находить производную (задания 1 и 2 для студентов обучающихся на инженерных специальностях, задания 3 и 4 для студентов экономического профиля).
Образец варианта индивидуальной контрольной работы по математике «Дифференциальное исчисление функции одной переменной»
Часть А.
1. Найти производные первого порядка данных функций:
1) 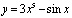 ; 2)
; 2) 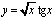 ;
;
3) 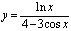 ; 4)
; 4) 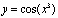 .
.
2. Провести полное исследование функции и построить ее график:
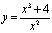 .
.
3. Найти производную 3-го порядка данной функции: 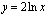 .
.
4. Найти наибольшее и наименьшее значения функции 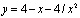 на отрезке [1, 4].
на отрезке [1, 4].
5. Составить уравнения касательной и нормали к графику функции 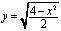 в точке
в точке 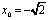 .
.
Часть В.
1. Найти производные первого порядка данных функций:
1) 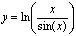 ;
;
2) 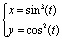 ;
;
3) 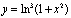 ;
;
4) 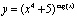 .
.
2. Вычислить пределы используя правило Лопиталя:
1) 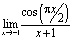 ;
;
2) 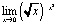 .
.
3. Вычислить координаты центра кривизны кривой 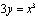 в точке (–1; –1/3).
в точке (–1; –1/3).
4. Пример. Вычислить первую и вторую производные от таблично заданной функции
yi = f(xi) = 0, 1, 2, 3, 4, в точке х = X*;
X* = 0.2.
|
i |
0 |
1 |
2 |
3 |
4 |
|
xi yi |
0.0 1.0 |
0.1 1.1052 |
0.2 1.2214 |
0.3 1.3499 |
0.4 1.4918 |
Часть С.
Плот подтягивается к берегу при помощи каната, который наматывается на ворот со скоростью 3 м/мин. Определить скорость движения плота в тот момент, когда его расстояние от берега будет равно 25 м, если ворот расположен на берегу выше поверхности воды на 4 м.
Тело массой 6 г движется прямолинейно по закону
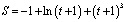
(S выражено в сантиметрах, t – в секундах). Требуется вычислить кинетическую энергию 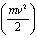 через 1 секунду после начала движения.
через 1 секунду после начала движения.
Зависимость издержек производства от объёма выпускаемой продукции выражается формулой 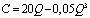 денежных единиц. Определить средние и предельные издержки при объёме продукции стоимостью Q=10 ден. ед [5] .
денежных единиц. Определить средние и предельные издержки при объёме продукции стоимостью Q=10 ден. ед [5] .
Спрос на товар определяется формулой 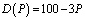 . Найти эластичность спроса при цене на товар P=20 ден. ед [5].
. Найти эластичность спроса при цене на товар P=20 ден. ед [5].
На первом курсе студенты на занятиях по физике сталкиваются с необходимостью дифференциального и интегрального исчисления. Студенты в основном опираются на школьные представления о понятии производной, поскольку изучение данной темы на большинстве направлений на математике начинается позже. В вузе записываются по-новому физические величины и законы. Слабая подготовка абитуриентов по физике и математике приводит к тому, что сложные физические задачи с нахождением производной становятся не доступными для понимания.
В рамках профориентационной работы усилиями преподавателей физики и математики в ВПИ проводятся различные мероприятия с целью повышения качества физико-математического образования школьников:
– на подготовительных курсах преподаватели проводят занятия, не только ориентируясь на ЕГЭ, но и проводят взаимосвязь между курсом средней школы и базовым физико-математическими понятиями, с которыми столкнутся при обучении в техническом вузе;
– в рамках ежегодной комплексной олимпиады «Роботландия» задания по физике и математике подбираются таким образом, что абитуриент поэтапно обучается навыкам самостоятельной исследовательской деятельности (применение производной в физике, построение и чтение графиков при применении физических законов, решение качественных задач). Используя несложный математический аппарат, можно составить интересные задания с целью адаптации школьного курса с вузовским.
– в рамках проекта «70+» проводится тематические практические занятия по решению сложного уровня задач из 2 части ЕГЭ (физика). Данный курс предназначен для подготовленных абитуриентов, разбирая экзаменационные задания, преподаватель также знакомит с новыми вузовскими приемами решения задачи.
Без понятия производной функции не обходится, пожалуй, ни одна из тем по физике, поскольку многие физические величины изменяются со временем. Методика введения понятия производной начинается уже на первых лекционных занятиях с таких понятий как скорость, ускорение, угловая скорость и угловое ускорение (таблица).
Образец варианта индивидуальной контрольной работы по физике по теме «Кинематика»
Уровень А.
1. Движение некоторого тела задано уравнением x=3t+4t3.Для моментов времени t1=0 и t2=4c найдите скорость, ускорение, а также средние значения скорости и ускорения за первые 4 c движения?
2. Для точек находящиеся на карусели на расстоянии R=2 м от оси вращения определите угловую скорость, и угловое ускорение для момента времени 2 с. Карусель вращается согласно закону j =t+2t3.
3. Продолжите фразу. Величина, характеризующая в данный момент времени быстроту и направление движения точки…..
а) ускорение; б) скорость; в) сила; г) угловое ускорение.
Уровень B.
Два бильярдных мяча движутся вдоль прямой Оx, согласно законам:
x1 = 4t + 4t2 – 3t3 и x2 = 2t – 2t2 + t3.
Найдите момент времени, при котором их ускорения будут совпадать.
Некоторый груз на нити длиной 2 м вращают вокруг вертикальной оси при этом нормальное ускорение задается уравнением an = 1 + 6t + 9t2. Для момента времени 5 с оцените: тангенциальное ускорение и полное ускорение.
На графике представлено изменение проекции угловой скорости со временем вращающегося диска. Постройте график изменения проекции углового ускорения со временем.
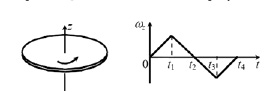
Уровень С.
1. Камень движется, таким образом, что радиус-вектор изменяется со временем по закону r = t3i + 3t2j, где i, j – орты осей х и у. Найдите скорость, и ускорения камня в момент времени t = 2 с, а также максимальную скорость камня.
2. Колесо автомобиля R = 40 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = 2 + 6t3. . Определить для точек на ободе колеса: нормальное ускорение an в момент времени t = 2 с; тангенсальное ускорение для этого же момента времени; угол поворота φ, при котором полное ускорение составляет с радиусом колеса угол α = 60°
Критерии оценки контрольных работ по физике и математике:
– «удовлетворительно»: решение заданий на уровне узнавания и воспроизведение по алгоритму, решено правильно от 60 % до 75 % заданий;
– «хорошо»: преобразовывает алгоритмы с условиями отличающимися от стандартных, решено правильно от 76 % до 89 % заданий;
– «отлично»: решены нестандартные задания с элементами исследования, правильно выполнены чертежи, решено правильно от 90 % до 100 % заданий.
Результаты проведённого исследования показывают высокую эффективность применения методов интеграции и прикладного анализа при изучении темы дифференцирование функции одной переменной и позволяют утверждать, что у студентов формируется устойчивое понимание производной, а также формируются навыки выбора необходимого математического инструментария при решении задач по физике и задач в будущей профессиональной деятельности.
Выводы:
– студент будет заинтересован в формировании математической компетентности, если он будет чётко понимать о необходимости полученных знаний в будущей профессиональной деятельности;
– данный подход в преподавании темы позволяет студентам эффективно усвоить материал, самостоятельно находить пути решения задач и строить дальнейший образовательный маршрут;
– решать проблему дефицита аудиторных часов переводя студентов на самостоятельное изучение лекционного материала, часто приводит к неправильному пониманию материала и большим временным затратам студента;
– экономить время можно за счёт подготовки заранее преподавателем рабочих тетрадей по практическому курсу, методических указаний с подробными комментариями.


 science-review.ru
science-review.ru
 – изменение скорости неравномерного движения в зависимости от времени t
– изменение скорости неравномерного движения в зависимости от времени t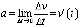 – мгновенное ускорение
– мгновенное ускорение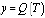 – изменение количества теплоты, сообщаемой телу при нагревании его до температуры T
– изменение количества теплоты, сообщаемой телу при нагревании его до температуры T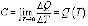 – теплоёмкость тела.
– теплоёмкость тела.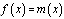 – масса стержня
– масса стержня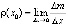 – линейная плотность неоднородного тонкого стержня в точке х0.
– линейная плотность неоднородного тонкого стержня в точке х0.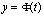 – изменение магнитного потока в зависимости от времени t
– изменение магнитного потока в зависимости от времени t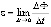 – мгновенное значение электродвижущей силы индукции
– мгновенное значение электродвижущей силы индукции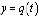 – изменение заряда в колебательном контуре в зависимости от времени t.
– изменение заряда в колебательном контуре в зависимости от времени t.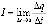 – сила тока I в контуре в момент времени t0
– сила тока I в контуре в момент времени t0