Scientific journal

Научное обозрение. Педагогические науки

ISSN 2500-3402

ПИ №ФС77-57475

Эконометрические модели широко применяются во всех сферах жизни. Особенно большое значение эконометрическая наука имеет в экономике и финансах. Интересно использование эконометрических моделей в банковском деле. Любой банк должен понимать, за счет чего можно достичь высоких показателей деятельности, должен прогнозировать свои будущие доходы. Эконометрика является важным инструментом, который может помочь руководству банка определить дальнейшее развитие и стратегию банка.

Рассмотрим построение эконометрической модели на примере конкретного банка – «Ак Барс». ПАО АКБ «Ак Барс» – крупный универсальный банк с государственным участием. Основные направления деятельности – кредитование и расчетно-кассовое обслуживание корпоративных клиентов, в том числе предприятий, находящихся в собственности государства, а также операции с ценными бумагами и привлечение средств населения во вклады [1]. Согласно кредитному рейтингу Moody’s Investors Service имеет оценку В2 (позитивный). Среди российских банков находится на 15 месте по объему собственного капитала, а также на 23 месте по объему активов [2]. «Ак Барс» – лучший региональный банк России (согласно Frank Research Group в 2017 г.).

Целью настоящей работы является составление эконометрической модели чистых доходов «Ак Барс» Банка на основе показателей его деятельности. Автор работы определил следующие задачи, которые необходимо решить в ходе работы:

– подобрать спецификацию модели, найти оцененные значения параметров;

– проверить выполнение предпосылок теоремы Гаусса-Маркова;

– в случае невыполнения какой-либо из предпосылок – устранить ошибки и получить модель с выполнением всех предпосылок теоремы;

– проверить адекватность модели и оценить ее практическую пользу.

Для того чтобы составить спецификацию модели, необходимо проанализировать отчетность ПАО «Ак Барс» Банка. Для этого используем поквартальный отчет о финансовых результатах данного банка, находящийся в открытом доступе на сайте Центра раскрытия корпоративной информации (представлены отчеты с 01.01.2007, поэтому объем данных будет включать 46 наборов) [3]. Определим, что на чистый доход могут оказывать влияние следующие факторы: процентные доходы от размещения средств в кредитных организациях (КО); от ссуд, предоставленных клиентам, не являющихся кредитными организациями (КЛ); от вложений в ценные бумаги (ЦБ). Составим таблицу со соответствующими квартальными значениями регрессоров и результирующего показателя. Спецификация модели имеет следующий вид (1.1):

ЧДt = а0 + а1*КОt + а2*КЛt + а3*ЦБt + ut (1.1)

а0 > 0, а1 > 0, а2 > 0, а3 > 0.

Все коэффициенты должны быть больше нуля, поскольку все регрессоры имеют прямую связь с результирующим показателем (увеличивают его значение при прочих равных условиях). Условимся, что на протяжении всей работы мы будем проводить необходимые нам вычисления на 5 %-ном уровне значимости. Для получения оцененной модели (1.1) используем метод наименьших квадратов (МНК). Получаем следующую модель (1.2):

ЧДt = 2351779 + 0,540*КОt + 0,238*КЛt – 0,315*ЦБt + ut (1.2)

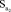= 732229; 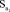= 0,716; 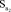= 0,073;

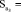0,340; σ = 2318198.

Мы получили, что коэффициент а3 < 0, чего быть не может. Более того, проверка на значимость данного фактора по критерию Стьюдента показала, что мы можем исключить показатель доходов от вложений в ценные бумаги:

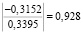< tкр (tкр = 2,018) => показатель ЦБ является незначимым.

Тогда оставим два регрессора – КО и КЛ – и получим новую спецификацию (2.1):

ЧДt = а0 + а1*КОt + а2*КЛt + ut (2.1)

а0 > 0, а1 > 0, а2 > 0.

Рассчитаем новую оцененную модель (2.2):

ЧДt = 2409427 + 0,134*КОt +

+ 0,189*КЛt + ut (2.2)

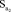= 723400; 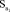= 0,564; 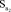= 0,048;

σ = 2357517.

Проверим модель на наличие типовых ошибок эконометрических моделей. Проверим модель на включение в нее лишней объясняющей переменной, используя t-критерий: tкр = 2,021. Так как 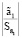= 0,237 и = 3,963, мы можем утверждать, что первый регрессор является незначимым (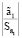 = 0,237 < tкр = 2,021). Значит, для нашей модели чистых доходов «Ак Барс» Банка. мы можем оставить только второй регрессор.

Для предполагаемой модели линейной парной регрессии в качестве контролирующей выборки возьмем три даты: 01.10.2008, 01.10.2013, 01.07.2017, что составляет 6,5 % статистики). Спецификация будет выглядеть следующим образом:

ЧДt = а0 + а1*КЛt + ut (3.1)

а0 > 0, а1 > 0.

По МНК (воспользуемся функцией ЛИНЕЙН) получим новые значения параметров:

ЧДt = 2449676 + 0,190*КЛt + ut (3.2)

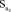= 709246; 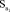= 0,045; σ = 2330854.

Проведем F-тест для модели (3.2):

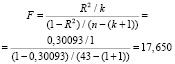
Fкр = F.ОБР.ПХ(0,05; 1; 41) = 4,079

Таким образом, F > Fкр => модель (3.1) является качественной. Поэтому продолжим работу с полученной моделью (3.2), проверим для неё выполнение предпосылок Гаусса-Маркова и адекватность.

1. Рассчитаем оцененные значения чистых доходов для каждого t. Вычислим значения ut и найдем оценку величины их математического ожидания. Она равна -0,0000000028, что говорит о выполнении первой предпосылки теоремы Гаусса-Маркова.

2. Проведем тест Голдфелда-Квандта для проверки предпосылки о гомоскедастичности случайных остатков модели. Упорядочим по возрастанию значения регрессора КЛ и разделим полученную таблицу на три части, где количество выборок в первой и третьей части n’ = 15. Оценим МНК модель по первой и третьей части и рассчитаем значения GQ и GQ-1, а также Fкр

0,031

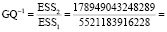32,411

Fкр = F.ОБР.ПХ(0,05; 13; 13)= 2,577

GQ < Fкр, но GQ-1 > Fкр => предпосылка не выполняется.

3. Проведем тест Дарбина-Уотсона для проверки предпосылки о некоррелируемости случайных остатков модели [4]. Вычислим значение статистики DW по формуле:

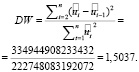
Значение dl = 1,44; du = 1,54.

Значение 1,5037 попадает в область М2 (между 1,44 и 1,54) => возникает неопределенность (ни принять, ни отклонить выполнение предпосылки мы не можем).

4. Предпосылка о Cov (ui; xli) = 0 выполняется, так как значения по всем предопределенным переменным заданы, а Cov (x; c) = 0.

Для устранения гетероскедастичности случаных остатков преобразуем исходные данные, разделив обе части модели (3.1) на значения регрессора КЛ [5]. Определим новый вид модели:

ЧДt/КЛt = а0*(1/КЛt) + а1 + ut/КЛt (4.1)

а0 > 0, а1 > 0.

Проведем замену переменных и переобозначение параметров и получим окончательный вид новой модели:

yt = b0 + b1*xt + vt (4.2)

b0 > 0, b1 > 0.

Получим новую таблицу данных для модели (4.2), которую и будем тестировать на гомоскедастичность. Оценим МНК модель по первой и третьей части, рассчитаем

GQ = 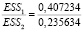= 1,728;

GQ-1 =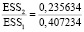 = 0,579;

Fкр = F.ОБР.ПХ(0,05; 13; 13) = 2,577.

Так как GQ < Fкр, GQ-1 < Fкр => предпосылка выполняется.

Таким образом, нам удалось устранить гетероскедастичность в модели. Проверим отсутствие автокорреляции случайных остатков в ней.

Значение DW = = 2,736, границы статистики dl = 1,44; du = 1,54.

Значение 2,736 попадает в область М5 (между 2,56 и 4), из чего следует наличие автокорреляции у остатков.

Преобразуем нашу модель для устранения автокорреляции методом ОМНК. Используем для этого авторегрессионный процесс первого порядка AR(1).

1. Используя AR(1) в качестве модели автокорреляции остатков, можно записать:

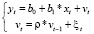(4.3)

2. Предполагая, что структура модели является постоянной, для периода t-1 получаем модель:

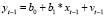(4.4)

Умножаем обе части уравнения (4.4) на ρ:

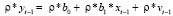(4.5)

3. Вычтем уравнение (4.5) из (4.3):

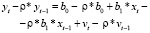(4.6)

4. Приводим уравнение (4.6) к виду:

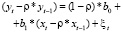(4.7)

где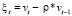

5. Введем новые обозначения:

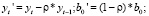
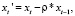где t ≥ 2 (4.8)

Мы получили преобразование Бокса-Дженкинса. Перепишем уравнение (4.7) в виде:

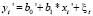(4.9)

Оценим значение ρ. Его можно определить несколькими способами, например, через статистику Дарбина-Уотсона: 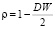= –0,368.

Находим МНК-оценки параметров модели (4.9) и рассчитаем статистику DW:

DW = 1,83 – попадает в промежуток М3 (между 1,54 и 2,46), следовательно, четвертая предпосылка теоремы Гаусса-Маркова выполняется.

Перепроверим гипотезу об отсутствии гетероскедастичности в модели (4.9):

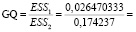1,429;

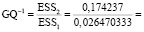0,700;

Fкр = F.ОБР.ПХ(0,05; 13; 13) = 2,577

GQ < Fкр, GQ-1 < Fкр => гипотеза принимается

Таким образом, мы получили выполнение всех предпосылок теоремы Гаусса-Маркова. Теперь мы можем записать окончательный вид модели и перейти к проверке ее адекватности.

Окончательный оцененный вид модели:

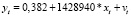(5.1)

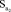= 0,038; 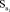= 223537; σu = 0,146,

где yt = ЧД/КЛ, xt = 1/КЛ.

Итак, проверим модель на адекватность по выделенной нами контролирующей выборке. Пересчитаем значения контролирующей выборки по схеме, приведенной в модели (5.1), то есть ЧДi/КЛi и 1/КЛi и рассчитаем оцененные значения результирующего показателя, учитывая значения (vt-1*ρ). Построим доверительные интервалы для каждой контролирующей выборки. Для этого рассчитаем ошибку прогноза :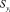

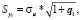
где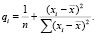

Используя в качестве нормы ошибки tкр = СТЬЮДЕНТ.ОБР.2Х(0,05;41), строим прогнозный интервал для каждого контрольного периода:

Все фактические значения результирующего показателя попадают в доверительные интервалы, значит модель (5.1) признается адекватной на 5 %-ом уровне значимости.

Таким образом, нами была получена адекватная модель прогнозирования чистых доходов банка. Все задачи, которые автор ставил перед собой в ходе данной работы были достигнуты: определен регрессор, который должен быть включен в модель; проверены предпосылки теоремы Гаусса-Маркова; устранены гетероскедастичность и автокорреляция остатков посредством метода ОМНК. Отметим, что стандартные ошибки оцененных коэффициентов являются довольно маленькими, что свидетельствует о эффективности полученных коэффициентов модели. Модифицированный вид модели, к которому мы пришли, несколько усложняет ее практическое использование, но простые математические преобразования, которые необходимо проделать со статистическими данными, легко выполнить с помощью Excel.

Модель может быть использована менеджментом «Ак Барс» Банка как инструмент прогнозирования чистого дохода банка в будущем. При имеющихся данных о ссудах, предоставленных клиентам, не являющихся кредитными организациями, руководство банка понимает, сколько процентных доходов банк получит от них. Однако, безусловно, представляется, что полученная модель (5.1) в будущем может быть модифицирована и уточнена.