science-review.ru
Актуальность изучения дисциплин «Эконометрика» и «Математическое моделирование природных процессов» в рамках образовательных программ обусловлена требованиями государственного образовательного стандарта – сформировать у обучаемых следующие компетенции:
- способность применять математический инструментарий для решения практических задач;
- способность строить стандартные теоретические и эконометрические модели, необходимые для решения профессиональных задач;
- анализировать и интерпретировать полученные результаты.
Цель исследования: выявление методических особенностей преподавания дисциплин «Эконометрика» и «Математическое моделирование природных процессов».
Материалы и методы исследования
Основная цель занятий по указанным дисциплинам – формирование и развитие умений и навыков построения и анализа моделей реальных экономических или природных явлений и процессов [1].
Свойство условных единиц (например, почвенных горизонтов на параллельных делянках полевого опыта) отличаться друг от друга даже в однородных совокупностях называется изменчивостью или варьированием.
Варьирующими признаками у растений являются их высота, содержание протеина, количество и масса зерен в колосе и др.; у почвы – рН, содержание Сорг, тяжелых металлов. Колебание, изменчивость, вариация – результат влияния различного сочетания внешних условий, не всегда поддающихся учету и определяемое часто как следствие случайных причин, вызывающих различия в изучаемых признаках. Следовательно, при любом исследовании данные опытов будут всегда варьировать в тех или иных пределах.
Варьирование признаков создает трудность в тех случаях, когда требуется дать общую характеристику определенной совокупности растений, почв, почвенных горизонтов и т. п. по отдельным признакам или сравнить две такие группы и найти различие между ними. Совершенно очевидно, что не всегда возможно исследовать по тому или другому признаку всю совокупность. В этих случаях прибегают к изучению части ее, по которой делают общее заключение.
Для успешного решения практических задач любого рода требуется грамотно формализовать имеющиеся массивы информации и сформировать из них данные для решения поставленной задачи; корректно сформулировать саму задачу исследования; построить модель процесса и провести анонсированное исследование; и, наконец, сделать выводы, корректно интерпретируя полученные математические результаты. В связи с появлением компьютеров исследование явлений и процессов методами математического моделирования занимает ведущее место среди других методов исследования.
Модель – это описание процесса или явления на формализованном языке. Такое описание особенно полезно, если исследование физически невозможно или затруднено.
Модели принято разделять на типы:
- регрессионные модели с одним уравнением
- временные ряды
- системы одновременных уравнений.
Регрессионные модели с одним уравнением – используются одномоментные данные по какому-либо показателю, полученные для однотипных объектов. Например, данные об урожайности на опытных делянках в зависимости от доз внесенного удобрения.
Временные ряды – данные об одном объекте, фиксирующие показатели процесса в динамике, т.е. в определенные последовательные моменты времени. Например, метеоусловия в вегетационный период.
Системы одновременных уравнений – занимают промежуточное положение: они отражают данные наблюдения за несколькими объектами. Например, дифференциальное уравнение продуцирования углерода СО2 разрешено относительно производной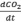 
. И эта производная входит в уравнение динамики общего органического вещества почвы
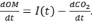
ОМ – органическое вещество (organic matter), I(t) – поступление свежего опада.
По зафиксированным данным предполагается постановка задачи. В качестве аргументов могут рассматриваться пространственные координаты: x – при проботборе вдоль линии; x, y – две координаты при площадном проботборе с конкретной глубины; x, y, z – при пространственном проботборе. В других задачах аргументом может быть время – при изучении сезонной динамики свойств почв. Задачи носят, как правило, двуединый характер – на основе анализа полученных данных создать модель рассматриваемого процесса и сделать прогноз его развития.
Проведение занятий должно быть направлено на интенсификацию и индивидуализацию обучения с применением интерактивных форм обучения.
Актуальной интерактивной формой лекций является лекция с разбором конкретных ситуаций (кейс-метод). Особенностью такого вида лекций является то, что преподаватель ставит на обсуждение не вопросы, а конкретную ситуацию из практической или будущей профессиональной деятельности обучающихся. Такая ситуация представляется в виде реальных экономических или природных данных. Обучающиеся анализируют и обсуждают эти микроситуации сообща, предлагая способы действия для разрешения представленной проблемы.
В целях обеспечения наглядности обучения, повышения уровня усвоения знаний, мотивации изучения дисциплины используются мультимедиа-средства и информационные технологии.
В различных экономических ситуациях применяются временные ряды. На занятиях рассматриваем выравнивание временного ряда методом экспоненциального сглаживания.
Для проверки знаний обучаемых проводится промежуточная аттестация в форме теста. Приводим примерные вопросы одного из тестов с; объем выборки n = 12; коэффициент детерминации R2 = 0,6; Fкр = 4,96 (при уровне значимости a = 0,05). Тогда вывод можно сделать на основе теста Фишера:
1) уравнение регрессии статистически значимо;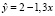 
; объем выборки n = 12; коэффициент детерминации R2 = 0,6; Fкр = 4,96 (при уровне значимости a = 0,05). Тогда вывод можно сделать на основе теста Фишера:
2) уравнение регрессии статистически незначимо;
3) отсутствует авто коррелированность остатков;
4) прогнозное значение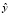 
при x = 1 равно 0,9.
1. Проверка наличия автокорреляции в остатках проводится с помощью:
1) теста Спирмена; 2) теста Фишера; 3) теста Стьюдента; 4) теста Дарбина-Уотсена.
2. Для оценивания параметров точно идентифицируемой системы одновременных эконометрических уравнений используется:
1) метод наименьших квадратов;
2) двухшаговый метод наименьших квадратов;
3) косвенный метод наименьших квадратов;
4) трехшаговый метод наименьших квадратов.
3. Между факторами X и Y существует слабая зависимость. Какой из коэффициентов корреляции свидетельствует об этом:
1) −0,65; 2) 0,1; 3) –0,95; 4) 0,25.
4. В чем заключается явление гетероскедастичности:
1) математическое ожидание остаточной компоненты равно нулю;
2) дисперсия остаточной компоненты равна нулю;
3) дисперсия остаточной компоненты постоянна;
4) дисперсия остаточной компоненты не постоянна;
6. Какое из перечисленных регрессионных уравнений получается по следующей группе данных: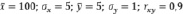 
.
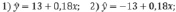
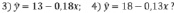
Теперь рассмотрим примеры дисциплины «Математическое моделирование природных процессов». Различают много видов мелиорации. Основными из них являются орошение, осушение, борьба с эрозией почв, фитомелиорация, химическая мелиорация. С развитием технического прогресса приемы мелиорации совершенствуются, разрабатываются новые технические средства регулирования воздушного, водного, питательного и теплового режимов почв [2].
При проведении мелиоративных исследований выполняются следующие наблюдения и исследования: метеорологические наблюдения; определение водно-физических свойств почвы (гранулометрический состав, наименьшая влагоемкость, влажность почвы, плотность сложения, плотность твердой фазы почвы, структура почвы,); определение агрохимических свойств почвы (содержание гумуса, содержание обменного калия, подвижного фосфора, нитрификационная способность и др.); определение содержания токсичных солей; содержание обменных оснований в почвенном поглощающем комплексе; уровень грунтовых вод; химизм грунтовых вод; фенологические и биометрические наблюдения [3].
Важнейшую роль в современной мелиоративной науке играют статистические методы исследований и обработки полученных данных. Эксперимент позволяет исследователю накопить факты, но это еще не решение проблемы. Накопленные факты следует анализировать [4].
Современные математические методы позволяют извлечь максимум информации из исходных данных. Математическая статистика изучает методы систематизации и обработки статистических данных. Используя результаты, полученные теорией вероятностей, позволяет не только оценить значения искомых характеристик, но и выявить степень точности выводов, получаемых при обработке исходных данных.
Пример. Определить среднюю плотность почвы по данным выборки, представленным в таблице [5].
Распределение плотности дерново-подзолистой почвы в пахотном слое
|
xi |
1,03 |
1,13 |
1,18 |
1,23 |
1,28 |
1,33 |
1,38 |
1,43 |
1,48 |
1,53 |
|
ni |
7 |
19 |
21 |
29 |
26 |
18 |
12 |
9 |
6 |
3 |
.
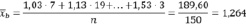Итак,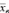 
= 1,264 – оценка средней плотности почвы по рассматриваемой выборке.
Выборочная дисперсия, вычисленная по n независимым наблюдениям над случайной величиной Х, не является несмещенной оценкой генеральной дисперсии S2, так как математическое ожидание оценки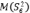 
не равно оцениваемому параметру S2, то есть выборочная дисперсия является смещенной оценкой для генеральной дисперсии [6]. Математическое ожидание 
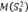отличается от S2 множителем 
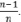При большом объеме выборки это различие не столь ощутимо. Если же объем выборки мал, то приходится выборочную дисперсию дополнить множителем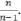 
Коэффициент вариации (изменчивости) V представляет отношение среднего квадратического отклонения к среднему арифметическому и выражается в процентах
.
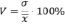Рассмотрим необходимость коэффициента вариации на примере. Пусть среднее квадратическое отклонение по результатам определений уровня грунтовых вод равно 5 см. Если средняя высота подъема уровня грунтовых вод равна 10 см, то σ = 5 см говорит о большой неоднородности в повторности измерений. Если же σ = 5 см получена при среднем уровне грунтовых вод в 250 см, то среднее квадратическое отклонение можно считать небольшим. Отсюда следует, что большое и малое значения среднего квадратического отклонения относительны. Для определенного суждения необходимо знать соответствующее среднее значение признака [7].
Рассмотрим доверительный интервал для оценки математического ожидания нормально распределенной случайной величины в случае малого объема выборки
По данным 9 измерений содержания физической глины (<0,01 mm) в гранулометрическом составе почвы найдены: средняя результатов измерений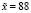 
и «исправленное» среднее квадратическое отклонение 
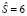. Найдите границы, в которых с надёжностью 0,99 заключено истинное значение измеряемой величины.
Среднее квадратическое отклонение результатов измерений неизвестно, поэтому для определения границ истинного значения воспользуемся доверительным интервалом:
,
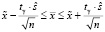где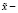 
выборочная средняя результатов измерений, 
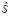– «исправленное» среднее квадратическое отклонение, n – объём выборки, tγ – найдём по таблице значений t-критерия при γ = 0,99 и n = n – 1 = 8 степеням свободы. t0,99 = 3,355. Тогда искомый доверительный интервал примет вид:
.
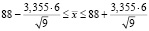После вычислений получим:
.
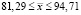Результаты исследования и их обсуждение
Практическая значимость дисциплин «Эконометрика» и «Математическое моделирование природных процессов» определяется тем, что применение разработанных методов позволяет выявить реально существующие связи между процессами и между показателями внутри сложного процесса; дать обоснованный прогноз развития процесса в заданных условиях; проверить эффективность построенной модели.
Изучение дисциплин предполагает приобретение обучающимися опыта построения математических моделей, принятия решения о спецификации и идентификации модели, выбора метода оценки параметров модели, интерпретации результатов, получение прогнозных оценок [8].
Заключение
Разработанный комплекс профессионально ориентированных задач показывает взаимосвязь специальных дисциплин и математики. В результате его применения у студентов формируются умения решать профессиональные задачи, используя математический аппарат [9–11]. Таким образом, особенности преподавания дисциплин «Эконометрика» и «Математическое моделирование природных процессов» – практико-ориентированность, учет особенностей будущей профессии, что составляет основу компетентностного подхода в преподавании математики [12].