Scientific journal

Научное обозрение. Педагогические науки

ISSN 2500-3402

ПИ №ФС77-57475

Понятие числа выступает фундаментальным понятием всего курса математики, поэтому знакомство с ним начинается с самой первой ступени образования – дошкольной. Математическая деятельность ребенка уже в детском саду связана с освоением им количественного и порядкового счета, состава чисел и сравнением рядом стоящих чисел в пределах десяти, с установлением соответствия между множеством и количеством элементов данного множества (его мощностью). На следующей ступени образования, в начальной школе, происходит формирование понятия бесконечного натурального ряда чисел и знакомство с дробными числами. Основное свойство числа, усваиваемое младшими школьниками, – это характеристика количества предметов, но в то же время число рассматривается ими как мера измерения величины, а свойства чисел (например, операция сравнения) определяются расположением числа в натуральном ряду. На последующих ступенях – основном и среднем общем образовании – рассматриваются числовые системы и их свойства. В связи с чем обучающиеся 5–11 классов изучают натуральные (N), целые (Z), рациональные (Q), действительные (R), комплексные (С) числа и их свойства. Изучение числовых систем в представленной последовательности соответствует историко-генетическому подходу развития понятия числа [1] или, другими словами, логической схеме, базирующейся на арифметике натуральных чисел [2]. Каждое последующее понятие числа расширяет предыдущее новыми видами чисел, т.е. каждое предыдущее рассматриваемое числовое множество является подмножеством следующего: N ⊂ Z ⊂ Q ⊂ R ⊂ С. Это можно проиллюстрировать с помощью диаграммы Эйлера (рисунок). Данный подход расширения понятия числа предпочитается в научных кругах [3, с. 19]. Отметим, что процесс расширения множества натуральных чисел продолжается и в настоящее время.

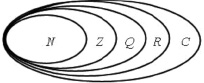
Расширение числовых множеств

Особую сложность в изучении представляют иррациональные числа (I), то есть те действительные числа, которые нельзя представить в виде дроби m/n, где m – целое, а n – натуральное числа. С точки зрения теории множеств множество иррациональных чисел является дополнением множества рациональных чисел до совокупности всех действительных чисел. Таким образом, справедливы соотношения: I = R\Q, Q∪I = R, Q∩I = {Ø}.

В свою очередь, иррациональные числа можно классифицировать как алгебраические и трансцендентные. К алгебраическим относятся все числа, которые являются корнями многочленов с целыми коэффициентами, например 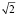– число иррациональное, но не трансцендентное, так как является корнем уравнения x2 – 2 = 0, а число p – трансцендентное.

Будущий учитель начальных классов должен уметь устанавливать взаимосвязи между числовыми множествами, понятием дроби, рациональными и действительными числами. Это способствует решению им проблемы преемственности в обучении математике, в частности изучения числовой линии в начальных и последующих классах школы в содержательном и методическом аспектах. Именно поэтому от преподавателя педагогического вуза требуется корректировка содержания дисциплины «Математика» с учетом более глубокого изучения темы «Расширение множества натуральных чисел», представленной небольшим объемом и, как правило, незначительным количеством часов в рабочей программе. Таким образом, целью исследования явились корректировка методики преподавания числовой линии студентам направления подготовки «Педагогическое образование» профиля «Начальное образование» в рамках дисциплины «Математика» и разработка системы заданий, направленной на формирование у студентов умений устанавливать вид числа, отношения между числовыми множествами.

Материалы и методы исследования

Несмотря на то, что задания вычислительного характера широко представлены в материалах государственных экзаменов по математике для 9-х и 11-х классов, преподаватели вуза зачастую сталкиваются с низким уровнем сформированности вычислительных навыков студентов. Так, результаты входного контроля и первые занятия по математике первокурсников направления подготовки «Педагогическое образование» профиля подготовки «Начальное образование» в Ставропольском государственном педагогическом институте показали следующее:

- 52 % студентов испытывают трудности в устном счете, предпочитая выполнять вычисления на калькуляторе; если преподаватель запрещает пользоваться калькулятором, то студенты прибегают к использованию письменных вычислений (сложение, вычитание, умножение в столбик, деление уголком), но при этом некоторые допускают ошибки;

- 69 % студентов испытывают трудности в установлении отношений между числовыми множествами,

- 72 % студентов ошибаются при определении вида числа.

Мы полагаем, что приблизительно такие результаты можно наблюдать не только у первокурсников педагогических вузов в силу того, что историко-генетический подход предусматривает линейное (поступательное) расширение понятие числа (рисунок), в то время как расширение понятия числа в школьном курсе математики строится по нелинейной модели: натуральные числа и ноль (N0 или Z+) → дробные положительные числа (Q+) → отрицательные целые числа (Z-) → дробные отрицательные числа (Q-) → рациональные числа (Q) → иррациональные (I) → действительные (R) → комплексные числа (С). Мы считаем, что в связи с нелинейностью изучения числовых систем у школьников слабо сформированы знания о каждом из числовых множеств, а также навыки определения вида числа, что имеет отражение при их дальнейшем обучении в вузе.

В учебнике «Математика» Л.П. Стойловой, специально предназначенном для реализации образовательных программ высшего образования по направлению подготовки «Педагогическое образование» профиль «Начальное образование», числовая линия излагается по следующей схеме: N → Q+ →R+ → R [4, с. 352]. Мы предлагаем изучение числовой линии с точки зрения теоретико-множественного подхода, согласно которому каждое новое множество получается дополнением предыдущего. При этом каждая новая система чисел или способствуют решению новых задач, или совершенствует уже известные решения, ведь с расширением множества чисел увеличивается и количество операций, выполнимых на нем (таблица).

Далее рассмотрим систему заданий по теме «Расширение множества натуральных чисел», направленную на формирование умений устанавливать отношения между множествами и на определение вида числа.

Задание 1. Выберите верные утверждения:

а) Q ⊂ R; б) R ⊂ Z; в) N ⊂ R; г) Z ⊂ Q;

д) N0 ⊂ N; е) Q ⊂ N; ж) N ⊂ N0; з) I ⊂ R.

Задание 2. Выберите верные утверждения. Точку зрения поясните.

а) всякое целое число – рациональное;

б) всякое рациональное число – целое;

в) всякое иррациональное число – действительное;

г) ноль – число натуральное;

д) ноль – число рациональное.

Задание 3. Опишите следующие множества: N0\N, Z\N, Z\N0, R\Q, R\I, Z+∪Z-, Z+\{0}, Q∪I, Q∩I, R∩Q, R∪Q.

Задание 4. Выберите верные утверждения.

а) 17 – число натуральное;

б) 17 – число действительное;

в) 17 – число рациональное;

г) 17 – число иррациональное.

Задание 5. Выберите верные утверждения.

а) 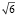– число натуральное;

б) 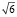– число действительное;

в) 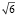– число рациональное;

г) 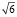– число иррациональное.

Задание 6. Какие числа являются натуральными: 0, 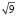, , 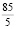–5, 10?

Задание 7. Выберите иррациональные числа: 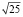; ; 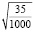e; p; .

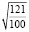При решении данного задания чаще всего используется следующее определение иррационального числа, известное еще в XVIII в.: иррациональным называется то число, из которого нельзя извлечь корень.

Задание 8. Какие из данных чисел являются иррациональными, а какие рациональными: , , , , , , , , , , ?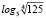

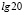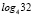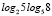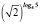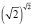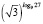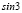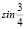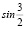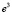Задание 9. Какие числа являются иррациональными: , , , ?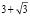

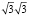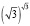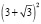Решение последнего задания помогает учащимся понять: в результате выполнения алгебраических операций над иррациональными числами можно получить как иррациональное число, так и рациональное, что не характерно для остальных числовых множеств. Так, на множестве целых чисел, как было указано ранее, всегда выполнимы операции сложения, умножения и вычитания, результат их выполнения применительно к целым числам также является целым числом.

Задание 10. Уравнение x + 3 = 2 не имеет решений …

а) на множестве целых чисел;

б) на множестве натуральных чисел;

в) на множестве рациональных чисел;

г) на множестве действительных чисел;

д) на множестве иррациональных чисел.

Задание 11. Постройте график функции y = x а) на множестве R; б) на множестве Z; в) на множестве N. Какое множество является областью значений функции в каждом случае?

В силу того, что ФГОС ВО по направлению подготовки «Педагогическое образование» предполагает реализацию программ бакалавриата в контексте профессиональной деятельности, то изучение студентами дисциплин должно проходить в осознании того, каким образом полученные знания, умения понадобятся, будут использоваться, помогут им в профессиональной деятельности. Согласимся с мнением З.А. Магомеддибировой [5] о необходимости проведения целенаправленной работы со студентами по выявлению связей между изучаемым математическим материалом и начальным курсом математики, а также мнением А.Л. Чекина [6] о возможности интеграции курсов математики и методики преподавания математики для эффективной профессиональной подготовки. Ввиду этого при изучении дисциплины «Математика» мы предлагаем задания студентам не только на отработку математических понятий, но и отражающие специфику профессиональной деятельности будущего учителя начальных классов [7]. В качестве примера такого вида заданий приведем проектную задачу на тему: «Расширение множества натуральных чисел в начальном курсе математики»:

1. Ознакомьтесь с Примерной основной образовательной программой начального общего образования. Каковы требования к планируемым результатам освоения подраздела «Числа и величины» предметной области «Математика и информатика»?

2. Изучите числовую линию учебно-методического комплекта (УМК) по математике для начальной школы (выбор УМК на усмотрение студента, но из федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования) и ответьте на вопросы:

1) Как в учебниках по математике для начальной школы объясняется, что такое натуральное число?

2) Как определяется число нуль в начальном курсе математики?

3) Какие действия с нулем должны знать учащиеся начальных классов?

4) Как определяются доли и дроби в начальном курсе математики?

5) Какие действия с дробями должны научиться выполнять учащиеся начальных классов?

6) Описаны ли в школьных учебниках математики для 1–4 классов причины расширения множества натуральных чисел? Как бы Вы объяснили обучающимся причины расширения множества натуральных чисел?

3. Какие и каким образом можно формировать универсальные учебные действия у учащихся начальной школы при ознакомлении их с расширением множества натуральных чисел?

Результаты исследования и их обсуждение

Проведенное исследование преподавания бакалаврам педагогического образования профиля подготовки «Начальное образование», т.е. будущим учителям начальных классов, темы «Расширение множества натуральных чисел» в рамках дисциплины «Математика» с использованием разработанных нами методики и системы заданий, позволило получить следующие результаты:

– повышение качества знаний по изучаемой теме за счет реализации разработанной методики с использованием системы заданий, направленной на формирование умений устанавливать отношения между множествами и на определение вида числа;

– понимание студентами взаимосвязи изучаемого материала с практикой обучения младших школьников математике за счет выполнения проектных задач;

– повышение уровня мотивации студентов к изучению дисциплины «Математика» за счет практико-ориентированных заданий, позволяющих увидеть возможности применения получаемых знаний в реальной педагогической деятельности;

– более успешное прохождение студентами педагогических практик за счет проработки школьных учебников математики.

Отметим, что в процессе обучения математике в педагогическом вузе формируются, прежде всего, специальные компетенции (СК), которые отражают специфику конкретной предметной области (математики) в профессиональной деятельности. Несомненным достоинством разработанных нами методики и системы заданий в процессе их реализации при обучении студентов является возможность формирования профессиональных (ПК), общепрофессиональных (ОПК) и общекультурных (ОК) компетенций, заложенных в Федеральном государственном образовательном стандарте высшего образования [8, с. 9], а именно: общекультурных – 4, 5, 6; общепрофессиональных – 1 и профессиональных – 1, 2, 4, 6, 10.

Заключение

Умение работать с числами не только способствует формированию теоретико-множественных представлений, но и развивает представления о числовых функциях, тождественных преобразованиях, что определяет необходимость формирования данного умения. Преподавание темы «Расширение множества натуральных чисел» будущим учителям начальных классов на базе разработанных нами методики и системы заданий показывает повышение уровня знаний и умений студентов в рамках изучения числовой линии.