science-review.ru
В настоящее время высшее образование должно способствовать формированию специалистов широкого профиля, сочетающему глубокие фундаментальные знания и обстоятельную практическую подготовку конкретной отрасли производства. В КубГАУ работа над курсом «Математическое моделирование процессов в компонентах природы» продолжается. Новизна исследований заключается в составлении примеров прикладного характера, которые усиливают взаимосвязь математики и смежных дисциплин, формируют у студентов умение строить математические модели, обеспечивают профессиональную направленность обучения [1].
Цель исследования – разработать программу дисциплины «Математическое моделирование процессов в компонентах природы» с примерами из данной специальности.
Результаты исследования и их обсуждение
Приведем несколько примеров прикладного характера, которые показывают применение теории вероятностей.
Первый пример. Рассматриваем популярные статистические критерии.
Критерий Стьюдента. Проблема ставится следующим образом. Пусть имеется две случайные величины ζ и η. Обе они являются нормальными случайными величинами, дисперсия их также одинакова, то есть D{ζ} = D{η} = σ2. А математические ожидания M{ζ} = a1 и M{η} = a2 могут быть разными. Необходимо проверить гипотезу Н0: а1 = а2 при альтернативе Н1: а1 ≠ а2.
Пусть в n1 опытах измеряли величину ζ, получили значения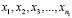 
; в n2 опытах измеряли величину η и получили значения 
.
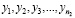Оценки величин а1 и а2 имеют вид
, 
.
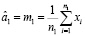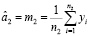Рассмотрим их разность т1 – т2. Пусть верна гипотеза Н0. Что тогда можно сказать об этой разности?
Так как при Н0 а1 = а2, то
М{m1 – m2} = М{m1} – M{m2} = 0.
Далее, так как
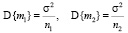, то
.
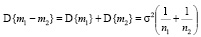Поэтому дробь
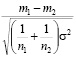
является стандартной нормальной случайной величиной с нулевым математическим ожиданием и единичной дисперсией.
Но величина σ2 неизвестна, её надо заменить оценкой. Какая же она?
Оценка величины σ2 по первой выборке есть
,
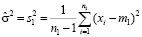а по второй выборке –
.
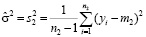Из этих двух величин надо скомбинировать одну общую оценку величины σ2.
Стьюдент предложил брать её в виде
,
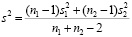так как в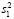 
есть сомножитель 
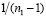, а в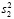 
– сомножитель 
.
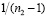Заменяя в выражении для σ2 её оценкой s2, получим величину
.
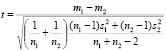Можно доказать, что при верности гипотезы Н0 величина t имеет распределение Стьюдента с числом степеней свободы f = n1 + n2 – 2.
Далее представим α0 в виде
α0 = α0/2 + α0/2
и найдём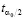 
, соответствующее числу степеней свободы f = n1 + n2 – 2. Если верна гипотеза Н0, то событие, заключающееся в выполнении неравенства 
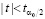будет иметь вероятность 1 – α0, а событие 
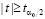будет наступать с вероятностью α0, то есть будет событием практически невозможным. Поэтому решающее правило имеет вид: если выполнится условие 
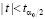, то надо принять гипотезу Н0; если же окажется, что 
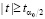, то гипотеза Н0 должна быть отвергнута.
Использование критерия Стьюдента описано во втором примере.
Основным недостатком критерия Стьюдента является то, что он «привязан» к нормальному распределению. Поэтому в настоящее время большое распространение получили так называемые непараметрические критерии, которые «свободны» от вида функции распределения выборочных значений, то есть их можно применять для любых функций распределения.
Большинство таких критериев основано на том, что измеренные значения заменяются их рангами.
Пусть имеется выборка из пяти значений, которые равны 7,7; 6,8; 8,3; 7,5; 8,9. Расположим их в порядке возрастания и пронумеруем в этом порядке
Эти порядковые номера и называют рангами соответствующих выборочных значений.
А что делать, если некоторые выборочные значения совпадают между собой? Вообще-то говоря, для непрерывных случайных величин такое совпадение имеет вероятность 0, но оно может иметь место из-за ограниченной точности измерений и округления полученных результатов.
В этом случае совпадающим выборочным значениям в качестве их рангов присваивается среднее арифметическое их рангов. Например, если выборочные значения равны 7,5; 6,8; 8,3; 7,5; 8,9, то их ранги будут такими:
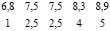
Рассмотрим критерий Вилкоксона. Пусть имеются выборки случайных величин ζ и η:
х1, х2, х3, …, хm и y1, y2, y3, …, yn.
Критерий Вилкоксона проверяет гипотезу об однородности выборок, то есть гипотезу следующего вида: Н0: ∀x F ζ(x) = F η(x) при альтернативе Н1: ∃ x F ζ(x) ≠ F η(x). Для её проверки составим из величин х1, х2, х3, …, хm и y1, y2, y3, …, yn. один общий вариационный ряд, то есть расположим их в порядке возрастания их значений. В результате получим последовательность типа
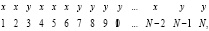
где N = m + n. Заметим, что сами выборочные значения выписывать не надо, надо лишь писать буквы х и у в зависимости от того, к какой выборке они принадлежат.
В критерии Вилкоксона в качестве статистики для проверки гипотезы используется сумма рангов той выборки, объём которой меньше. Пусть, например, т < п и r1, r2, r3, … , rm есть ранги, соответствующие значениям х. Тогда статистика критерия Вилкоксона задаётся формулой
W = r1 + r2 + r3 + ... + rm.
Само решающее правило имеет вид если выполнено условие
W1 ≤ W ≤ W2,
то гипотеза Н0 принимается, в противном же случае она отвергается.
Величины W1 и W2 находятся из специальных таблиц в соответствии с объёмами выборок т и п и уровнем значимости α0. В таблицах обычно приводится лишь величина W1, а величину W2 считают по формуле
W2 = m(m + n + 1) – W1.
Рассматриваем еще один популярный статистический критерий – так называемый критерий серий. Его обычно применяют при выравнивании экспериментальных данных к некоторым кривым по методу наименьших квадратов.
Пусть данные измерений имеют вид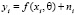 
и, выравнивая данные к зависимости y = f (x, θ), получили выровненные значения 
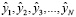. Будем сравнивать их с экспериментальными данными 
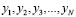и, если 
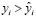, то приписывать этой паре знак + , если же 
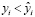, то знак минус. В результате получим последовательность знаков + и – вида
+ + – + + + – – – – … + – – ,
состоящую из т элементов + и п элементов –.
Проверяется гипотеза о том, что эти элементы расположены случайно. Если эта гипотеза будет принята, то говорят, что опытные данные не противоречат выровненным значениям; в противном случае считают, что опытные данные противоречат выровненным значениям и необходимо выравнивать их к какой-то другой кривой.
Сам критерий выглядит следующим образом. Назовём сериями части нашей последовательности, каждая из которых состоит из знаков одного вида.
Пусть γ есть общее количество серий в нашей последовательности. Тогда по таблицам критерия серий при заданном уровне значимости α0 находим величины γ1 и γ2, и если окажется, что γ1 < γ < γ2, то принимается гипотеза о том, что выровненные значения не противоречат экспериментальным данным. Если же окажется, что γ ≤ γ1 или γ ≥ γ2, то считается, что выровненные значения противоречат экспериментальным данным и надо их выравнивать к какой-то другой кривой.
Обычно действуют по следующей схеме. Сначала данные выравнивают к прямой линии, то есть к полиному порядка 1. Затем, используя критерий серий, проверяют, противоречат выровненные значения экспериментальным данным или нет. Если не противоречат – то на этом всё заканчивается. Если же противоречат – то выравнивают данные к полиному второго порядка, снова проверяют гипотезу о случайности + и –, и в случае противоречия выравнивают к полиному третьего порядка и т.д. Та степень полинома, при которой в первый раз критерий серий показывает, что нет противоречия между экспериментальными и выборочными значениями, и принимается в качестве результата выравнивания.
Второй пример. Для характеристики температурного режима территории вычисляем основные статистические характеристики рядов метеопараметров: абсолютные минимальную и максимальную суммы температур, интервал между абсолютными максимальной и минимальной суммами температур, коэффициенты асимметрии, эксцесса и вариации [2].
Помимо расчета обычных статистических показателей необходимо проводить углубленный анализ временных рядов с применением математического моделирования. Такой методологический подход позволяет получить дополнительную информацию, необходимую для оптимального планирования и организации сельскохозяйственного производства [3].
Пространственно-временную изменчивость исследуем с помощью аппарата разложения полей по естественным ортогональным составляющим. Система функций для разложения подбирается по специфике рассматриваемого поля. Этот математический аппарат позволяет полнее представить начальную информацию, а еще и уменьшить число предикторов.
Исследуем временную структуру суммы температур за вегетационный период в низкоурожайные и высокоурожайные годы. Оценка значимости выявленных отличий осуществляется с помощью критерия Стьюдента. Если полученное значение критерия больше табличного на заданном уровне и числе степеней свободы, то исследуемые выборки статистически различаются между собой.
Третий пример. Рассматриваем характеристики зависимости случайных величин друг от друга. Пусть дана двумерная случайная величина (ζ, η) с плотностью вероятностей рζη(х, y). Ковариацией величин ζ и η называется величина
.
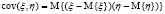Эта характеристика называется корреляционным моментом (иначе «моментом связи») случайных величин.
Наиболее полно зависимость случайной величины ζ от η описывается условной плотностью вероятностей рζ|η(х|y). Зависимость η от ζ – условной плотностью вероятностей рη|ζ(y|x). Однако эти плотности вероятностей сложны для экспериментального измерения, и с ними трудно работать [4].
Вместо них рассматриваем так называемые условные математические ожидания (условные средние)
,
.
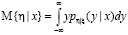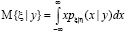В отличие от М{ζ} и М{η} это уже не числа, а функции. Кривую М{η| х} как функцию от х называют кривой регрессии η от ζ, а М{ ζ| y}, являющейся функцией от y, называют кривой регрессии ζ от η [5; 6].
Обычно этим кривым дают следующую наглядную, хотя и упрощенную трактовку [6]. В природе есть какая-то детерминированная зависимость, скажем η = f (ζ). Но сама же природа на эту зависимость «накидывает» случайные факторы, так что эта зависимость как бы размывается. А кривая регрессии и есть эта истинная зависимость, «очищенная» от всех случайных факторов.
Выводы
На современном этапе происходящих преобразований в образовании математические методы становятся необходимыми для всех направлений научной и практической деятельности специалиста. Потому при изложении курса «Математическое моделирование процессов в компонентах природы» мы стараемся выработать у студентов математический подход к изучению задач их специальности.
Студенты с большим интересом решают прикладные задачи. Такой подход направлен на повышение эффективности образовательного процесса и образовательного уровня подготовки студентов.