Scientific journal

Научное обозрение. Педагогические науки

ISSN 2500-3402

ПИ №ФС77-57475

В условиях действия ФГОС ООО основное внимание исследователей обращено к проблеме формирования универсальных учебных действий.

Сущность овладения обучающимися универсальными учебными действиями заключается в формировании способности к саморазвитию и самосовершенствованию путем сознательного и активного присвоения социального опыта. Универсальные учебные действия являются основой умения учиться, успешного усвоения новых знаний, умений и навыков.

Познавательные универсальные учебные действия оказывают огромное влияние на формирование учебно-познавательной деятельности школьников и познавательное развитие в целом. В процессе познавательного развития происходит формирование у учащихся научной картины мира, развитие умений управлять познавательной деятельностью, способов познания, развитие всех познавательных процессов, а также рефлексии. В своей книге, к числу познавательных универсальных учебных действий А.Г. Асмолов относит: «общеучебные действия, логические действия, а также действия постановки и решения проблемы» [1, с. 29].

Учебный предмет «Математика» имеет большие потенциальные возможности для формирования всех видов УУД. Реализация этих возможностей на этапе начального математического образования зависит от способов организации учебной деятельности школьников, которые позволяют не только обучать математике, но и воспитывать математикой, не только учить мыслям, но и учить мыслить.

Методологическую основу исследования составляют: концепции формирования универсальных учебных действий (А.Г. Асмолов [1], В.В. Давыдов, В.Г. Бурменская, О.А. Карабанова, Г.А. Цукерман); исследования, раскрывающие особенности познавательного развития в школьном возрасте (Подласый И.П. [4], Аникеева Н.В., Смоленцева А.А. [5]).

Универсальные учебные действия существовали всегда, работа над ними проводилась в советской школе на всех учебных предметах, но при традиционной системе обучения, в основе которой лежала репродуктивная модель обучения (передача знаний учителем учащимся), их называли по-другому: знания, умения, навыки. При репродуктивной модели школа могла и давала прочные знания, но, как показывает время, это малоприменимые на практике знания.

Как подчеркивает Н.М. Горленко в своей книге: «основное назначение универсальных учебных действий или их функция заключается, по мнению ряда исследователей, в том, чтобы обеспечивать возможности учащихся самостоятельно осуществлять деятельность учения. Это подразумевает, что ученик становится способен самостоятельно ставить учебные цели, планировать свою деятельность, выбирать способы достижения поставленной цели, осуществлять контроль и оценку результатов своей деятельности» [2, с. 26].

Универсальные учебные действия (УУД) – это действия, обеспечивающие овладение ключевыми компетенциями, составляющими основу умения учиться.

Приоритетом начального общего образования является формирование общеучебных умений и навыков, уровень освоения которых в значительной мере предопределяет успешность всего последующего обучения. Выделение в стандарте межпредметных связей способствует интеграции предметов, предотвращению предметной разобщенности и перегрузки обучающихся. Развитие личностных качеств и способностей школьников опирается на приобретение ими опыта разнообразной деятельности: учебно-познавательной, практической, социальной. Поэтому в стандарте особое место отведено деятельностному, практическому содержанию образования, конкретным способам деятельности, применению приобретенных знаний и умений в реальных жизненных ситуациях. Начальное общее образование призвано помочь реализовать способности каждого и создать условия для индивидуального развития ребенка.

Основным средством формирования познавательных УУД в курсе математики являются вариативные по формулировке учебные задания (объясни, проверь, оцени, выбери, сравни, найди закономерность, верно ли утверждение, догадайся, наблюдай, сделай вывод), которые нацеливают обучающихся на выполнение различных видов деятельности, формируя тем самым умение действовать в соответствии с поставленной целью. Учебные задания побуждают детей анализировать объекты с целью выделения их существенных и несущественных признаков; выявлять их сходство и различие; проводить сравнение и классификацию по заданным или самостоятельно выделенным признакам (основаниям); устанавливать причинно-следственные связи; строить рассуждения в форме связи простых суждений об объекте, его структуре, свойствах; обобщать, т.е. осуществлять генерализацию для целого ряда единичных объектов на основе выделения сущностной связи.

В Федеральном государственном образовательном стандарте основного общего образования (далее – Стандарт) прописаны конкретные требования к результатам освоения основной образовательной программы начального общего образования. Все результаты делятся на три группы: личностные; метапредметные; предметные.

В школьном возрасте ведущей формой деятельности становится учение. Но, несмотря на это, игра продолжает занимать важное место и оказывать положительное влияние на формирование личности школьника и познавательное развитие в частности. Многие исследователи, раскрывавшие важную роль игры в развитии детей, отмечали, что, воздействуя на учащихся эмоционально, игры активизируют мыслительную деятельность учащихся, благодаря играм учебный процесс становится более привлекательным и интересным.

И.П. Подласый в своем учебнике отмечал: «обобщая накопленный в школе опыт, выделяет ряд положительных моментов использования учебных игр:

- в процессе игр ученики овладевают опытом поведения в реальных жизненных ситуациях;

- игра дает возможность самим ученикам решать проблемы, а не оставаться пассивными наблюдателями;

- игра предоставляет хорошие возможности для переноса знаний и опыта деятельности из учебной ситуации в реальную;

- игры увлекают школьников: даже те учебные темы, которые обычно не вызывают интереса, легко усваиваются в игровой форме.

Однако в играх есть отрицательные моменты, которые существенно сужают диапазон их применения:

- кажущаяся простота и доступность игр;

- необходимость высокой профессиональной подготовки педагогов;

- потребность в больших затратах времени по сравнению с более экономными методами (например, чтением);

- возможность вспышки эмоций учеников, ухудшение их поведения, нередко до степени неконтролируемого;

- ограниченность порой численности участников игры, невозможность использовать ее для фронтального обучения» [5, с. 196].

Таким образом, в исследовании мы будем использовать дидактическую игру как средство формирования познавательных учебных действий. Игра может выступать эффективным средством развития познавательных универсальных учебных действий в школьном возрасте. Этому способствует реализация следующих условий: подбор комплекса дидактических игр; отбор содержания игр и четкое следование этапам проведения игры.

Теоретический анализ проблемы исследования показал, что формирование познавательных универсальных учебных действий в школьном возрасте является одной из важнейший задач в свете внедрения Федеральных государственных образовательных стандартов. В связи с этим нами были выделены познавательные учебные действия такие, как:

1) подводить под понятие (формулировать правило) на основе выделения существенных признаков;

2) владеть общими приемами решения задач, выполнения заданий и вычислений:

а) выполнять задания с использованием материальных объектов (счетных палочек, указателей и др.), рисунков, схем;

б) выполнять задания на основе рисунков и схем, выполненных самостоятельно;

в) выполнять задания на основе использования свойств арифметических действий;

3) самостоятельно проводить сравнение, сериацию, классификацию, выбирая наиболее эффективный способ решения или верное решение (правильный ответ);

4) строить объяснения в устной форме по предложенному плану;

5) использовать (строить) таблицы, проверять по таблице;

6) выполнять действия по заданному алгоритму;

7) строить логическую цепь рассуждений.

Задания, позволяющие научиться подводить под понятия на основе выделенных существенных признаков

Задание 1. Из какого числа маленьких кубиков состоит кубик, изображенный на рисунке?

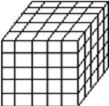
Если взять 1000 таких кубиков, как на рисунке, составить из них один большой куб, как с помощью произведения записи числа маленьких кубиков, из которых состоит построенный большой куб?

Вычисли значение этого произведения, используя правило умножения на число 1000. Объясни, почему справедливо данное неравенство.

1000*1000 = 1000000.

Как называется число, которое получается в результате увеличения числа 1000 в 1000 раз?

Сколько раз нужно сложить число 1000 с самим собой, чтобы получилось число МИЛЛИОН?

Алгоритм выполнения:

- Предлагаем учащимся прочитать задание, а затем внимательно рассмотреть рисунок и ответить на вопрос: из какого числа маленьких кубиков состоит кубик, изображенный на рисунке?

Ожидаемый ответ: в одном слое – 100 кубиков, но поскольку слоев 10, то кубик состоит из 1000 кубиков (100·10 = 1000).

- Продолжаем рассуждение: если взять 1000 таких кубиков и составить из них один большой куб, то с помощью произведения можно записать число маленьких кубиков, из которых состоит построенный большой куб. В большом кубе будет содержаться 1000 раз по 1000 маленьких кубиков, то есть 1000 · 1000 (кубиков).

- Предлагаем найти значение произведения, используя правило записи числа, которое в тысячу раз больше данного:

1000 · 1000 = 1000000.

Вспоминаем правило: чтобы записать число в 1000 раз больше данного, нужно к записи этого числа приписать справа три нуля.

- В заключение учащиеся отвечают на вопросы учебника.

- Как называется число, которое получилось в результате увеличения числа 1000 в 1000 раз? (Миллион.)

- Сколько раз нужно сложить число 1000 с самим собой, чтобы получить миллион?

(Тысячу раз: 1000 + 1000 + 1000 + … + 1000 = 1000 · 1000.)

Задание 2. Сколько разрядов содержит таблица, которая состоит из двух классов: классов единиц и класса тысяч? Какое минимальное число разрядов должно быть в таблице, чтобы в ней можно было записать число 1000000?

Рассмотрите данную таблицу и скажите, какой по счету справа разряд называется РАЗРЯДОМ ЕДИНИЦ МИЛЛИОНОВ.

Алгоритм выполнения:

Школьники читают задание и дают ответы на вопросы учебника.

• Просим рассмотреть таблицу разрядов и указать место разряда единиц миллионов.

• Разряд единиц миллионов находится на 7-м месте, считая справа налево.

Задание 3. Перечертите в тетрадь данную таблицу разрядов и классов. Запишите в этой таблице число 257689245.

Задания позволяющие владеть общими приемами решения задач, выполнение заданий и вычислений (выполнять задания на основе использования свойств арифметических действий)

Задание 1. Запишите следующие числа в порядке возрастания

256358975 35698712 9699697 256358969

3569872 9699997 25638969 6996979

Предварительно предлагаем алгоритм деятельности:

– соблюдая поразрядный принцип, записать числа в столбик;

– разбить запись каждого числа на классы с помощью знака ` и рядом поставить

порядковый номер с учетом порядка возрастания (убывания);

– записать числа в строчку, соблюдая найденную нумерацию.

Проверяем правильность выполнения задания, читая числа по цепочке:

3 569 872, 6 996 979, 9 699 697, 9 699 997, 25 638 969, 35 698 712,

256 358 969, 256 358 975.

Задание 2. Запишите следующие числа в порядке убывания.

5264837 62348927 21396 4587369

98632475 2138657 458231 69371452

Предварительно предлагаем алгоритм деятельности:

– соблюдая поразрядный принцип, записать числа в столбик;

– разбить запись каждого числа на классы с помощью знака ` и рядом поставить

порядковый номер с учетом порядка возрастания (убывания);

– записать числа в строчку, соблюдая найденную нумерацию.

Проверяем правильность выполнения задания, читая числа по цепочке:

98 632 475, 69 371 452, 62 348 927, 5 264 837, 4 587 369, 2 138 657,

458 231, 217 396.

Задания позволяющие проводить сравнение, сериацию, классификации, выбирая наиболее эффективный способ решения или верное решение (правильный ответ)

Задание 1. Назовите натуральное число, которое находиться между числами 458963 458961.

Алгоритм выполнения:

Запишите ответ с помощью верного двойного неравенства.

Задание 2. Следующие числа запишите в порядке возрастания

23654 687369 96542 142578 68736

Предварительно предлагаем алгоритм деятельности:

– соблюдая поразрядный принцип, записать числа в столбик;

– разбить запись каждого числа на классы с помощью знака ` и рядом поставить порядковый номер с учетом порядка возрастания (убывания);

– записать числа в строчку, соблюдая найденную нумерацию.

Проверяем правильность выполнения задания, читая числа по цепочке:

23654 68736 96542 142578 687369

Задания на построение объяснения в устной форме по предложенному плану

Задание 1. Из перечисленных примеров выберите те, при которых используется числа класса миллиардов:

а) число жителей России,

б) число жителей земли,

в) состояние самых богатых людей в мире,

г) расстояние от Земли до Солнца (км),

д) расстояние от Земли до Солнца (м).

Алгоритм выполнения:

- Проводим беседу о том, где нам могут встретиться большие числа класса миллиардов. Слушаем учащихся и подтверждаем (опровергаем) высказанные предположения (ученики могут называть в качестве примера число звезд в галактиках, число молекул в любом живом организме, число жителей Земли, а также состояние самых богатых людей в мире, ориентируясь на то, что их называют миллиардерами).

- Рассматривая примеры из астрономии, предлагаем обратиться к словарю. Приходим к выводу, что расстояние от Земли до Солнца (около 150 млн км)будет подходящим примером при условии выражения данного числа в метрах.

- Предлагаем самостоятельно выразить в метрах 150 000 000 километров.

- Проверяем на доске:

1 км = 1000 м 150 000 000 км = 1км · 150 000 000 = = 1000 м · 150 000 000 = 150 000 000 000 м

Задания, при которых нужно использовать таблицы или проверять по таблице

Задание 1. Запишите самое большое шестизначное число, в записи которого три раза встречает цифра 1.

Предлагаем ученикам с помощью разрядной таблицы записать шестизначное число, каждая цифра записи которого совпадает с номером разряда, следующего за разрядом, в котором она находится (765432).

Алгоритм выполнения:

- Просим учащихся придумать подобные задания и предложить их для выполнения в классе. Например, записать пятизначное число, каждая цифра записи которогосовпадает с номером разряда, в котором она находится (54321).

Предлагаем учащимся с помощью разрядной таблицы записать самое большое шестизначное число, в записи которого три раза встречается цифра 1.Вспоминаем, что наибольшее число получится только тогда, когда, начиная со старшего разряда, все разряды заполнятся самыми большими возможными числами.

Учащиеся конструируют искомое число.

Ожидаемый ответ: в первых трех старших разрядах можно записать цифру 9.

В оставшихся трех разрядах нужно записать цифру 1, так как другой возможности использовать три раза цифру 1 уже не будет. Если же цифру 1 записать ранее, то полученное шестизначное число будет меньше, чем то, запись которого начинается трех девяток.

Делаем вывод, что искомое число – 999111.

Задание 2. Запиши число 1111111 в таблицу разрядов в тетради. Представь это число в виде суммы разрядных слагаемых. Заключи в скобки слагаемые, которые относятся к классу единиц. Заключи в скобки слагаемые, которые относятся к классу тысяч.

Алгоритм выполнения:

Просим одного из учеников записать число 1111111 в таблицу разрядов, котораяспроецирована на доску.

- Предлагаем всем ученикам представить число 1111111 в виде суммы разрядных слагаемых.

- Проверяем на доске:

1111111 = 1000 000 + 100 000 + + 10 000 +1000 + 100 + 10 + 1.

- Заключаем в скобки слагаемые, которые относятся к классу единиц и к классу тысяч:

1111111 = 1 000 000 + (100 000 + 10 000 + + 1 000) + (100 + 10 + 1).

- Просим подчеркнуть слагаемое, которое не входит в первые два класса.

- Сообщаем, что это слагаемое относится к третьему классу – классу миллионов.

- Предлагаем перечислить разряды в новом классе.

Задания на выполнения по заданному алгоритму

Задание 1. 2354*47 3187*32 4823*26

Алгоритм выполнения:

Расположи полученные результаты в порядке возрастания.

Просим учащихся самостоятельно вычислить значения сумм.

Оказываем педагогическую поддержку тем, кому она необходима.

Организуем самопроверку по образцу с помощью листа для самопроверки.

Задание 2. Выполните сложение столбиком.

23568 + 4365 + 568

3072 + 86532 + 365645

6156 + 4104 + 8208

Алгоритм выполнения:

Просим учащихся самостоятельно вычислить значения сумм, записав числа строго поразрядно.

Оказываем педагогическую поддержку тем, кому она необходима.

Организуем самопроверку по образцу с помощью листа для самопроверки.

Задания на логическое построение цепи рассуждения

Задание 1. Найдите закономерности и назовите пропущенные числа.

Алгоритм выполнения:

После того как дети выполнили задание, отработали навык и осознали закономерность, ученикам предлагается работа в парах. Каждый ученик создает свою числовую цепочку закономерностей. Затем ученики меняются тетрадями и выполняют задание соседа. Меняются тетрадями еще раз и проверяют своего соседа.

а) 15290, 15291, 15292, ….., 15294, ……., …….;

б) 40 800, 40700, ……, 40500, ……, ………;

в) 192010, 182010, 172010, …….., ………, …….;

Задание 2. Эта диаграмма показывает, сколько примерно людей живет на некоторых материках. В Северной Америке – 498 325 00 человек, Южной Америке – 385 743 000 человек, Австралии – 22 363 человек. Отрезком, какого цвета обозначено число жителей каждого материка?

На основе диаграммы учащиеся могут ответить на вопрос, используя логику. Если этого не удалось сделать, то можно применить вычисления.

Целью констатирующего эксперимента выступала проверка уровня сформированости познавательных универсальных учебных действий у школьников на уроках математики. Исследование проводилось в образовательных учреждениях г. Лесосибирска.

По итогам контрольного среза, выполнив качественный и количественный анализ работ учащихся, мы пришли к следующим выводам: с первым и вторым заданием, подводить под понятие на основе выделения существенных признаков и владение приёмами решение задач, выполнения заданий и вычислений: справились многие учащиеся (68 %). Следовательно, у большинства учащихся сформировано умение подводить под понятие на основе выделения существенных признаков и умение решение задач. С третьим заданием, на проведение сравнение, сериацию, классификацию – 47 % учащихся. Это свидетельствует о том, что лишь половина учащихся владеют этим умением, учителю необходимо чаще применять задания такого типа для формирования данного умения. С четвертым заданием, на построение объяснений в устной форме по предложенному плану, справилось всего 37 % учащихся. Школьники не умеют строить объяснения в устной форме, необходимо провести дополнительную работу с учащимися на объяснение системы работы с планом и устным ответом. С пятым заданием, на использование таблицы и проверку по таблице, справилось меньше всего, 26 % учащихся. Этот результат говорит о том, что учителю стоит обратить внимания на задания с таблицами, так как это задание явилось самим трудным для учеников. С шестым заданием, на выполнения действий по заданному алгоритму, справилось наибольшее количество учащихся, 94 %. Самый высокий показатель, свидетельствует о том, что умение хорошо сформировано. С седьмым заданием, на построение логической цепи рассуждений, справились 57 % учащихся. Это средний показатель, учителю стоит обратить на это внимание и как можно чаще обращаться к заданиям на развитие логики. Результаты представлены на рис. 1.

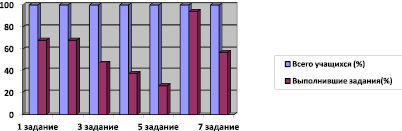
Рис. 1. Результаты контрольного среза

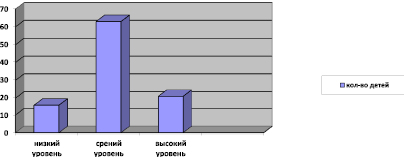
Рис. 2. Распределение учащихся по результатам контрольного среза

Для выявления высокого, среднего и низкого уровней сформированности умений следует применить следующие формулы:

верхняя граница = М + ?d,,

нижняя граница = M – ? d,

Где М – среднее арифметическое, d – среднее линейное отклонение.

Среднее линейное отклонение рассчитывается по формуле

Среднее линейное отклонение = ,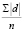

где Σ (сигма) – сумма; |d| – абсолютное значение каждого индивидуального отклонения от средней арифметической; n – число данных в ряду.

Среднее арифметическое:

(6 + 5 + 3 + 2 + 4 + 4 + 2 + 3 + 3 + 5 + 6 + 2 + 7 + 2 + 5 + 3 + 5 + 4 + 5)/ 19 = 4

Среднее линейное отклонение (|6-4| + |5-4| + |3-4| + |2-4| + |4-4| + |4-4| + |2-4| + |3-4| + |3-4| + |5-4| + |6-4| + |2-4| + |7-4| + |2-4| + |5-4| + |3-4| + |5-4| + |4-4| + |5-4|)/19 = 1,3

Верхняя граница = 4 + 1,3 = 5,3

Нижняя граница = 4-01,3 = 2,7

Показатели, вошедшие между верхней и нижней границами, относятся к среднему уровню.

Полученные результаты позволяют нам сделать следующие выводы: наиболее частые ошибки, встречающиеся в заданиях на построение объяснения в устной форме по предложенному плану и в заданиях на использование таблиц, проверки по таблице. Для повышения уровня сформированности познавательных учебных действий мы разработали фрагменты занятий по применению дидактических игр на уроках математики.

Целесообразность использования дидактической игры на разных этапах урока различна. При усвоении новых знаний ее возможности уступают традиционным формам обучения. Поэтому дидактические игры чаще применяет при проверке результатов обучения, выработке навыков, формировании умений. При систематическом использовании они служат эффективным средством активизации познавательных учебной деятельности школьников [3].

Занятие 1.

Формируемое познавательное учебное действие: самостоятельно проводить сравнения, сериацию, классификацию, выбирая наиболее эффективный способ решения или верное решение.

Задание выполняется в форме дидактической игры «Коллективный счет». Класс делится на 2 варианта – группы, каждый выполняет индивидуально задания, а затем проверяют вместе.

Запишите следующие числа в порядке возрастания. (В-1)

256358975 35698712 9699697 256358969

3569872 9699997 25638969 6996979

Запишите следующие числа в порядке убывания. (В-2)

5264837 62348927 21396 4587369

98632475 2138657 458231 69371452

Занятие 2.

Формируемое познавательное учебное действие: владение общими приемами решения задач, выполнение заданий и вычислений.

Задание выполняется в виде дидактической игры «Помоги расставить числа». Работа организуется в группах, в каждой группе не менее 8 человек. Каждый участник решает пример, а затем лидер группы расшифрует слово и представляет результат.

Расшифруйте название части света, где находится подавляющее большинство высочайших вершин мира.

Е-342:3:2 + 180:6 И-32:2*10 + 160*5

З-(55*4 + 125:5):5 Р-747:9 + 103*3 + 38

Я-1000:100 + 450:90 А-48:(72:18) + 120*8

В-705 + 45:15:3 + 94 Л-836:4-12464*3

Занятие 3.

Формируемое познавательное учебное действие: подводить под понятие на основе выделения существенных признаков.

Творческое задание, которое осуществляется в ходе выполнения упражнения. Когда возникнет проблемная ситуация, они могут воспользоваться дополнительными источниками информации (энциклопедия, словарь, интернет-ресурс) для получение информации о расстоянии Земли от Солнца и числе жителей Земли.

Из перечисленных примеров выберите те, при которых используются числа класса миллиардов:

а) число жителей России,

б) число жителей Земли,

в) состояние самых богатых людей в мире,

г) расстояние от Земли до Солнца (км),

д) расстояние от Земли до Солнца (м).

Проводим беседу о том, где нам могут встретиться большие числа класса миллиардов. Слушаем учащихся и подтверждаем (опровергаем) высказанные предположения (ученики могут называть в качестве примера число звезд в галактиках, число молекул в любом живом организме, число жителей Земли, а также состояние самых богатых людей в мире, ориентируясь на то, что их называют миллиардерами).

- Рассматривая примеры из астрономии, предлагаем обратиться к словарю. Приходим к выводу, что расстояние от Земли до Солнца (около 150 млн. км) будет подходящим примером при условии выражения данного числа в метрах.

- Предлагаем самостоятельно выразить в метрах 150000000 километров.

- Проверяем на доске:

1 км = 1000 м 150 000 000 км = 1км · 150 000 000 = = 1000 м · 150 000 000 = 150 000 000 000 м

Занятие 4

Формируемое познавательное учебное действия: строить логическую цепь рассуждений. Задание, выполняется в форме игры «Угадай! какое число задумано»

Найдите закономерности и назовите пропущенные числа.

а) 15290, 15291, 15292, ….., 15294, ……., …….;

б) 40 800, 40700, ……, 40500, ……, ………;

в) 192010, 182010, 172010, …….., ………, …….;

г) 17210, 17211, 17212, ….., 17214, ……., …….;

д) 70 800, 70 700, ……, 70 500, ……, ………;

е) 193010, 183010, 173010, …….., ………, …….

После того как дети выполнили задание, отработали навык и осознали закономерность, ученикам предлагается работа в парах. Каждый ученик создает свою числовую цепочку закономерностей. Затем ученики меняются тетрадями и выполняют задание соседа. Меняются тетрадями еще раз и проверяют своего соседа по парте.

Занятие 5.

Формируемое познавательное учебное действие: владеть общими приемами решения задач, строить объяснение в устной форме по предложенному плану.

Задание выполняется в форме индивидуальной мини-игры «Поиск лишнего». Учащиеся выполняют задания в индивидуальных карточках, несколько учеников строят свое объяснение в устной форме учителю. Представлены 2 варианта решения задачи, нужно с помощью решения каждого варианта найти верный и затем записать в индивидуальную карточку.

Кусок масла в 1 кг нужно разделить на 2 части так, чтобы в одной части было на 200 г больше, чем в другой. Сколько граммов должно быть в каждой части? Какой из следующих вариантов решения является решением данной задачи?

1-ый вариант

1) 1 кг: 2 =1000:2 = 500 г

2) 500 г = 200 г = 700 г

3) 500 г – 200 г + 300 г

2-й вариант

1) 1 кг – 200 г = 1000 г – 200 г = 800 г.

2) 800 г: 2 = 400 г

3) 400 г + 200 г = 600 г.

Выполните проверку выбранного варианта решения, сопоставив его с условием. Перепишите это решение с вычислением ответа в индивидуальную карточку. Запиши ответ.

Учащиеся самостоятельно читают задачу и рассматривают схему.

Находят на схеме:

1) сумма двух величин (1 кг);

2) результат разностного сравнения этих величин (200 г).

Далее обучающиеся самостоятельно находят, что 2-й вариант является решением задачи, и поясняют каждое из действий:

1) 1 кг – 200 г = 1000 г – 200 г = 800 г – удвоенная масса меньшей величины;

2) 800 г: 2 = 400 г – масса меньшей величины;

3) 400 г + 200 г = 600 г – масса большей величины.

Просим учащихся выполнить проверку выбранного варианта решения, сопоставив его с условием.

Ожидаемый ответ:

– Условия задачи: кусок масла надо разделить на 2 части так, чтобы в одной части было на 200 г меньше, чем в другой.

– Результат решения: 400 г – масса меньшей части; 600 г – масса большей части.

– Результат разностного сравнения масс: 600 г – 400 г = 200 г – соответствует условию задачи.

Предлагаем переписать решение задачи, с пояснением, в карточку.

Занятие 6.

Формируемое познавательное учебное действия: использовать таблицу, проверять по таблице.

Ученик работает самостоятельно с и индивидуальной карточкой.

Запишите в таблицу разрядов и классов следующие числа:

– один миллион триста шестьдесят две тысячи двести восемьдесят семь;

– один миллион девяносто четыре тысячи девятьсот восемь;

– два миллиона восемь тысяч пятьсот;

– двадцать миллионов двадцать тысяч двадцать;

– девятьсот девяносто девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять.

Занятие 7.

Формируемое познавательное учебное действия: использовать таблицу, проверять по таблице. Частично творческое задание, после отработки умения, ученикам предлагается самим придумать подобное задание и предложить решить соседу по парте. На первом этапе выполнения задания, ученики работают индивидуально, затем проверяем правильность решения. После этого ученики предлагают свою сформулированную задачу своему соседу по парте и работают в парах.

Из каких двух слагаемых должна состоять сумма, чтобы её значение равнялось числу 550, а одно слагаемое было больше другого на 70.

Сами читаем задание; определяем, что перед нами задача с известным результатом разностного сравнения (на 70 больше) и значения суммы (550).

- Можно вместе с учениками выполнить краткую запись задачи в виде таблицы:

Далее учащиеся самостоятельно решают, вычисляют и записывают ответ задачи.

Даем время на выполнение задания, оказываем индивидуальную помощь нуждающимся ученикам.

Организуем проверку:

1) 550 – 70 = 480 – удвоенное меньшее слагаемое;

2) 480 : 2 = 240 – меньшее слагаемое;

3) 240 + 70 = 310 – большее слагаемое.

Ответ: сумма состоит из двух слагаемых – 240 и 310.

Сформулируйте задачу, в которой требуется найти два числа, если известно значение суммы и значение разности этих чисел. Предложи соседу по парте решить сформулированную тобой задачу.

Занятие 8.

Формируемое познавательное учебное действие: подводить под понятие на основе выделения существенных признаков.

На магнитной доске размещаются рыбки, на обратной стороне которых записаны примеры на сравнение многозначных чисел. Учитель поочередно вызывает детей к доске с каждой команды, они «ловят» (снимают) рыбку, читают пример. Все ученики, решившие пример, обозначают ответ цифрой и показывают ее учителю. Кто решит пример раньше всех, тот получит рыбку. Какая команда больше всех «наловит» рыбок (решит примеры правильно), те лучшие рыболовы.

Сравните (<, >, =) данные неравенства и решите их.

999* 1000

9876*9875

9 990 * 60 500

235728 * 237 528

235 728* 89 642

69 500*96 5070

Составьте подобные и предложите решить их другой группе, а затем проверьте.

Занятие 9.

Формируемое познавательное учебное действие: выполнять действия по заданному алгоритму.

Задание выполняется самостоятельно, на индивидуальных карточках.

Выполните умножения столбиком.

2354*47 3187*32 4823*26

Расположите полученные результаты умножения в порядке возрастания.

Занятие 10.

Формируемое познавательное учебное действие: выполнять действия по заданному алгоритму.

Задание проводиться в форме игры «Составляем римские цифры». Поделите детей на группы. Один человек из каждой группы должен вытащить из мешка столько палочек, сколько может захватить его рука. Нужно составить из палочек как можно больше римских цифр, а затем сложить их. Составленные цифры должны быть многозначными. Побеждает группа, получившая самую большую сумму.

Занятие 11.

Формируемое познавательное учебное действие: выполнять действия по заданному алгоритму.

Задание выполняется в форме игры «Пропавшие часы».

Напишите, сколько часов и минут вам необходимо в сутки: на сон, еду, учебу и все остальные дела. Переведите часы в минуты. Сколько времени в сумме занимают все ваши дела? Посчитайте, сколько минут получится, если из двадцати четырех часов, которым равны сутки, вычесть полученное вами время. Проанализируйте, куда уходят оставшиеся минуты. Сколько таких минут у вас получается в месяц и в год?

Таким образом, работа на уроке с включением дидактических игр позволяет организовать разноуровневую работу на уроке и органично вписывается в ход урока, удобна в организации, повышает самостоятельность учащихся и позволяет формировать у них умение решать задачи на доступном им уровне сложности – это совершенствует обучение решению задач учащихся начальных классов.

Такая организация самостоятельной работы над несколькими задачами помогает сильному ученику проявить свои творческие способности, а слабому дает возможность познать радость труда – найти правильный путь решения задачи, используя дифференцированную помощь с учетом индивидуальных особенностей ученика. Помимо этого, такие задания оттачивают, формируют познавательные учебные действия.