science-review.ru
Типичные ошибки вчерашних школьников
Опыт работы с первокурсниками показывает, что большинство вчерашних школьников совершает типичные ошибки, например многие ошибочно понимают силы инерции.
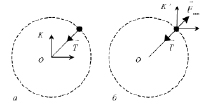
Рис. 1
Пусть тело вращается вокруг окружности (см. рис. 1) – например, грузик, привязанный к шнуру и вращающийся вокруг точки О. При наблюдении относительно инерциальной системы отсчета К (ИСО К), жестко связанный с точкой О (точкой закрепления шнура) – на частицу действует сила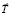 
, направленная к центру (точке O) – в данном примере это сила натяжения шнура. Под действием этой силы грузик движется по окружности. Ускорение грузика (центростремительное ускорение) постоянно направлено к центру окружности. При наблюдении относительно неинерциальной системы отсчета K' (НИСО K'), связанной с грузиком, надо учесть силу инерции 
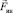– центробежную силу, которая равна по величине, но направлена против силы натяжения шнура 
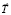. Поэтому относительно K' грузик покоится. В чем заключается традиционная ошибка обучающихся (школьников, студентов)? Они, наблюдая за вращающимся грузиком относительно K (относительно класса, аудитории…), считают, что на грузик действуют две, компенсирующие друг друга силы – сила упругости шнура и центробежная сила. В этом случае грузик по первому закону Ньютона должен был бы или покоиться, или двигаться равномерно и прямолинейно, чего, конечно, не происходит. Их ошибка заключается в том, что силу инерции нельзя учитывать относительно ИСО, она появляется лишь в НИСО!
Этому примеру аналогичен пример о спутнике, вращающемся вокруг Земли. При наблюдении за спутником, находясь на Земле, т.е. относительно ИСО K, на спутник действует лишь сила тяготения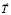 
, направленная к центру Земли и спутник вращается вокруг Земли по круговой орбите, обладая постоянным центростремительным ускорением. А при нахождении в спутнике, т.е. в НИСО K', появляется сила инерции 
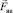, равная по величине, но направленная противоположно силе тяготения, и все тела внутри спутника, в том числе и наблюдатели, становятся невесомыми – это явление всем прекрасно известно.
В школьных учебниках физики [1–3] определение НИСО дается или словами «системы отсчета, в которых закон инерции выполняется, называются инерциальными, а те, в которых не выполняется – неинерциальными», или общеизвестными примерами с пассажиром в автобусе или сидящими в карусели. Этого недостаточно и это приводит к тем типичным ошибкам вчерашних школьников, о которых было сказано выше. Поэтому было бы желательно рассмотреть с учениками (особенно с теми, которые желают поступить физико-математические, технические и естественнонаучные направления) хотя бы некоторые из тех примеров, которые приведены ниже.
Сила инерции, появляющаяся в НИСО, движущейся прямолинейно с ускорением относительно ИСО
Любая СО, движущаяся прямолинейно-поступательно с любым (постоянным, переменным) ускорением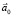 
относительно ИСО, является НИСО. В этом случае появляется сила инерции 
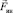, определяемая по формуле
. (2.1)
Видно, что:
1. Сила инерции появляется только в НИСО (в любой ИСО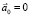 
).
2. Сила инерции всегда направлена против ускорения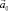 
НИСО (знак минус).
3. Сила инерции вызывает одинаковое ускорение (–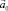 
) тел, независимо от массы, что вызывает сходство этой силы с силой тяготения, которая тоже сообщает телу одно и то же ускорение (ускорение 
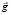свободного падения) независимо от массы. Это свойство силы инерции лучше выделить отдельным пунктом.
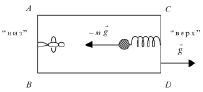
Рис. 2
4. Сила инерции и сила тяготения эквивалентны (постулат Эйнштейна). Допустим, что наблюдатель находится в закрытой, удаленной от всех внешних тел кабине, движущейся в каком-то направлении (например, направо на рис. 2) с ускорением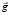 
. Тогда на все тела, находящиеся внутри кабины, будет действовать сила инерции 
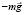, направленная налево (на рисунке). Динамометр покажет, что шарик массы m обладает «весом» mg, человек массы M почувствует свой «вес» Mg, направленный налево (на рисунке), т.е. сторона AB кабины окажется «полом», а сторона CD – «потолком». Совершенно аналогичную ситуацию можно наблюдать в неподвижной кабине, находящейся у поверхности Земли – шарик обладал бы весом mg, а человек – весом Mg (см. рис. 3). И никакими опытами, проводимыми внутри кабины, невозможно определить причину возникновения веса тел внутри кабины – ускоренным движением кабины, движущейся с ускорением g, или тяготением Земли. На этом основании можно говорить об эквивалентности сил инерции и тяготения.
Было бы исключительно полезно ознакомить учеников со следующими примерами, не требующими знаний высшей математики.
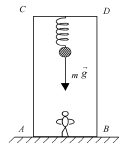
Рис. 3
Пример 1. Автобус, в котором находится пассажир, отъезжает от остановки и через 10 сек приобретает скорость 36 км/ч. Считая движение автобуса равноускоренным, определить силу инерции, действующую на пассажира.
Сила инерции по величине равна произведению массы человека M на ускорение автобуса (НИСО) a:
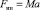
и направлена против ускорения автобуса, т.е. назад. Так как движение автобуса равноускоренное, то величина ускорения легко вычисляется:
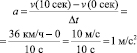
Считая массу человека равной 70 кг, нетрудно определить и величину силы инерции:
,
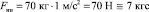т.е. на пассажира действует довольно ощутимая сила в 7 кгс, направленная назад. Это каждый чувствует на себе довольно часто.
Пример 2. Определить установившийся угол a отклонения математического маятника от вертикали, если тележка, на которой укреплен маятник, движется с ускорением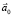 
.
Задачу можно решить относительно неподвижной ИСО и относительно НИСО, связанной с тележкой.
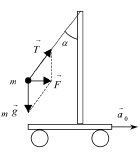
Рис. 4
А. На рис. 4 изображена тележка с маятником массы m с указанием сил, действующих на маятник – это сила тяжести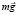 
маятника и сила натяжения нити 
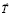, относительно ИСО. Равнодействующая 
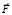этих сил, равная их векторной сумме
,
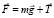действуя на маятник, сообщает ему ускорение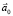 
, совпадающее с ускорением тележки (маятник относительно тележки покоится):
.
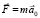Тогда искомый угол α находится из определения тангенса угла:
.
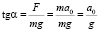Б. В случае наблюдения за маятником относительно НИСО, связанной с тележкой, необходимо учесть еще и силу инерции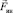 
(см. рис. 5):
.
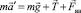Так как маятник относительно НИСО (тележки) покоится, то ускорение
,
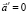а сила инерции
,
т.е.
.
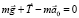Тангенс искомого угла опять, как и должно быть, дает прежнее значение:
.
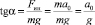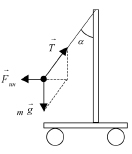
Рис. 5
Пример 3. Свободно падающий лифт. В этом случае НИСО (лифт) движется с ускорением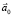 
, равным ускорению 
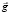свободного падения (см. рис. 6):
.
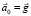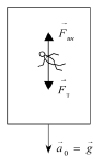
Рис. 6
Поэтому сила инерции, возникающая именно в НИСО,
,
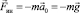равна по величине и противоположна по направлению силе тяготения
,
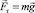и их векторная сумма равна нулю – человек (любое тело, находящееся внутри лифта) становится невесомым.
А если на это (на свободно падающий лифт) смотреть со стороны (со стороны ИСО, жестко связанной с поверхностью Земли), то на лифт (и на человека в нем) действует единственная сила – сила тяготения, и лифт, и человек падают вниз с ускорением свободного падения g.
Сила инерции, появляющаяся во вращающейся НИСО
При нахождении во вращающейся с постоянной угловой скоростью НИСО (см. рис. 7, где СО выбрана так, что вращение происходит вокруг оси Z против часовой стрелки, если смотреть сверху), вектор угловой скорости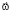 
направлен вдоль оси вращения (на рисунке вверх – направление определяется правилом правого буравчика (ППБ)). В такой вращающейся НИСО появляется сила инерции 
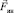, равная векторной сумме двух сил инерции:
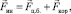(2.1)
где
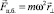(2.2)
– центробежная сила, направленная от оси вращения (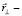
радиус-вектор частицы относительно оси вращения) и
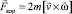, (2.3)
– кориолисова сила (сила Кориолиса), возникающая лишь для подвижного тела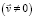 
.
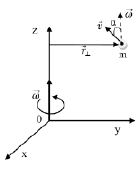
Рис. 7
По определению векторного произведения кориолисова сила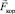 
, перпендикулярна плоскости, на которой расположены в данный момент вектор скорости 
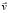тела и вектор угловой скорости 
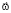вращения НИСО, а сама сила может быть выражена через определитель:
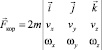. (2.4)
Но в школьной физике достаточно пользоваться другой формулой, определяющий модуль кориолисовой силы
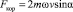, ППБ, (2.5)
а направление силы определяется правилом правого буравчика, что и указано буквами «ППБ» в формуле. Здесь α – угол между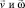 
.
Вот эти две силы инерции – центробежная сила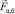 
(всегда направленная от оси вращения НИСО), определяемая формулой (2.2) и кориолисова сила 
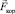, действующая на подвижное тело (направление которой постоянно меняется) и определяемая по формуле (2.5), появляются во вращающейся НИСО.
Любой школьник знает, что любой объект, жестко связанный с Землей или движущийся прямолинейно с постоянной скоростью (например, любое здание, аудитория, класс, автобус, движущийся с постоянной скоростью), является ИСО, хотя Земля, если рассмотреть строго, является НИСО и, на первый взгляд, должны быть учтены центробежная и кориолисова силы, возникающие из-за вращения Земли вокруг собственной оси и вращения Земли по определенной орбите вокруг Солнца.
В школьных учебниках [1–3] обычно пишут, что Земля (любая система отсчета, связанная с Землей) с достаточной точностью могут считаться ИСО. Эту достаточную точность можно оценить количественно [4], сравнив эти силы, например, с силой тяготения:
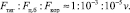(3.6)
Действительно, этими силами инерции можно пренебречь, если исследуемая задача не требует значительных точностей. Несмотря на это, именно кориолисова сила позволяет объяснить такое явление, как более сильный подмыв правых берегов рек, если смотреть вдоль течения. На рис. 8 нарисована Земля – ось АА – ось вращения Земли, угловая скорость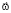 
вращения Земли направлена с юга на север (ППБ). Пусть река находится на северном полушарии Земли, и течет с юга на север (это, например, река Лена в России). На рисунке показаны скорость 
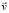течения реки на широте φ и вектор угловой скорости 
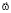вращения Земли. По ППБ ясно, что сила Кориолиса 
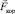будет давить на правый берег реки (это показано крестиком).
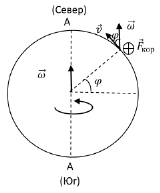
Рис. 8
Пример 4. Оценить величину силы Кориолиса для реки Лены около города Якутска.
Ширина L реки Лены около Якутска около километра, т.е., L ≈ 1 км, а широта Якутска φ = 67 °. На рис. 9 показан вид сверху на реку. Кориолисова сила, действующая на S = 1 м2 правого берега:
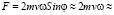
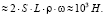
И под действием этой силы, постоянно действующей на правый берег реки, происходит более сильный подмыв правого берега.
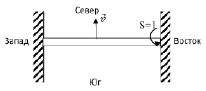
Рис. 9
Заключение
Казалось бы, всё очень просто – силы инерции появляются только в НИСО! Но нет – существенная часть вчерашних школьников этого не знает. В этом вопросе путаются даже учителя физики. Поэтому авторы так и назвали статью – «Школьная физика: силы инерции» – и обращаются именно к учителям физики, чтобы на то, что сказано в этой статье, они обратили особое внимание. Приведенные примеры не требуют знаний по высшей математике, и они по силам любому ученику.