Одним из главных факторов, определяющих будущий уровень социального и экономического развития России, является профессиональная подготовка и интеллектуальное развитие молодежи. В целях сохранения и приумножения научного и производственного потенциала страны необходимо обеспечить развитие творчески активной, склонной к научно-исследовательской деятельности, грамотной и целеустремленной личности [1].
Одной из основных проблем управления подготовкой специалистов в вузах становится прогнозируемое снижение количества и качества подготовки выпускников общеобразовательных школ и уже проявляющиеся в связи с этим трудности комплектования контингента учреждений высшего профессионального образования. Наряду с этим возникает проблема адаптации студентов младших курсов к обучению в высшем учебном заведении, преодоления ими, так называемого барьера «школа – вуз» [2].
В этих обстоятельствах одной из главных задач высшей школы становится выявление, обучение, привлечение, поощрение и поддержка профессионально-ориентированной, склонной к дальнейшему обучению молодежи. Решением такой задачи должна стать система довузовской подготовки в высших учебных заведениях. Довузовская подготовка есть синтез обучения и учения, воспитания и самовоспитания, развития и саморазвития, взросления и социализации; рассматривается как средство дифференциации и индивидуализации обучения, когда за счет изменений в структуре, содержании и организации образовательного процесса более полно учитываются интересы, склонности и способности учащихся, создаются условия для учащихся в соответствии с их профессиональными интересами и намерениями в отношении продолжения образования. При этом существенно расширяются возможности выстраивания учащимися собственной индивидуальной образовательной траектории [3].
Усиление роли дополнительного практико-ориентированного образования в развитии школьников связано с их переходом к более высокой форме учебной деятельности, в которой для учащихся раскрывается ее смысл как деятельности по самообразованию и самосовершенствованию. На первый план выдвигается стремление к овладению глубокими, настоящими знаниями, хотя бы в какой-либо ограниченной области. Поэтому участие школьников в научно-образовательных соревнованиях становится фактором личностной образовательной стратегии учащегося общеобразовательного учреждения как потенциального студента [4].
В настоящее время, когда во всех регионах ЕГЭ стал обязательным, а его результаты засчитываются как вступительные испытания в вузы, актуальным стал вопрос об альтернативных формах поступления в высшие учебные заведения. Министерство образования и науки России в качестве такой альтернативы рассматривает олимпиады школьников – тематические, предметные, научно-образовательные [3].
Предлагаемая работа является продолжением рассмотрения примеров и задач при подготовке к олимпиаде по физике для школьников [5].
Примеры задач и методов решений
Кинематика равнопеременного прямолинейного движения имеет существенное отличие по сравнению с равномерным движением. Равномерное прямолинейное движение значительно более богато на задачи, чем равнопеременное движение. Появление еще одного переменного, я имею в виду ускорение, позволяет формализовать почти 90 процентов задач [6, 7]. И это подтверждение того закона, что чем проще условие, тем сложнее задача, или чем сложнее условие, тем проще решение. Попробуем это доказать.
В кинематике равнопеременного прямолинейного движения существует единственная формула, хорошо известная со средней школы:
± H = ± H0 ± V0t ± at2?/2.
Эта формула определяет координату, но ни в коем случае не путь. Вообще, в курсе физики есть только одно упоминание формулы, определяющей путь. И она связана с разделом равномерного движения. Поэтому, как только в условии задачи появился вопрос, связанный с нахождением пути пройденным телом, будьте внимательны, сразу записать выражение для пути будет затруднительно.
Второе, на что хотелось бы обратить внимание, – это знаки в этой формуле. Их выбор определяется выбором системы отсчета при решении задачи. На всякий случай напомню, что система отсчета включает в себя материальное тело, с которым связывают систему координат, сама система координат и часы. На рис. 1 приведены правила выбора знаков для этой формулы.
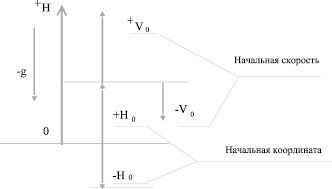
Рис. 1
Третье, и это очень важно, выбранные знаки, которые определяют вид движения рассматриваемого тела в начальный момент, остаются постоянными при дальнейшем движении. Это связано с тем, что в формуле присутствует параметр V0, который существует только для момента начала отсчета. В другое время и скорость будет другая. Для иллюстрации сказанного приведем пример типичной ошибки в следующей задаче.
Задача 1. Льдинку бросают вверх по горе так, что она начинает скользить со скоростью V0. На расстоянии S0 от точки бросания льдинка побывала дважды в моменты времени t1 и в момент t2. Определить начальную скорость тела и его ускорение.
Выбрав систему отсчета, как показано на рис. 2, задача решается довольно просто, если бы не одно но. Понятно, что тело при условии задачи в одной точке может быть дважды только при подъеме и спуске. В первом случае тело движется равнозамедленно, во втором равноускоренно. В предположении, что трение отсутствует, ускорение будет оставаться постоянным. Теперь осталось записать уравнение координаты тела для этих двух случаев. И здесь начинаются сложности.
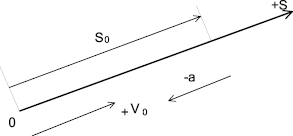
Рис. 2
Для движения вверх по горке уравнение, как правило, пишут уверенно:
S0 = V0t1 – a(t1)2/2.
А вот для случая движения тела вниз в формуле ставят знак «+», объясняя это тем, что тело движется в этот момент равноускоренно. Но правильнее писать знак минус в обоих уравнениях, для первого и второго случаев, т.к. знаки в этой формуле зависят только от начального вида движения, а оно было равнозамедленным.
S0 = V0t1 – a(t1)2/2,
S0 = V0t2 – a(t2)2/2.
Решение этой системы уравнений не вызывает трудностей.
Удачный выбор системы отсчета очень часто резко упрощает решение задачи. В качестве примера приведем следующую задачу.
Задача 2. С воздушного шара, поднимающегося вверх с некоторой скоростью, выпадает тело. Через t секунд оно падает на землю. Определить, с какой высоты упало тело. Эта задача может поставить в тупик не только абитуриента, но и опытного преподавателя. Дело в том, что выбрав как обычно систему отсчета, связанную с землей, вы получаете одно уравнение с двумя неизвестными H и V и дальше не видно пути его решения:
0 = H – V0 t – g(t)2/2.
Выход из этого тупика довольно прост. Возьмите систему отсчета, связанную с шаром, который движется вверх со скоростью V относительно земли и которая нам неизвестна. После такого выбора мы вправе остановить шар, но при этом мы вынуждены будем всем телам, которые рассматриваются в задаче, присвоить значения относительных скоростей. Как это сделать, довольно подробно описано в статье автора, посвященной равномерному движению. В нашем случае есть только одно тело, которому необходимо присвоить относительную скорость – это земля. Ее относительная скорость равна (– V0). Остановив воздушный шар, мы заставили двигаться землю, но при этом высота падения измеряется относительно шара. Время падения до земли известно и равно t, а ускорение равно g. Поэтому высота падения определится из следующего уравнения:
H = g(t)2/2.
Так как начальная скорость в нашей выбранной системе отсчета равна нулю, мы получили формулу свободного падения.
Продолжая эту тему, следует обратить внимание читателя на задачи, связанные с определением перемещения тела за одну секунду. Одна секунда – это и первая, и последняя, но при этом перемещения приходится рассчитывать по-разному. Если для первой секунды тело движется с начальной скоростью, как правило, равной нулю, то в последующих моментах времени тело будет иметь начальную скорость отличную от нуля. И при этом возникает проблема определения начальной скорости движения, и в связи с этим резко усложняется решение задачи.
Выход довольно простой. Предлагаем систему отсчета расположить в точке начала свободного падения, и это существенно облегчит решение. За примером далеко ходить не надо. Вот одно из условий задачи, которое есть почти в каждом пособии по физике.
Задача 3. Определить путь, пройденным свободно падающим телом, за первую и последнюю секунду своего падения, если известна высота падения. Выбрав предлагаемую систему отсчета, ясно, что путь и перемещение за первую секунду будут равны и их легко найти. Далее определяется все время полета, благо нам дана высота падения. Затем из полученного значения вычтем единицу, и перед нами время падения без последней секунды (кстати, это и время падения без первой секунды). Далее, определяется координата тела за время свободного падения без последней секунды. Ну, а путь за последнюю секунду определим, если вычтем из общей высоты падения полученную координату.
Можно продолжать рассматривать задачи на этот раздел кинематики, но алгоритм решений будет оставаться, как правило, тем же, поэтому перейдем к тем 10 процентам задач, алгоритм решения которых не вписывается в общую схему.
Задача 4. Из воздушного шара, опускающегося со скоростью V0 относительно земли, бросают вверх тело со скоростью V1 тоже относительно земли. Определить максимальное расстояние между телом и воздушным шаром. Чтобы определить это расстояние, мы должны понять, что тела будут сближаться только при условии, что одно из тел будет иметь скорость большую, чем у другого тела. Поэтому сначала найдем время, когда у них сравняются скорости:
– V0 = + V1 – gt.
Понятно, что система координат связана с землей, а положительная ось направлена вертикально вниз. По найденному времени нетрудно определить координаты воздушного шара и тела. А разница между ними определяет максимальное расстояние. При равнопеременном движении, как и для случая равномерного движения, полезно использовать метод относительного движения, который подробно описан в статье [8].
Задача, которая проиллюстрирует данный метод, довольно часто встречалась на Московских физических олимпиадах в той или другой интерпретации. Одно из возможных условий следующее.
Задача 5. Два тела двигаются вдоль прямой навстречу друг другу со скоростями V1 и V2 и постоянными ускорениями a1 и а2 направленные в разные стороны соответствующим скоростям. Определить, при каком максимальном начальном расстоянии L0 они могут встретиться. Решение не вызовет затруднений, если, основываясь на принципе относительного движения, остановим одно из тел. Допустим остановили первое тело, тогда второе будет двигаться со скоростью (V1 + V2), а его ускорение будет равно относительно первого тела (a1 + а2). Расстояние, которое должно пройти второе тело относительно покоящегося первого тела, при условии встречи, должно быть не меньше L0. Подставив в выражение L0 = (V1 + V2)2 / 2 (a1 + а2) данные задачи, получим значение максимального начального расстояния L0.
В заключение познакомим читателя с задачей, которая будет полезна не только абитуриентам, но и преподавателям.
Задача 6. Пассажир, спешащий на поезд, вбегает на перрон, а мимо него проходит предпоследний вагон его поезда за t1 секунд, а последний за время t2. Определить, на сколько опоздал пассажир? Считать движение поезда равноускоренным с начальной скоростью равной нулю.
При встрече с этой задачей почти всегда получаешь вопрос, сколько было вагонов или чему равна длина вагона или как звали машиниста поезда? Но этого при решении не потребуется.
Допустим, пассажир опоздал на время t0, а длина вагона равна L. Тогда начальная скорость движения предпоследнего вагона мимо пассажира будет равна: V = a(t0), где а – ускорение поезда. Вагон мимо него проходит за время t1, следовательно:
L = a(t0) t1 + at12/2.
Для последнего вагона запишем аналогично:
L = a(t0+ t1)(t2) + at22/2.
Эта система легко решается, если приравняем левые части, а ускорение сократится. Далее останется выразить одно лишь неизвестное t0.
Заключение
Организация научно-образовательных мероприятий для школьников в высших учебных заведениях становится информационным каналом, через который, кроме прочего, вузы предъявляют свои требования к подготовленности абитуриента для поступления и обучения. Реализация довузовского образования позволяет обеспечить эффективное взаимодействие учреждений среднего и высшего образования; значительно обогатить потенциал школ за счет профессорско-преподавательского состава вузов, осуществляющих сотрудничество со школами; помогает учащимся углубить процесс познания предметов, ставших объектом их научно-исследовательской работы; создает благоприятные условия для поступления в вуз; приобщает школьников к научной, исследовательской и творческой деятельности.


 science-review.ru
science-review.ru