В последнее время все чаще высказывается идея о том, что ученик должен не вообще получать образование, а достигнуть некоторого уровня компетентности в способах жизнедеятельности в человеческом обществе, чтобы оправдать социальные ожидания нашего государства о становлении нового работника, обладающего потребностью творчески решать сложные профессиональные задачи. Поэтому сегодня важно не столько дать ребенку как можно больший багаж знаний, сколько способствовать обеспечению его общекультурного, личностного и познавательного развития, создать условия для освоения такого важного умения, как умение учиться, что является главной задачей новых образовательных стандартов, которые призваны реализовать развивающий потенциал общего среднего образования.
В современной научной психологической литературе имеют место множество определений понятия «предметной компетенции». В каждом толковании этого термина есть что-то общее сближающее их все, но в то же время прослеживается и собственное видение каждого автора, отличающее все определения друг от друга. Под предметной компетенцией большинство авторов (А.В. Хуторской, И.А. Зимняя, С.Е. Шишов, Дж. Ровен и др.) понимают как специфические способности, необходимые для эффективного выполнения конкретного действия в конкретной предметной области и включающие узкоспециальные знания, особого рода предметные умения, навыки, способы мышления.
Предметная компетенция является ведущей при определении качества учебной деятельности обучающегося. Формирование предметной компетенции только тогда является успешным, когда она постоянно реализуется в учебной и практической деятельности. Лишь в том случае компетенция учащихся достигает высокого уровня сформированности, когда педагог уделяет всем необходимым действиям максимум внимания и сознания.
Методологической основой исследования выступили труды отечественных исследователей предметных компетенций – А.В. Хуторской [4], И.А. Зимняя., С.Е. Шишов [5], а также труды зарубежного исследователя – Дж. Равен [3].
Результаты исследования были внедрены в учебный процесс школ города Лесосибирска.
Использование компетентностного подхода в школьном образовании должно решить проблему, типичную для школы, когда ученики могут хорошо овладеть набором теоретических знаний, но испытывают значительные трудности в деятельности, требующей использования этих знаний для решения конкретных задач или проблемных ситуаций. При этом, одну из проблем компетентностного подхода в современной школе многие исследователи связывают с разработкой системы оценивания сформированности компетенций [1].
Математика – дисциплина с устойчивыми традициями преподавания. На уроках математики мы решаем математические проблемы, навыки, решения которых впоследствии будут способствовать решению возникающих жизненных проблем. Для того чтобы добиться успеха в жизни, в профессии от учащегося требуется почти то же, что и для успеха в математике: способность логически мыслить, изобретательность, способность выделить в условиях задачи существенную информацию.
Предметная компетенция является ведущей при определении качества учебной деятельности обучающегося. Формирование предметной компетенции только тогда является успешным, когда она постоянно реализуется в учебной и практической деятельности. Лишь в том случае компетенция учащихся достигает высокого уровня сформированности, когда педагог уделяет всем необходимым действиям максимум внимания и сознания.
Обучение учащихся в начальной школе на уроках математики направлено на развитие предметных компетенций: умение структурировать данные (ситуацию), вычленять математические отношения, создавать математическую модель ситуации, анализировать и преобразовывать ее, интерпретировать полученные результаты.
К приёмам формирования предметных компетенций на уроке математики можем отнести:
– использование межпредметных связей, которые на уроке математики формируют представления о взаимосвязях различной направленности, роли математических знаний в зависимости от других предметов;
– составление системы упражнений, направленной на формирование предметных компетенций у младших школьников на уроках математики.
Исследование проводилось среди учащихся 5 классов на базе школ г. Лесосибирска.
Наиболее удачны в практике следующие методы обучения:
1. Метод дискуссии:
– круглый стол, обсуждение.
2. Метод исследования:
– мозговой штурм;
– идеальное задание (учитель предлагает школьникам выполнить дома работу по их собственному выбору и пониманию).
3. Частично-поисковый метод:
– поиск общего;
– найди объяснения.
4. Творческий метод:
– удивляй! (учитель находит такой угол зрения, при котором даже обыденное становится удивительным);
– отсроченная отгадка! (учитель даёт удивительный факт-загадку, отгадка к которой будет открыта при работе с новым материалом);
– лови ошибку! (учитель намеренно допускает ошибку);
– посмотри чужими глазами,
– театрализация.
5. Образовательный квест [2].
Для проверки уровня сформированностипредметных компетенций у учащихся младшего школьного возраста на уроках математики мы провели констатирующий эксперимент на базе 5 класса.
Для исследования знания учащимся были предложены различные упражнения:
- упражнения на умение структурировать данные (ситуацию);
- упражнения на умение вычленять математические отношения;
- упражнения на умение создавать математическую модель ситуации;
- упражнения на умение анализировать и преобразовывать математическую модель ситуации;
- упражнения на умение интерпретировать полученные результаты.
В связи с большим объемом работы этапы экспериментального исследования были разбиты на 4 урока.
Цель констатирующего эксперимента – проверить уровень сформированности предметных компетенций у младших школьников на уроках математики.
На данном этапе учащимся были предложены упражнения, направленные на выяснение уровнясформированности предметных компетенций у учащихся младшего школьного возраста на уроках математики.
Упражнения на умение структурировать данные (ситуацию)
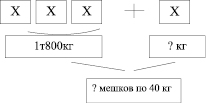
Задача 1. С одного поля собрали 1 т 800 кг картофеля, а с другого – в 3 раза меньше. Весь картофель разложили в мешки, по 40 кг в каждый. Сколько мешков с картофелем получили?
Составление схемы решения.
Задача 2. Один мастер изготовил 6 ниток бус, по 38 бусинок в каждой, а другой – 7 ниток бус, по 36 бусинок в каждой. Какой мастер использовал больше бусинок и на сколько?
Составление схемы решения:

Упражнения на умение вычленять математические отношения
Математический диктант № 1
1. Найди сумму чисел 7 699 и 5000.
2. Запиши наименьшее пятизначное число.
3. Найди третью часть от числа 720.
4. Запиши число, которое на 1 единицу больше, чем 73 899, 100 009.
5. На сколько 630 больше 400?
6. На сколько надо разделить 6000, чтобы получить 3000?
7. В городском парке 120 берёз, а клёнов на 89 больше. Сколько клёнов растёт в городском парке?
8. Найди произведение 7 и 400.
9. 70 умножить на 6, разделить на 2 и увеличить на 160.
10. На одной полке 54 книги, а на другой в 6 раз меньше. Сколько книг на другой полке?
Математический диктант № 2.
1. Оле исполнилось 12 лет. Она моложе Лены на 4 года. Найдите возраст Лены?
2. Вычислите 3400 – 324.
3. В одной пачке 24 тетради, а в другой в 3 раза больше. Сколько всего тетрадей в двух пачках?
4. Вычислите: 36 + 72 : 12 : 3.
5. Разность двух чисел равна 39, вычитаемое 13. Найдите уменьшаемое.
6. Во сколько раз 7 м меньше, 35 м?
7. Найдите произведение чисел 960 и 60.
8. Стороны прямоугольника равны 4 м и 6 м. Найдите его площадь.
9. Во сколько раз 2 700 больше, чем 9?
10. На сколько надо уменьшить 420, чтобы получить 60?
Упражнения на умение создавать математическую модель ситуации
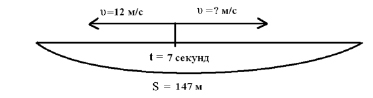
Задача 1. От одного места одновременно в противоположных направлениях побежали 2 собаки. Через 7 секунд расстояние между ними было 147 м. Скорость одной собаки 12 м/с. Какова скорость второй собаки?
Составление математической модели:
Решение:
1) 147 : 7 = 21 (м/с) – общая скорость 2-х собак
2) 21 – 12 = 9 (м/с) – скорость 2-й собаки
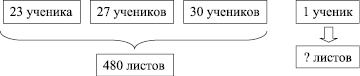
Задача 2. По сколько листов бумаги на ученика купил каждый из трех учителей, если у одного 23 учеников, у другого 27 учеников, у третьего 30 учеников? Всего тремя учителями было куплено 480 листов бумаги, на каждого ученика равное количество листов.
Составление математической модели:
Решение:
1) 23 + 27 = 50 (уч.) – у 2-х учителей
2) 50 + 30 = 80 (уч.) – всего
3) 480 : 80 = 6 (л) – у каждого ученика
Упражнения на умение анализировать и преобразовывать математическую модель ситуации
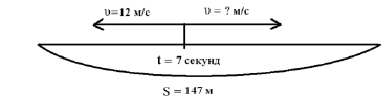
Задача 1. От одного места одновременно в противоположных направлениях побежали 2 собаки. Через 7 секунд расстояние между ними было 147 м. Скорость одной собаки 12 м/с. Какое было бы расстояние между собаками, если бы они бежали в одном направлении?
Составление математической модели:
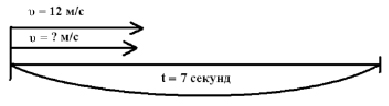
Решение:
1) 147 : 7 = 21 (м/с) – общая скорость 2-х собак
2) 21 – 12 = 9 (м/с) – скорость 2-й собаки
3) 12 * 7 = 84 (м) – пробежала 1 собака
4) 9 * 7 = 63 (м) – пробежала 2 собака
5) 84 – 63 = 21 (м) – расстояние между собаками
Задача 2. Сколько листов бумаги купил каждый из трех учителей, если у одного 23 учеников, у другого 27 учеников, у третьего 30 учеников? Всего тремя учителями было куплено 480 листов бумаги, на каждого ученика равное количество листов.
Решение:

Решение:
1) 23 + 27 = 50 (уч.) – у 2-х учителей
2) 50 + 30 = 80 (уч.) – всего
3) 480 : 80 = 6 (л) – у каждого ученика
4) 23 * 6 = 138 (л) – купил 1 учитель
5) 27 * 6 = 162 (л) – купил 2 учитель
6) 30 * 6 = 180 (3) – купил 1 учитель
После проведения предложенных заданий у нас получились следующие результаты (табл. 1).
Таблица 1
Результаты диагностики сформированности предметных компетенций у младших школьников
|
Ф. И. ученика |
Задание 1 |
Задание 2 |
Задание 3 |
Задание 4 |
Задание 5 |
Кол-во баллов |
|
1. Петр А. |
+ |
+ |
+ |
– |
+ |
4 |
|
2. Ольга Б. |
+ |
+ |
– |
+ |
– |
3 |
|
3. Александра Д. |
– |
– |
+ |
– |
– |
1 |
|
4. Виктор Д. |
+ |
– |
– |
– |
– |
1 |
|
5. Сергей Д. |
+ |
+ |
– |
– |
– |
2 |
|
6. София И. |
– |
– |
+ |
+ |
+ |
3 |
|
7. Егор К. |
– |
+ |
– |
– |
– |
1 |
|
8. Лена К. |
– |
– |
+ |
+ |
– |
2 |
|
9. Валерий К. |
+ |
+ |
– |
– |
– |
2 |
|
10. Алексей К. |
+ |
+ |
– |
+ |
– |
3 |
|
11. Дмитрий К. |
+ |
+ |
+ |
– |
+ |
4 |
|
12. Анна М. |
+ |
– |
– |
– |
– |
1 |
|
13. Андрей М. |
+ |
+ |
+ |
+ |
+ |
5 |
|
14. Лада П. |
– |
+ |
– |
– |
– |
1 |
|
15. Мария С. |
– |
+ |
+ |
+ |
+ |
4 |
|
16. Кирилл С. |
+ |
– |
+ |
– |
– |
2 |
|
17. Ольга У. |
+ |
+ |
– |
+ |
– |
3 |
|
18. Надя Ф. |
+ |
+ |
– |
– |
– |
2 |
|
19. Зарина Ч. |
+ |
+ |
+ |
– |
– |
3 |
Анализируя полученные результаты, мы пришли к следующим выводам: с первым заданием справились многие учащиеся – 13 человек из 19 (это 68 % учащихся). Со вторым заданием справились также 13 человек (68 % учащихся). С третьим заданием справилось намного меньше – 9 человек из 19 (это 47 % учащихся). С четвертым заданием справились всего 7 человек (это 37 % учащихся). С пятым заданием справились меньше всего учащихся – 5 человек (это 26 % от всего класса). Результаты представлены на рис. 1.
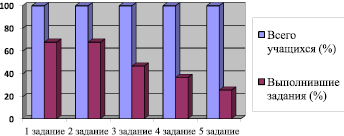
Рис. 1. Результаты диагностики сформированности предметных компетенций у младших школьников
Таблица 2
Результаты диагностики уровня сформированности предметных компетенций у младших школьников
|
Ф. И. ученика |
Кол-во баллов |
Уровень сформированности предметных компетенций |
|
1. Петр А. |
4 |
средний |
|
2. Ольга Б. |
3 |
средний |
|
3. Александра Д. |
1 |
низкий |
|
4. Виктор Д. |
1 |
низкий |
|
5. Сергей Д. |
2 |
низкий |
|
6. София И. |
3 |
средний |
|
7. Егор К. |
1 |
низкий |
|
8. Лена К. |
2 |
низкий |
|
9. Валерий К. |
2 |
низкий |
|
10. Алексей К. |
3 |
средний |
|
11. Дмитрий К. |
4 |
средний |
|
12. Анна М. |
1 |
низкий |
|
13. Андрей М. |
5 |
высокий |
|
14. Лада П. |
1 |
низкий |
|
15. Мария С. |
4 |
средний |
|
16. Кирилл С. |
2 |
низкий |
|
17. Ольга У. |
3 |
средний |
|
18. Надя Ф. |
2 |
низкий |
|
19. Зарина Ч. |
3 |
средний |
Условные обозначения: Высокий уровень – 5 баллов; Средний уровень – 3–4 балла; Низкий уровень – 1–2 балла.
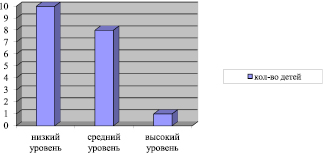
Рис. 2. Распределение учащихся по уровню сформированности предметных компетенций
Для выявления высокого, среднего и низкого уровней изучаемых показателей следует применить следующие формулы:
верхняя граница = М + ?d,,
нижняя граница = M – ? d,
где М – среднее арифметическое, d – среднее линейное отклонение.
Среднее линейное отклонение рассчитывается по формуле
Среднее линейное отклонение = 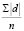 ,
,
где Σ (сигма) – сумма; |d| – абсолютное значение каждого индивидуального отклонения от средней арифметической; n – число данных в ряду.
Среднее арифметическое:
(4 + 3 + 1 + 1 + 2 + 3 + 1 + 2 + 2 + 3 + + 4 + 1 + 5 + 1 + 4 + 2 + 3 + 2 + 3)/ 19 = 2,5.
Среднее линейное отклонение
(|4-2,5| + |3-2,5| + |1-2,5| + |1-2,5| + |2-2,5| + |3-2,5| + |1-2,5| + |2-2,5| + |2-2,5| + |3-2,5| + |4-2,5| + |1-2,5| + |5-2,5| + |1-2,5| + |4-2,5| + |2-2,5| + |3-2,5| + |2-2,5| + |3-2,5|)/19 = 0,5/19 = 0,1.
Верхняя граница = 2,5 + 0,1 = 2,6.
Нижняя граница = 2,5-0,1 = 2,4.
Полученные результаты позволяют нам сделать следующие выводы: что недостаточно сформированы умения создавать математическую модель ситуации; умения анализировать и преобразовывать математическую модель ситуации; умения интерпретировать полученные результаты.
Нами разработаны методические рекомендации по формированию предметных компетенций у младших школьников на уроках математики. Представим несколько фрагментов урока с использованием предложенных приемов, для формирования предметных компетенций у детей младшего школьного возраста на уроках математики.
Фрагмент урока № 1
Удивляй! (учитель находит такой угол зрения, при котором даже обыденное становится удивительным).
Тема урока – Масса (повторение). Этап урока – Актуализация знаний.
– Ребята, что мы проходили на прошлом уроке? (единицу измерения массы)
– Молодцы, тогда вы помните, в чем массу измеряют? (в кг)
– Хорошо, тогда скажите-ка, что тяжелее – килограмм гвоздей, или килограмм ваты? (…) Почему?
– Одинаково. Почему? (килограмм есть килограмм)
Фрагмент урока № 2
Отсроченная отгадка! (учитель даёт удивительный факт-загадку, отгадка к которой будет открыта при работе с новым материалом)
Тема урока – Примерное измерение площади. Этап урока – Актуализация знаний.
– Ребята, скажите, пожалуйста, помните ли вы, что такое площадь? (величина, показывающая, сколько места занимает фигура на плоскости)
– Хорошо. В чем измеряется площадь? (в м2, см2, мм2,…)
– Вы правы. А кто помнит, как найти площадь фигуры? (ширину умножить на длину)
– Верно. Ну, раз вы уже все знаете, тогда вы без труда найдете площадь данных фигур.
На доске нарисованы фигуры:
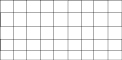
а)
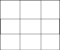
б)
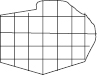
в)
– Давайте проверим, что у нас получилось? (…)
– Почему мы не смогли найти площадь фигуры под буквой в)?(…)
– Сегодня мы с вами научимся находить площадь данной и похожих фигур.
Фрагмент урока № 3
Круглый стол, обсуждение
Тема урока – Измерение и дроби. Этап урока – Изучение нового материала.
(дети разделены на 4 группы)
– Ребята, посмотрите на доску (проектор). Что там изображено? (поле с цветами)
– Какие цветы растут на этом поле? (ромашки, васильки, одуванчики)
– Хорошо. Как вы думаете, чего растет на поле больше? (ромашек).
– А как вы определили? (…)
– Посмотрите внимательно, что необычного вы замечаете? (поле разделено на квадратики)
– Верно. А теперь поработайте в группах. Посчитайте сколько всего квадратиков на этом поле? (…) Сколько квадратиков занимают каждые из представленных цветов? (…)
– А теперь представьте что поле – это целый объект. Сколько частей занимает каждое растение от этого целого? (…)
– Подумайте, посовещайтесь. Как вы думаете, как это можно записать? (…)
– Откройте стр. 57. Прочитайте. Верно, ли вы записали?
– Молодцы. Как называются части получившегося у вас числа? Что эти числа обозначают? (…)
Фрагмент урока № 4
Лови ошибку! (учитель намеренно допускает ошибку);
Тема урока – Нахождение части от числа. Этап урока – Закрепление.
– Сегодня мы с вами узнали, как найти часть от числа. И для того, чтобы закрепить полученные знания, решим еще пару заданий.
Задача 1. У меня было 60 руб.; 1/3 этих денег я израсходовал на покупку книг. Сколько стоили книги?
Решение:
60 : 3 * 1 = 20 (руб.)
Задача 2. Поезд должен пройти расстояние между городами А и В, равное 300 км. Он уже прошёл 2/3 этого расстояния. Сколько это составляет километров?
Решение:
300 : 3 * 2 = 200 (км)
Задача 3. В городе 1200 домов, из них 3/4 кирпичных, остальные деревянные. Сколько всего кирпичных домов?
Решение:
1200 : 3 * 4 = 1600 (домов)
– У всех получилось так же? (нет)
– Почему? (на доске ошибка)
– В чем она заключается? (чтобы найти часть от числа, нужно число делить на знаменатель и умножать на числитель)
– Верно. На доске затаилась ошибка. Кто хочет пойти и исправить ее? (…)
– Молодцы, вы хорошо справились с заданиями.
Фрагмент урока № 5
Идеальное задание (учитель предлагает школьникам выполнить дома работу по их собственному выбору и пониманию)
Тема урока – Приближенное вычисление площадей. Этап урока – Закрепление.
– Посмотрите на доску. Что это? (пример, уравнение). Давайте попробуем определиться, пример или уравнение? (…)
Х – 128 * 84 : (6040 – 5848) * 370 + + 53878 * 0 = 69 692
– Как вы думаете, как можно найти значение Х? (…, выполнить действия наоборот)
– Верно. Для того чтобы решить данный пример, нужно выполнить все действия в обратном порядке. Кто хочет попробовать решить у доски? (…)
Хорошо. А теперь запишите домашнее задание.
– Составить пример, решаемый таким же способом, как и у примера, решенного вам самостоятельно.
Фрагмент урока № 6 («Посмотри чужими глазами»)
Тема урока – Оценка произведения. Этап урока – Работа над новым материалом.
– Ребята, посмотрите на доску. Здесь представлено задание. Попробуйте его решить (…)
Задание 1. Перед Вами девять маленьких квадратов, образованных двадцатью четырьмя спичками. Уберите 8 спичек, не трогая остальных, чтобы осталось всего лишь 2 квадрата.

Задание 2. Необходимо переложить четыре любые спички из шестнадцати, чтобы получилось три произвольных квадрата.

– Прочитайте задания внимательно, проверьте и поменяйтесь тетрадями. (…)
– Внимательно сравните и проверьте выполненную работу соседа. Все ли получилось так же как у вас? Если вы обнаружили ответы, не схожие с вашими, подумайте, почему ваш сосед ответил именно так? (…)
Задание 1 (решение).

или

Задание 2 (решение).
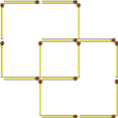
или
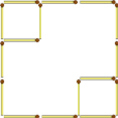
– Посмотрите, верен ли ответ вашего соседа? А ваш? (…)
Таким образом, предложенные методические рекомендации могут быть использованы учителями и студентами-практикантами при составлении уроков, а также на факультативах, так как они способствуют формированию предметных компетенций у детей младших школьников на уроках математики.


 science-review.ru
science-review.ru