science-review.ru
Людям часто приходится сталкиваться с проблемой, когда нужно подсчитать число всех возможных способов расположения предметов и исхода какого-либо события. Человеку требуется находить всевозможные варианты, которые в последующем складываются в самые различные комбинации. С поиском комбинаций такого рода приходится иметь дело представителям многих профессий. Например, логисту, при составлении расписания движения, учителю, при назначении дежурств в классе, химику, выбирающему из многих комбинаций химических элементов наилучшую.
С задачами комбинаторики людям приходилось сталкиваться еще в глубокой древности. Дальнейшее развитие комбинаторики произошло в связи с появлением таких игр как: шашки, домино и шахматы. Для оценки шанса на победу, опытные игроки применяли технику вычисления общего количества ходов, включая как положительные, так и отрицательные исходы. В результате создавался набор комбинаций, которые способствовали увеличению вероятности выигрыша. В математической науке исследования такого рода представляют особую дисциплину – теорию вероятностей, рассчитать которую без комбинаторики будет крайне затруднительно [1, 2].
В настоящие время комбинаторика получила обширное распространение и имеет огромное значение во всевозможных областях жизнедеятельности. С комбинаторными величинами сталкиваются представители многих профессий: ученый – химик, биолог, конструктор, диспетчер, астролог, экономист. Тенденция усиления интереса к комбинаторике обуславливается бурным развитием кибернетики и вычислительной техники. Понятие комбинаторика представляет собой раздел математики, базирующийся на изучении всевозможных сочетаний, перестановок, размещений, перечислений тех или иных элементов. Главная задача комбинаторики состоит в выборе правильной комбинаторной конфигурации, которая определяет метод возведения конкретной конструкции из элементов исходного множества. Примерами комбинаторных конфигураций являются блок-схемы и латинские квадраты, факториалы [3].
В книге Джеймса Андерсона «Дискретная математика и комбинаторика» выделяют следующие основные операции и связанные с ними задачи комбинаторики:
1) образование упорядоченных множеств, составление перестановок;
2) образование подмножеств, путем составления сочетаний;
3) образование упорядоченных подмножеств – составление размещений.
Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.
Множество является упорядоченным, если каждому его элементу соответствует некоторое число от 1 до n, где n – число элементов множества.
Рассмотрим правила сложения и умножения в комбинаторике [4].
Правило суммы. Если два действия A и B взаимно исключают друг друга, причем действие C можно выполнить m способами, а B – n способами, то выполнить одно любое из этих действий (либо A, либо B) можно n + m способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
.
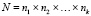Раскроем такие виды соединения как сочетания без повторений и сочетания с повторениями.
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов? [3]
.
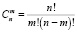Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m из этих предметов?
.
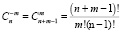Сочетание играет важную роль в математической науке, очень часто оно используется в биноме Ньютона.
Бином Ньютона – формула разложения натуральной степени двучлена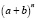 
в многочлен. Многочлены, являющиеся суммой двух слагаемых, называются биномами. Их можно представить в следующем виде:
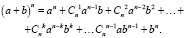
Неотрицательные целые числа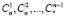 
называются биномиальными коэффициентами [5].
Формула была выведена английским математиком Исааком Ньютоном для общего случая, когда показатель степени будет произвольным, комплексным или же действительным числом.
Определить значения биномиальных коэффициентов для любой степени можно с помощью таблицы, которая получила название треугольника Паскаля.
В комбинаторике также используется факториал, который определяет натуральное число n как произведение всех натуральных чисел от 1 до n и задается следующей формулой:
.
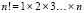Для примера вычислим факториалы 4 и 6 [6, 7]
Решение:
4! = 1*2*3*4 = 24
6! = 1*2*3*4*5*6 = 720
Рассмотрим такие виды соединения как размещения без повторений и размещения с повторениями.
Задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Еще одной составляющей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
.
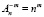Рассмотрим перестановки без повторений и перестановки с повторениями.
Задачу о числе перестановок без повторения можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
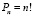
Для случая, когда среди выбираемых n элементов есть одинаковые, задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.
Рассмотрим на конкретных практических примерах как работают некоторые правила в комбинаторике [8].
Пример № 1. В магазине подарков в преддверии Нового года проходит акция: 2 набора конфет по цене одного. Маша и Настя решили воспользоваться этим специальным предложением. Им необходимо выбрать 4 из 10 имеющихся различных наборов. Сколькими способами это можно сделать?
Решение. Из 10 наборов конфет нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, применяя правило комбинаторики, а именно, сочетания без повторений, нужно найти число сочетаний из 10 элементов по 4:
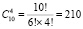
Ответ: 210 способов.
Таким образом, комбинаторика может быть применена в различных сторонах нашей повседневной жизни. Так, к примеру, мы сталкиваемся с данным понятием даже в лингвистике при рассмотрении вариантов комбинации букв, перетекающих в слова. Высокие технологии помогают применять комбинаторику даже в медицине, при расшифровке кода ДНК, выявляя таким путем наследственную предрасположенность человека к определенным заболеваниям. Но все же главной родоначальной областью применения комбинаторики является математика, поскольку сам термин был введен в математический обиход еще немецким философом Г.Ф. Лейбницем, который в 1666 году закрепил само понятие «комбинаторика» в своем фундаментальном труде «Рассуждения о комбинаторном искусстве». Более того, отдельные элементы комбинаторики, осуществляющие различные функции, играют существенную роль в экономической практике. Для решения важных экономических задач, специалисты часто применяют математическую модель анализа различных ситуаций. Методы комбинаторики используются для нужд управления, планирования, бухгалтерского учета, статистики и экономического анализа. Они позволяют решить сложные проблемы экономического развития как на микро-, так и на макроуровнях. Путем комбинации различных данных, мы можем, на примере конкретного предприятия, рассчитать вероятность возникновения рисков, связанных с понесением убытков, потерей бизнеса и деловой репутации [9].
Людей, занимающихся анализом и расчетно-экономической деятельностью, называют аналитиками. Они могут рассчитать потенциальные возможности той или иной фирмы посредством использования свойств комбинаторики. Специалисты проводят мониторинг рынка, выявляют уровень цен и конкурентоспособность отдельно взятого хозяйственного субъекта. Аналитики занимаются сбором ценной информации и выявляют дальнейшие тенденции изменений на рынке. Множество финансовых учреждений на сегодняшний день зачастую просто нуждаются в аналитиках, поскольку они делают прогнозы на стоимость ценных бумаг, драгоценных металлов, недвижимости, а также таких важных социально-экономических проблем, таких как: уровень безработицы в стране, инфляция. Таким образом, важнейшие элементы комбинаторики, состоящие из расчетно-аналитической работы, статистики, вероятностного наступления какого-либо события, позволяют вовремя выявлять существенные экономические проблемы и предотвращать их возникновение в будущем.
Библиографическая ссылка
Ледовская Я.О., Щёкина Е.О. СОВРЕМЕННЫЕ НАПРАВЛЕНИЯ ПРИМЕНЕНИЯ ЗАДАЧ КОМБИНАТОРИКИ // Научное обозрение. Педагогические науки. – 2019. – № 4-3. – С. 64-67;URL: https://science-pedagogy.ru/ru/article/view?id=2121 (дата обращения: 19.04.2024).